自动驾驶(六十九)---------降维PCA、LDA
自动驾驶是一个系统工程, 不可能有一种方法包打天下, 它是由很多子功能配合而成, 这就要求我们对其他机器学习算法都能了解, 之前在视觉中有一些很好的方法, 这里也想整理出来, 供大家参考.
在深度学习之前, 特征提取是很重要的技术, 在这中间 主成分分析(PCA)经常出现, 主题模型算法(LDA)也类似, 这里系统的总结一下:
1. 主成分分析(PCA)
在大数据时代, 最不缺的就是数据, 所以数据降维是数据处理最重要的方式, 降维在简化分析的数据同时, 希望减少降维导致的信息损失,如何实现这一目标呢? 这里我介绍一种方法 主成分分析.
PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分. 那么问题转化为如何选择K维坐标, 使得信息损失最小. 在信号处理中认为信号具有较大的方差,噪声有较小的方差,信噪比就是信号与噪声的方差比,越大越好。样本在u1上的投影方差较大,在u2上的投影方差较小,那么可认为u2上的投影是由噪声引起的。因此我们认为,最好的k维特征是将n维样本点转换为k维后,每一维上的样本方差都很大。
![]()
1. 前面介绍了方差最大化, 在一维数据中我们很好求方差, 在多维数据中需要用到协方差:
其中二维协方差: ![]()
三维协方差:![]()
2. 介绍完方差概念之后,下一个要解决的问题是如何构建两两正交的坐标轴,这就要用到线性代数的知识。
如果一个向量v是矩阵A的特征向量,将一定可以表示成下面的形式:![]()
λ是特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。
对于矩阵A,有一组特征向量v,将这组向量进行正交化单位化,就能得到一组正交单位向量。特征值分解,就是将矩阵A分解为如下式:![]() 其中,Q是矩阵A的特征向量组成的矩阵,则是一个对角阵,对角线上的元素就是特征值。
其中,Q是矩阵A的特征向量组成的矩阵,则是一个对角阵,对角线上的元素就是特征值。
3. 基于特征值分解协方差矩阵实现PCA算法步骤如下:数据集![]() ,需要降到k维。
,需要降到k维。
- 3.1 去平均值(即去中心化),即每一位特征减去各自的平均值,使得数据的期望为零。
- 3.2 计算协方差矩阵
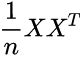 ,注:这里除或不除样本数量n或n-1,其实对求出的特征向量没有影响。
,注:这里除或不除样本数量n或n-1,其实对求出的特征向量没有影响。 - 3.3 用特征值分解方法求协方差矩阵
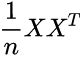 的特征值与特征向量。
的特征值与特征向量。 - 3.4 对特征值从大到小排序,选择其中最大的k个。然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P。
- 3.5 将数据转换到k个特征向量构建的新空间中,即Y=PX。从而实现了把数据从n维降低到k维。
2. 主题模型(LDA)
主题模型是用来在一系列文档中发现 抽象主题 的一种统计模型。直观来讲,如果一篇文章有一个中心思想,那么一定存在一些特定词语会出现的比较频繁。
这个过程好比我们在写文章:一般我们写文章的时候都是先给自己的文章定一个主题,然后我们会根据这个主题,用和这个主题有关的词语进行组合最后形成文章。
LDA 其实有两种含义,一种是线性判别分析, 为后续的分类问题做数据的降维处理;另一种 隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA),是一种概率主题模型。
开始时,先随机给和赋值(对所有的d和t),相当于是先验值。然后:
- 1. 针对一个特定的文档ds中的第i个单词wi,如果令该单词对应的topic为tj,可以把上述公式改写为Pj(wi|ds) = P(wi|tj)*P(tj|ds)
- 2. 枚举T中的topic,得到所有的Pj(wi|ds)。然后可以根据这些概率值结果为ds中的第i个单词wi选择一个topic。最简单的方法是取令Pj(wi|ds)最大的tj(注意,这个式子里只有j是变量)
- 3. 然后,如果ds中的第i个单词wi在这里选择了一个与原先不同的topic(也就是说,这个时候i在遍历ds中所有的单词,而tj理当不变),就会对和有影响了,它们的影响又会反过来影响对上面提到的P(w|d)的计算。对D中所有的d中的所有w进行一次P(w|d)的计算并重新选择topic看做一次迭代。这样进行n次循环迭代后,就会收敛到LDA所需要的结果了
具体推导如下:
1. 共轭分布和共轭先验:前边说贝叶斯派中,后验概率 ∝ 先验概率 × 似然函数。如果说,先验概率和后验概率在形式上是相同的,那么就可以说二者是概率共轭的关系。
2. gamma函数:这个函数本质上就是阶乘函数在实数上的推广。对于整数而言,阶乘函数:![]() ,形式如1×2×3×4×...n-1对于实数而言,不能用上述公式进行计算,阶乘函数为:
,形式如1×2×3×4×...n-1对于实数而言,不能用上述公式进行计算,阶乘函数为:![]()
3. 二项分布:对于结果的取值只有两种情况,可以认为这两种情况就是0-1。其中取值为0的概率为p,取值为1的概率为1-p。那么对于n次独立实验来说,![]() p.s.只做一次实验,是伯努利分布;重复做n次,就是二项分布。
p.s.只做一次实验,是伯努利分布;重复做n次,就是二项分布。
4. 多项分布:把二项分布扩展到多维的情况,也就是说对结果的取值不是只有两种,而是有n多种可能的取值。
就是将pLSA的基础上加了层贝叶斯框架,即LDA就是pLSA的贝叶斯版本。这个贝叶斯框架就体现在狄利克雷先验分布上。
在前边的pLSA模型中,没用什么先验分布,直接认为是个随机过程。这贝叶斯派那帮人简直不能忍啊,这不科学啊,应该有先验分布的啊,不能不按套路啊,所以这帮人就在那两个骰子参数上加上个先验分布,把这个pLSA改造成一个贝叶斯过程。这里用到的先验分布就是狄利克雷分布。根据前边说的文档的生成过程,现在可以把文档的生成抽象成如下几个问题:
- 1)从狄利克雷分布α中抽样,生成文档d的主题分布θ
- 2)从主题的多项式分布θ中抽样,生成文档d的第i个词的主题zi
- 3)从狄利克雷分布β中抽样,生成主题zi对应的词语分布φi
- 4)从词语的多项式分布φi中采样,最终生成词语wi