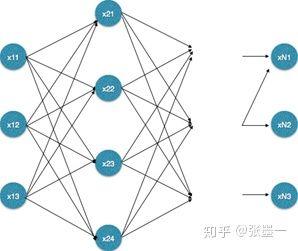
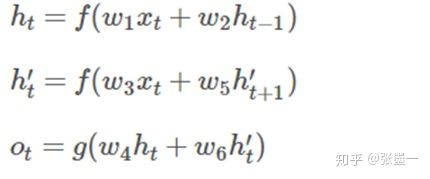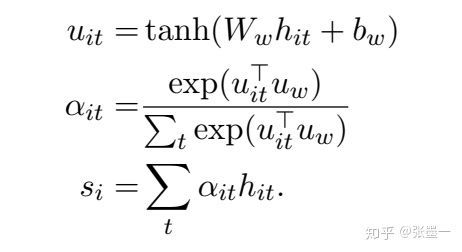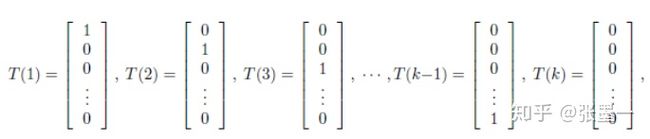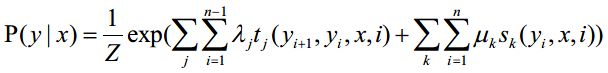LSTM+CRF机器学习模型

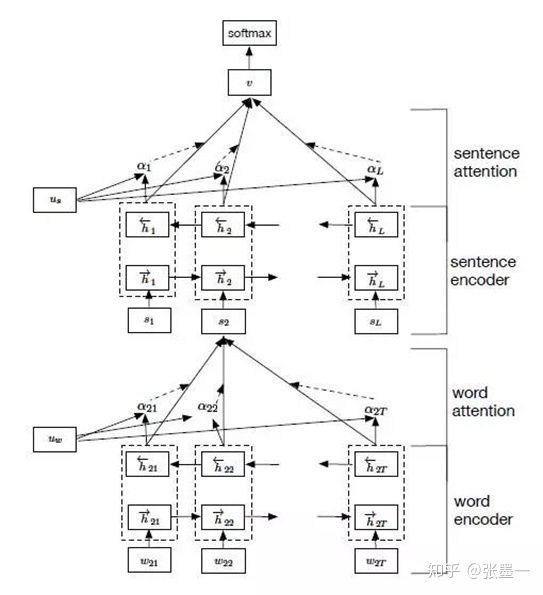
本文介绍的深度学习模型来自Di Jin和Peter Szolovits的paper《PICO Element Detection in Medical Text via Long Short-Term Memory Neural Networks》。在该模型中涉及到的知识点主要有词嵌入（word embedding）,双向LSTM网络，Attention机制（Hierarchical Attention），Softmax回归，以及条件随机场。该模型的架构如图所示。

1. word Embedding

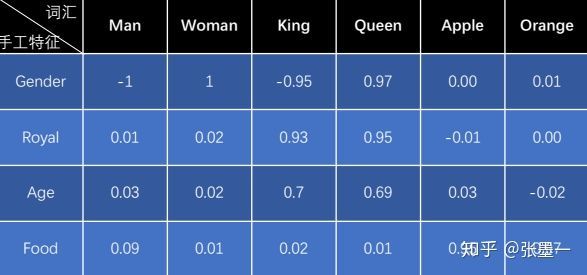
举个例子，下表词汇表在手工特征中的编码值，大小在[-1，+1]之间。绝对值越接近1表示该词具有该特征。

这里King位于词汇表的第3个位置，则King的One-hot编码为:  。

想要获得King的特征值向量，可以通过将上表表示的矩阵与King的One-hot编码做乘法得到，即  。

2. bi-Long Short-Term Memory（bi-LSTM）

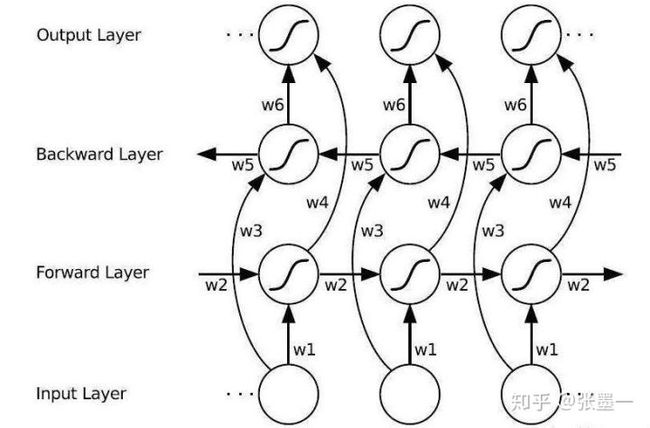
LSTM神经网络架构是RNN架构的变体。首先看一下双向的RNN展开图的架构。

该架构的输入输出可由下式给出：

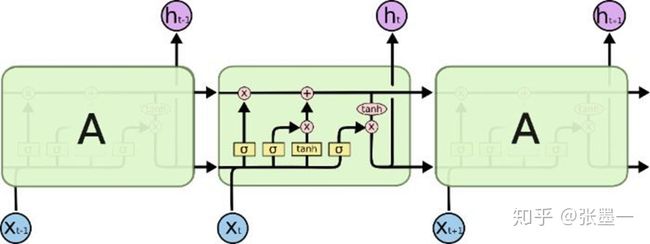
LSTM神经网络单元较RNN单元来说，增加了较多的参数。其单元内部结构如下图所示：

双向的LSTM架构则是以LSTM单元按照前面双向RNN架构的方式组织在一块的。关于各个门的输出情况，已经在《深度学习综述》一文中给出。

3. Attention机制

本模型中只使用了Hierarchical Attention模型中的Word Attention。Hierarchical Attention模型如下图所示。对于上下文关系，这里面没有使用sentence attention层，而是使用了条件随机场模型。

Why Word Attention ？

并非所有的词都对句子意义的表示有同等的贡献。因此，我们引入注意机制来提取对于句子的意义重要的词，并将这些词汇的表示聚合在一起形成一个句子向量。

How Word Attention ？

其中，  是一个随机初始化的上下文向量，会随着模型的训练一起学习。这里，Attention Pooling层首先有一个单层的神经网络将  转换成  ,通过比较  和  的相似性确定其权重。对  加权求和得到句子信息向量  。

 

4. Softmax层的数学依据

这里，首先需要对指数族分布和一般线性模型有所了解。

指数族分布：概率分布满足 

伯努利分布，高斯分布，泊松分布，贝塔分布都属于指数分布。

一般线性模型要点：

1） y|x; θ 满足一个以η为参数的指数分布，那么可以求得η的表达式。

2） 给定 x，我们的目标是要确定T(y)，大多数情况下T(y) = y，那么我们实际上要确

定的是h(x)， 而h(x) = E[y|x]。

3）  。

使用单层神经网络Softmax回归对句子进行多元分类。多元分类的对应于多项式分布，就像二元分类对应伯努利分布一样，都有其数学模型在里面。对于二元分类问题我们使用的是logistic回归。

在对数回归时，采用的是伯努利分布，伯努利分布的概率可以表示为：

其中，令  则有 

该表达式就是logistic回归的sigmoid函数。

再看Softmax回归，其 T(y)为一组k-1维的向量。

其中，  。  表示T(y)的第i个数。

求得： 

5. 条件随机场（conditional random field, CRF）

不同于隐马尔科夫模型和马尔科夫随机场这种生成式模型，条件随机场是判别式模型。

生成式模型直接对联合分布进行建模，而判别式模型则是对条件分布进行建模。

条件随机场试图对多个变量在给定观测值后的条件概率进行建模。

若令  为观测序列，  为与之对应的标记序列，则条件随机场的目标是构建条件概率模型P(y | x)。

链式条件随机场（chain-structured CRF）

 是定义在观测序列的两个相邻标记位置上的转移函数，用于刻画相邻标记变量之间的相关关系以及观测序列对他们的影响。

 是定义在观测序列的标记位置i上的状态特征函数，用于刻画观测序列对标记序列的影响。

 ，  是参数，Z是规范化因子。

这里需要对  取最大值以获取概率最大的序列，可采用维特比算法。

x_ij表示状态x_i 的第j种可能的值

#1. 从S点出发，对于第一个状态  的各个节点，计算 出S到他们的距离d（S，  ）,其中  表示任意状态1的节点。

#2. 对于第二个状态  ,的所有节点，计算出从S到它们的最短距离：

#3. 按照步骤2的方法从状态2走到状态n。