改善深层神经网络:超参数调试、正则化以及优化 第一周作业3
神经网络反向传播过程中的梯度数值逼近/梯度检查
Gradient Checking
Welcome to the final assignment for this week! In this assignment you will learn to implement and use gradient checking.
You are part of a team working to make mobile payments available globally, and are asked to build a deep learning model to detect fraud–whenever someone makes a payment, you want to see if the payment might be fraudulent, such as if the user’s account has been taken over by a hacker.
But backpropagation is quite challenging to implement, and sometimes has bugs. Because this is a mission-critical application, your company’s CEO wants to be really certain that your implementation of backpropagation is correct. Your CEO says, “Give me a proof that your backpropagation is actually working!” To give this reassurance, you are going to use “gradient checking”.
2) 1-dimensional gradient checking
输入:
def forward_propagation(x, theta):
"""
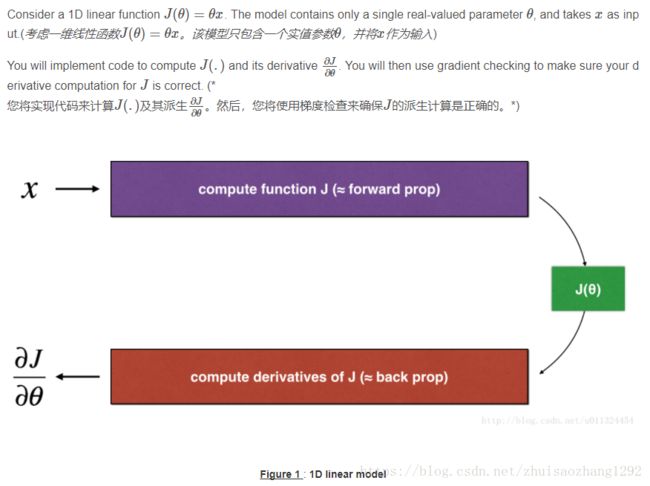
Implement the linear forward propagation (compute J) presented in Figure 1 (J(theta) = theta * x)
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
Returns:
J -- the value of function J, computed using the formula J(theta) = theta * x
"""
### START CODE HERE ### (approx. 1 line)
J = np.dot(theta,x)
### END CODE HERE ###
return J
def backward_propagation(x, theta):
"""
Computes the derivative of J with respect to theta (see Figure 1).
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
Returns:
dtheta -- the gradient of the cost with respect to theta
"""
### START CODE HERE ### (approx. 1 line)
dtheta = x
### END CODE HERE ###
return dtheta
def gradient_check(x, theta, epsilon = 1e-7):
"""
Implement the backward propagation presented in Figure 1.
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
Returns:
difference -- difference (2) between the approximated gradient and the backward propagation gradient
"""
# Compute gradapprox using left side of formula (1). epsilon is small enough, you don't need to worry about the limit.
### START CODE HERE ### (approx. 5 lines)
thetaplus = theta + epsilon # Step 1
thetaminus = theta - epsilon # Step 2
J_plus = forward_propagation(x, thetaplus) # Step 3
J_minus = forward_propagation(x, thetaminus) # Step 4
gradapprox = (J_plus - J_minus)/(2*epsilon) # Step 5
### END CODE HERE ###
# Check if gradapprox is close enough to the output of backward_propagation()
### START CODE HERE ### (approx. 1 line)
grad = backward_propagation(x, theta)
### END CODE HERE ###
### START CODE HERE ### (approx. 1 line)
numerator = np.linalg.norm(grad - gradapprox) # Step 1'
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox) # Step 2'
difference = numerator/denominator # Step 3'
### END CODE HERE ###
if difference < 1e-7:
print ("The gradient is correct!")
else:
print ("The gradient is wrong!")
return difference
x, theta = 2, 4
difference = gradient_check(x, theta)
print("difference = " + str(difference))输出:
The gradient is correct!
difference = 2.91933588329e-10
3) N-dimensional gradient checking
The following figure describes the forward and backward propagation of your fraud detection model.
Let’s look at your implementations for forward propagation and backward propagation
输入:
import numpy as np
from testCases import *
from gc_utils import sigmoid, relu, dictionary_to_vector, vector_to_dictionary, gradients_to_vector
def forward_propagation_n(X, Y, parameters):
"""
Implements the forward propagation (and computes the cost) presented in Figure 3.
Arguments:
X -- training set for m examples
Y -- labels for m examples
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
W1 -- weight matrix of shape (5, 4)
b1 -- bias vector of shape (5, 1)
W2 -- weight matrix of shape (3, 5)
b2 -- bias vector of shape (3, 1)
W3 -- weight matrix of shape (1, 3)
b3 -- bias vector of shape (1, 1)
Returns:
cost -- the cost function (logistic cost for one example)
"""
# retrieve parameters
m = X.shape[1]
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
# Cost
logprobs = np.multiply(-np.log(A3),Y) + np.multiply(-np.log(1 - A3), 1 - Y)
cost = 1./m * np.sum(logprobs)
cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3)
return cost, cache
def backward_propagation_n(X, Y, cache):
"""
Implement the backward propagation presented in figure 2.
Arguments:
X -- input datapoint, of shape (input size, 1)
Y -- true "label"
cache -- cache output from forward_propagation_n()
Returns:
gradients -- A dictionary with the gradients of the cost with respect to each parameter, activation and pre-activation variables.
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T) #不需要乘2 dW2 = 1./m * np.dot(dZ2, A1.T) * 2
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True) #前面4改为1 db1 = 4./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,
"dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2,
"dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
def gradient_check_n(parameters, gradients, X, Y, epsilon = 1e-7):
"""
Checks if backward_propagation_n computes correctly the gradient of the cost output by forward_propagation_n
Arguments:
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
grad -- output of backward_propagation_n, contains gradients of the cost with respect to the parameters.
x -- input datapoint, of shape (input size, 1)
y -- true "label"
epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
Returns:
difference -- difference (2) between the approximated gradient and the backward propagation gradient
"""
# Set-up variables
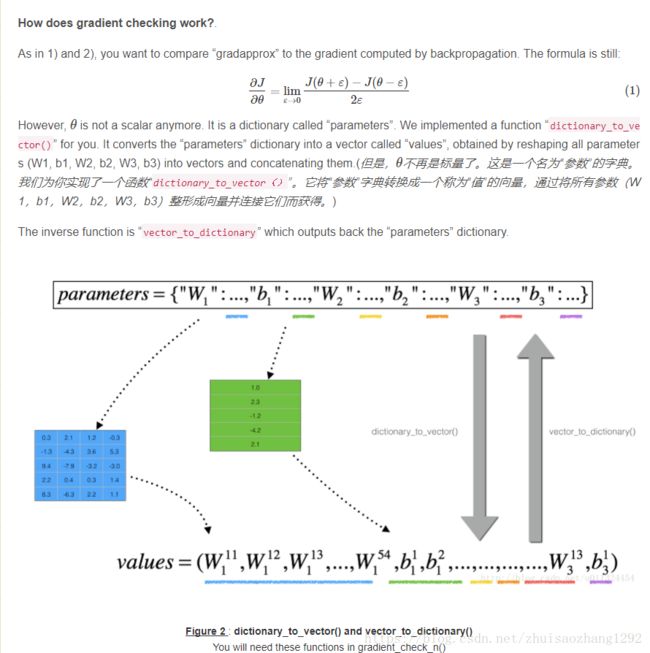
parameters_values, _ = dictionary_to_vector(parameters)
grad = gradients_to_vector(gradients)
num_parameters = parameters_values.shape[0]
J_plus = np.zeros((num_parameters, 1))
J_minus = np.zeros((num_parameters, 1))
gradapprox = np.zeros((num_parameters, 1))
# Compute gradapprox
for i in range(num_parameters):
# Compute J_plus[i]. Inputs: "parameters_values, epsilon". Output = "J_plus[i]".
# "_" is used because the function you have to outputs two parameters but we only care about the first one
### START CODE HERE ### (approx. 3 lines)
thetaplus = np.copy(parameters_values) # Step 1
thetaplus[i][0] = thetaplus[i][0] + epsilon # Step 2
J_plus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaplus)) # Step 3
### END CODE HERE ###
# Compute J_minus[i]. Inputs: "parameters_values, epsilon". Output = "J_minus[i]".
### START CODE HERE ### (approx. 3 lines)
thetaminus = np.copy(parameters_values) # Step 1
thetaminus[i][0] = thetaminus[i][0] - epsilon # Step 2
J_minus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaminus)) # Step 3
### END CODE HERE ###
# Compute gradapprox[i]
### START CODE HERE ### (approx. 1 line)
gradapprox[i] = (J_plus[i] - J_minus[i])/(2*epsilon)
### END CODE HERE ###
# Compare gradapprox to backward propagation gradients by computing difference.
### START CODE HERE ### (approx. 1 line)
numerator = np.linalg.norm(grad - gradapprox) # Step 1'
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox) # Step 2'
difference = numerator/denominator # Step 3'
### END CODE HERE ###
if difference > 1e-7:
print ( "There is a mistake in the backward propagation! difference = " + str(difference) )
else:
print ( "Your backward propagation works perfectly fine! difference = " + str(difference) )
return difference
X, Y, parameters = gradient_check_n_test_case()
cost, cache = forward_propagation_n(X, Y, parameters)
gradients = backward_propagation_n(X, Y, cache)
difference = gradient_check_n(parameters, gradients, X, Y)
Can you get gradient check to declare your derivative computation correct? Even though this part of the assignment isn’t graded, we strongly urge you to try to find the bug and re-run gradient check until you’re convinced backprop is now correctly implemented. (你能得到梯度检查来声明你的派生计算是正确的吗?即使这部分任务没有分级,但我们强烈建议您尝试查找错误并重新运行梯度检查,直到您确信backprop现在已正确实施。)
What you should remember from this notebook:
- Gradient checking verifies closeness between the gradients from backpropagation and the numerical approximation of the gradient (computed using forward propagation).
- Gradient checking is slow, so we don’t run it in every iteration of training. You would usually run it only to make sure your code is correct, then turn it off and use backprop for the actual learning process.
附录:
testCases.py
# -*- coding: utf-8 -*-
"""
Created on Sun Apr 22 12:57:30 2018
@author: StephenGai
"""
import numpy as np
def compute_cost_with_regularization_test_case():
np.random.seed(1)
Y_assess = np.array([[1, 1, 0, 1, 0]])
W1 = np.random.randn(2, 3)
b1 = np.random.randn(2, 1)
W2 = np.random.randn(3, 2)
b2 = np.random.randn(3, 1)
W3 = np.random.randn(1, 3)
b3 = np.random.randn(1, 1)
parameters = {"W1": W1, "b1": b1, "W2": W2, "b2": b2, "W3": W3, "b3": b3}
a3 = np.array([[ 0.40682402, 0.01629284, 0.16722898, 0.10118111, 0.40682402]])
return a3, Y_assess, parameters
def backward_propagation_with_regularization_test_case():
np.random.seed(1)
X_assess = np.random.randn(3, 5)
Y_assess = np.array([[1, 1, 0, 1, 0]])
cache = (np.array([[-1.52855314, 3.32524635, 2.13994541, 2.60700654, -0.75942115],
[-1.98043538, 4.1600994 , 0.79051021, 1.46493512, -0.45506242]]),
np.array([[ 0. , 3.32524635, 2.13994541, 2.60700654, 0. ],
[ 0. , 4.1600994 , 0.79051021, 1.46493512, 0. ]]),
np.array([[-1.09989127, -0.17242821, -0.87785842],
[ 0.04221375, 0.58281521, -1.10061918]]),
np.array([[ 1.14472371],
[ 0.90159072]]),
np.array([[ 0.53035547, 5.94892323, 2.31780174, 3.16005701, 0.53035547],
[-0.69166075, -3.47645987, -2.25194702, -2.65416996, -0.69166075],
[-0.39675353, -4.62285846, -2.61101729, -3.22874921, -0.39675353]]),
np.array([[ 0.53035547, 5.94892323, 2.31780174, 3.16005701, 0.53035547],
[ 0. , 0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. , 0. ]]),
np.array([[ 0.50249434, 0.90085595],
[-0.68372786, -0.12289023],
[-0.93576943, -0.26788808]]),
np.array([[ 0.53035547],
[-0.69166075],
[-0.39675353]]),
np.array([[-0.3771104 , -4.10060224, -1.60539468, -2.18416951, -0.3771104 ]]),
np.array([[ 0.40682402, 0.01629284, 0.16722898, 0.10118111, 0.40682402]]),
np.array([[-0.6871727 , -0.84520564, -0.67124613]]),
np.array([[-0.0126646]]))
return X_assess, Y_assess, cache
def forward_propagation_with_dropout_test_case():
np.random.seed(1)
X_assess = np.random.randn(3, 5)
W1 = np.random.randn(2, 3)
b1 = np.random.randn(2, 1)
W2 = np.random.randn(3, 2)
b2 = np.random.randn(3, 1)
W3 = np.random.randn(1, 3)
b3 = np.random.randn(1, 1)
parameters = {"W1": W1, "b1": b1, "W2": W2, "b2": b2, "W3": W3, "b3": b3}
return X_assess, parameters
def backward_propagation_with_dropout_test_case():
np.random.seed(1)
X_assess = np.random.randn(3, 5)
Y_assess = np.array([[1, 1, 0, 1, 0]])
cache = (np.array([[-1.52855314, 3.32524635, 2.13994541, 2.60700654, -0.75942115],
[-1.98043538, 4.1600994 , 0.79051021, 1.46493512, -0.45506242]]), np.array([[ True, False, True, True, True],
[ True, True, True, True, False]], dtype=bool), np.array([[ 0. , 0. , 4.27989081, 5.21401307, 0. ],
[ 0. , 8.32019881, 1.58102041, 2.92987024, 0. ]]), np.array([[-1.09989127, -0.17242821, -0.87785842],
[ 0.04221375, 0.58281521, -1.10061918]]), np.array([[ 1.14472371],
[ 0.90159072]]), np.array([[ 0.53035547, 8.02565606, 4.10524802, 5.78975856, 0.53035547],
[-0.69166075, -1.71413186, -3.81223329, -4.61667916, -0.69166075],
[-0.39675353, -2.62563561, -4.82528105, -6.0607449 , -0.39675353]]), np.array([[ True, False, True, False, True],
[False, True, False, True, True],
[False, False, True, False, False]], dtype=bool), np.array([[ 1.06071093, 0. , 8.21049603, 0. , 1.06071093],
[ 0. , 0. , 0. , 0. , 0. ],
[ 0. , 0. , 0. , 0. , 0. ]]), np.array([[ 0.50249434, 0.90085595],
[-0.68372786, -0.12289023],
[-0.93576943, -0.26788808]]), np.array([[ 0.53035547],
[-0.69166075],
[-0.39675353]]), np.array([[-0.7415562 , -0.0126646 , -5.65469333, -0.0126646 , -0.7415562 ]]), np.array([[ 0.32266394, 0.49683389, 0.00348883, 0.49683389, 0.32266394]]), np.array([[-0.6871727 , -0.84520564, -0.67124613]]), np.array([[-0.0126646]]))
return X_assess, Y_assess, cache
def gradient_check_n_test_case():
np.random.seed(1)
x = np.random.randn(4,3)
y = np.array([1, 1, 0])
W1 = np.random.randn(5,4)
b1 = np.random.randn(5,1)
W2 = np.random.randn(3,5)
b2 = np.random.randn(3,1)
W3 = np.random.randn(1,3)
b3 = np.random.randn(1,1)
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2,
"W3": W3,
"b3": b3}
return x, y, parameters
gc_utils.py
# -*- coding: utf-8 -*-
"""
Created on Sun Apr 22 18:21:39 2018
@author: StephenGai
"""
import numpy as np
def sigmoid(x):
"""
Compute the sigmoid of x
Arguments:
x -- A scalar or numpy array of any size.
Return:
s -- sigmoid(x)
"""
s = 1/(1+np.exp(-x))
return s
def relu(x):
"""
Compute the relu of x
Arguments:
x -- A scalar or numpy array of any size.
Return:
s -- relu(x)
"""
s = np.maximum(0,x)
return s
def dictionary_to_vector(parameters):
"""
Roll all our parameters dictionary into a single vector satisfying our specific required shape.
"""
keys = []
count = 0
for key in ["W1", "b1", "W2", "b2", "W3", "b3"]:
# flatten parameter
new_vector = np.reshape(parameters[key], (-1,1))
keys = keys + [key]*new_vector.shape[0]
if count == 0:
theta = new_vector
else:
theta = np.concatenate((theta, new_vector), axis=0)
count = count + 1
return theta, keys
def vector_to_dictionary(theta):
"""
Unroll all our parameters dictionary from a single vector satisfying our specific required shape.
"""
parameters = {}
parameters["W1"] = theta[:20].reshape((5,4))
parameters["b1"] = theta[20:25].reshape((5,1))
parameters["W2"] = theta[25:40].reshape((3,5))
parameters["b2"] = theta[40:43].reshape((3,1))
parameters["W3"] = theta[43:46].reshape((1,3))
parameters["b3"] = theta[46:47].reshape((1,1))
return parameters
def gradients_to_vector(gradients):
"""
Roll all our gradients dictionary into a single vector satisfying our specific required shape.
"""
count = 0
for key in ["dW1", "db1", "dW2", "db2", "dW3", "db3"]:
# flatten parameter
new_vector = np.reshape(gradients[key], (-1,1))
if count == 0:
theta = new_vector
else:
theta = np.concatenate((theta, new_vector), axis=0)
count = count + 1
return theta