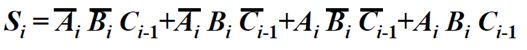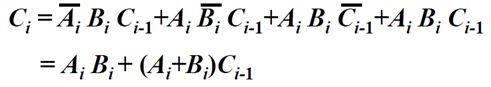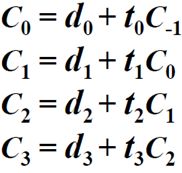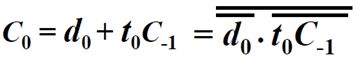数据面试小充电：数据的表示和运算

进制转换

◆ ◆ ◆ ◆

计算机中，二进制是最广泛的一种数制，以高低电平来表示二进制。当数码很大时，书写不方便，从而引进八进制和十六进制，但是其实计算机内部都是二进制。

我们熟悉的十进制如何在计算机中表示呢，比如把十进制数19.6875转化为二进制。

首先整数部分和小数部分需要分开来算。

整数部分：除2取余，自下而上

19/2=9  余1

9/2=4    余1

4/2=2    余0

2/2=1    余0

1/2=0    余1

（商为0为结束标志）

所以余数自下而上写：10011

小数部分：乘2取整，自上而下

0.6875*2=1.375 取1 余0.375

0.375*2=0.75     取0 余0.75

0.75*2=1.5         取1 余0.5

0.5*2=1              取1 余0

（取1余0为结束标志）

所以自上而下表示：1011

综上，19.6875的二进制表示为：10011.1011

真值和计算机数

◆ ◆ ◆ ◆

日常表示为+6、-8、-0.756这样的数成为真值。但是计算机并不知道“+”，“-”。由于0、1正好为两种状态，于是就规定0表示正号，1表示负号，这样被数字化的数就称为计算机数

BCD码

◆ ◆ ◆ ◆

二进制编码的十进制数（Binary Coded Decimal,BCD）是以二进制数来编码表示二进制0-9，分为两类：有权BCD码，如8421码、2421码、5421码等；无权BCD码，如余3码、格雷码等

（1）8421码：用四位二进制数表示一位十进制数，权值从高到低为8，4，2，1。如101001表示29

（2）余3码：8421码的基础上加上十进制3

定点数的表示

◆ ◆ ◆ ◆

1. 无符号数表示：整个机器字长全部二进制均为数值，没有符号为，相当于数的绝对值，如机器字长为8位，表示范围为0-2^8-1，即0-255

2. 有符号数表示：0表示正号，1表示负号，一般为：原码、补码、反码

   （1）3种机器数的最高位都为符号位

   （2）当真值为正数时，原码、补码、反码的表示均相同，即符号位为0，数值部分和真值相同

   （3）当真值为负数时，符号位为1，数值部分，补码是原码的“每位求反加1”，反码为原码的“每位求反”。注意：仅数值部分，不包括符号

   如：+1110，原，补，反均为01110

   -1101，原码：11101，补码：10011，反码：10010

3. 0的原码和反码都有两种，补码只有一种

表示范围如下：

原码：-（2^(n-1) -1）~ (2^(n-1) -1)

补码：-2^(n-1) ~ (2^(n-1) -1)

反码：-（2^(n-1) -1）~ (2^(n-1) -1)

移码

◆ ◆ ◆ ◆

介绍一下补码的缺点，举个例子

从代码形式上看，符号位也是一位二进制，将这些二进制代码进行比较，会得出101011>010101,100001>011111，其实恰好相反，这就是补码的缺点，但是可以通过移码来弥补。

将每一个真值加上2^n,如例子中n为5，得到

这样就能得到110101>001011,111111>000001

加上真值的过程其实就是移码

是不是比较懵逼……

其实，移码就是补码的符号位取反

补码的好处

◆ ◆ ◆ ◆

假设机器字长为4位，一位为符号，则补码的范围为-8~7，列出看一下

0000  0     1000  -8

0001  1     1001  -7

0010  2     1010  -6

0011  3     1011  -5

0100  4     1101  -4

0101  5     1101  -3

0110  6     1110  -2

0111  7     1111  -1

优点1：补码的设计可以满足x+(-x)=0，因为高位进位舍去；知道x的补码，求-x的补码，为：x的补码连同符号位在内每位取反再加1。

优点2：0的补码只有一种

优点3：补码的符号位可以参与运算，不需要单独设置电路

优点4：采用补码运算后，补码可以将正数加负数转化为正数加正数，又可以将减法转换为加法运算，这样就只设加法器就可以了

优点5：补码可以解决补码数的扩充问题。因为在补码表示中，全“1”代表-1，所以对负数补码进行扩充，可以直接补符号位，如1001扩充为8位，可以写为11111001；0111扩充为8位，可以写为：00000111

所以大部分计算机系统都采用补码来表示机器数

定点数的移位运算

◆ ◆ ◆ ◆

当某个二进制数相对于小数点做n位左移或者右移时，相当于该数乘以或者除以2的n次方。由于计算机中的机器字长都是固定的，当机器数左移或者右移时，都会使其n位低位或者n位高位出现空缺，就需要补0或者补1。需要考虑逻辑位移和算术位移。

（1）逻辑移位：逻辑左移时，高位移丢，低位补0；逻辑右移时，低位移丢，高位补0。如寄存器的内容为：10001010，逻辑左移为00010100，逻辑右移为01000101.

（2）算术移位：

<1>当机器数为正时，

1）原码：左移右移都补0

2）补码：左移右移都补0

3）反码：左移右移都补0

<2>当机器数为负时，

1）原码：左移右移都补0

2）补码：左移补0右移补1

3）反码：左移右移都补1

补码定点数的加/减法运算

◆ ◆ ◆ ◆

（1）补码加法：符号位参加运算，两数和的补码等于两数的补码之和，公式为

[x+y]补=[x]补+[y]补

（2）补码减法：运算器只包含加法器，于是需要用到[y]补和[-y]补，公式为

[x-y]补=[x]补+[-y]补

加减法的溢出判断

◆ ◆ ◆ ◆

（1）一位符号位判断溢出：一个正数和一个负数相加是不会溢出的。参加运算的两个数符号相同，其结果的符号可能与操作数不同，即为溢出，硬件实现判断为：

最高有效位的进位异或符号位的进位=1

则为溢出

比如：两个正数相加，符号位都是0，数值的最高位产生进位1，这个进位会进到符号位，符号位由0变成1且不会向上产生进位。所以最高有效位的进位=1，符号位进位=0，异或等于1，产生溢出。如果两个操作数都是负数，如果数值的最高位向上没有进位=0，因为符号位都是1，符号位向上进位=1，产生溢出。

（2）两位符号位溢出判断：双符号位相同，则未溢出，双符号位不同，则为溢出，最高符号位代表真正的符号。

补码乘法一位乘

◆ ◆ ◆ ◆

1. 被乘数与部分积一般取双符号位，并且符号位参与运算。（原因：一旦产生溢出，单符号位会出错，而双符号位的最高位是正确的符号位）

2. 乘数取单符号位以决定最后一步是否需要校正，即是否加[-x]补

3. 乘数末尾增设附件位Y（n+1),初始值为0

4. 根据Yn和Y（n+1）判断位，进行运算，步骤同上

5. 根据上述算法进行n+1步，但是第n+1步不再移位，仅根据Y0,Y1比较结果决定是否要加[x]补

6. 按补码移位规则，即部分积为正时，右移过程中有效位最高位补0；部分积为负时，右移过程中有效位最高位补1；双符号的移位中，次高符号位参与移位，最高位不参与

针对第四步，给出下列规则表

是不是很懵，用一个例子来看一下：

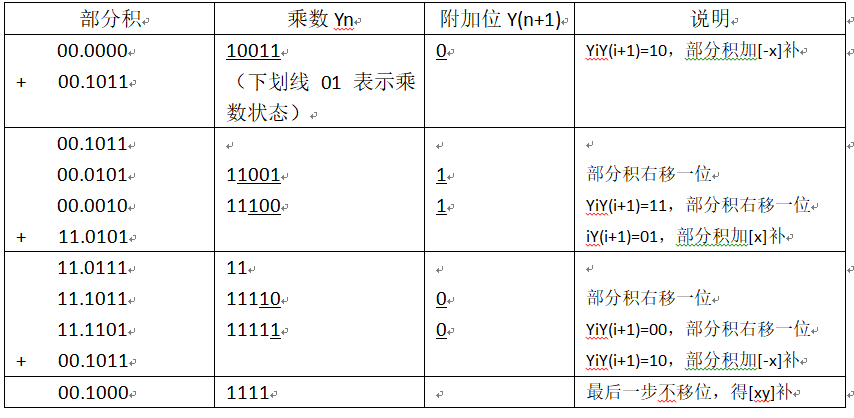
已知[x]补=1.0101，[y]补=1.0011，求[xy]补

解：先求[-x]补=0.1011,详细过程如下

看懂表格可能就了解得差不多了。如果看不懂，可以加小明同学聊聊。

算数逻辑单元ALU

◆ ◆ ◆ ◆

数字电路一般可分为组合逻辑电路和时序逻辑电路。

1. 组合逻辑电路：在逻辑功能上的特点是任意时刻的输出仅仅取决于该时刻的输入，与电路原来的状态无关。也就是说，组合逻辑电路没有记忆功能，运算后的结果要立刻送入寄存器保存

2. 时序逻辑电路：在逻辑功能上的特点是任意时刻的输出不仅取决于当时的输入信号，还取决于电路原来的状态。也就是说，时序逻辑电路具有记忆元件，即触发器（能够存储一位信号的基本单元电路），可以记录前一时刻的输出状态。

ALU是一种组合逻辑电路，因此实际使用ALU时，其输入端口A和B必须与锁存器相连，而且运算过程中锁存器（多位触发器）的内容是不变的，其输出必须送至寄存器保存。

ALU主要功能：ALU的功能不仅仅是执行算术（加、减、乘、除）和逻辑运算（与，或，非，异或）的部件，还具有先行进位逻辑。在并行加法器的并行进位链就是使用ALU。

下图就是ALU的电路框架

其中A，B为输入变量，K为控制信号，K的不同取值可以决定该电路进行哪一种算数运算或哪一种逻辑运算，F为输出

串行加法器

◆ ◆ ◆ ◆

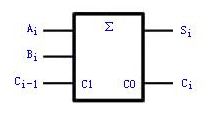
首先介绍一下全加器。全机器是一个加法单元，而一个加法单元是一个三端输入、两端输入的加法网络，如图所示

其中Ai代表被加数，Bi代表加数，Ci-1代表低位穿来的进位，Ci代表本位向高位的进位，和为Si

只设一个全加器的加法器称为串行加法器。两个操作数分别放到两个移位寄存器中，并且由移位寄存器从低位到高位串行地提供操作数进行相加。如果操作数长16位，就需要分成16步进行，每步产生一为和，串行地送入结果寄存器，而产生的进位信号只需要一位触发器，每完成一步，用新的进位覆盖旧的进位。串行加法器的结构如下图

所得的结果保存在操作数A的寄存器中，但是每次都是一位参与运算，速度太慢。如果操作数长16位，就需要分成16步进行，这是不可接受的。于是就有并行加法器

并行加法器

◆ ◆ ◆ ◆

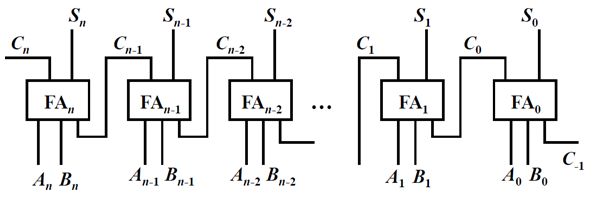
由n+1个全加器构成的并行加法器，这样两个n+1位的数可以利用这个加法器并行计算。

对于每一个全加器，有三个输入，其中两个输入对应了参与运算的两个数的响应位，另一个输入是低位的进位。有两个输出，一个输出是对应的加法和的结果对应位，另一个输出是本地产生的向高位的进位

每个全加器的结果Si是如何产生的呢？

Si指出了运算结果某一位到底是1还是0.如果输入的三位都是1或者其中一位是1，另外两个是0，对应的Si就为1，表达式为

这个表达式中，A和B都是参与运算的数据，保存在寄存器中，但是Ci-1是由低位产生的进位，只有这个进位产生后，才能计算出Si。所以影响速率就是Ci-1的产生。

那进位C是如何产生的呢？

如果三个输入都是1，或者两个输入是1，一个输入是0，就会产生进位，表示为

我们把AiBi叫做本地进位，也就是本地参与运算的两个数据响应的位就会产生的进位。另外Ai+Bi表示传送条件，用ti表示。如果这个或的值为1，那么Ci-1的结果就会被传送到Ci。所以我们就知道进位也可以由输入的Ai和Bi知道，所以就能快速产生进位了。

我们记AiBi为di，则进位表示如下

串行进位链

◆ ◆ ◆ ◆

进位链：传送进位的电路。也就是说在加法器中，我们可以把进位产生的电路独立出来，产生进位以后相应的进位再和AiBi一起参与运算生成Si。

我们以4位全加器为例，则每一位的进位表达式为

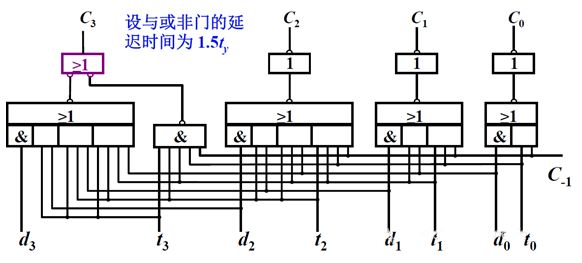
为了使用与非门实现进位链，对上面表达式进行变换，则

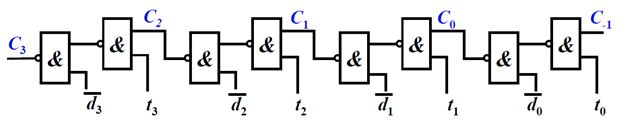
根据表达式，得出通过与非门产生的串行进位链：每个进位的产生需要采用两个与非门。如C0为例，根据变换的结果，使用t0和C-1的与操作，再做非操作输出，之后用d0的非和之前得到的结果再做与操作，非操作，就可以得到C0。这样我们就可以依次得到如下串行进位链。

并行进位链

◆ ◆ ◆ ◆

串行加法还是太慢了怎么办呢，这样就可以考虑是不是可以并行输出，让n位的加法器的进位同时产生。

首先对串行进位链中得到的表达式再进行变换得到如下

回顾一下，ti=AiBi,di=Ai+Bi

这样我们就可以由每一位参与运算的的位直接得出了所有进位了！这种称为并行进位或者跳跃进位。

单重分组跳跃进位链

◆ ◆ ◆ ◆

上图的跳跃进位的电路很复杂，而且才4位数。如果是32位或者64位，则会非常庞大而且复杂。为此又产生了两种折中的跳跃进位链。

n位全加器分成若干个小组，每个小组中的进位同时产生，小组之间串行进位。

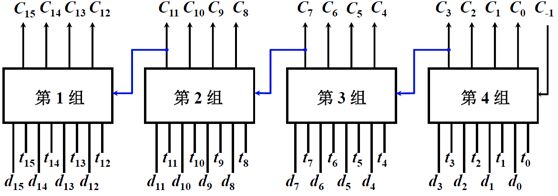
以16位为例子

上图中，组和组之间采用串行进位，也就是说当第四组中的C3产生以后，把C3作为输入输入到第三组中，这个C3和第三组中的di，ti配合，生成第三组中的所有Ci，同样第二组，第一组同理。

双重分组跳跃进位链

◆ ◆ ◆ ◆

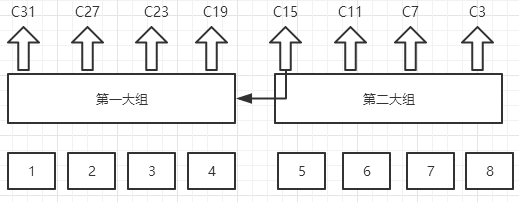
n 位全加器分若干大组，大组中又包含若干小组。每个大组中小组的最高位进位同时产生。大组与大组之间采用串行进位。

上图中，将32为分成2个大组，每个大组中分为四个小组，每个小组中四位。C3，C7，C11，C15对应了，8，7，6，5，四个小组的最高位的进位，这四个进位同时产生。同样，对第一大组来说C19，C23，C27，C31对应了4,3,2,1四个小组中的最高位进位，这四位进位也是同时产生。另外大组和大组之间采用串行进位的方式，也就是C15产生之后，作为输入，输入到第一大组中，用以产生第一大组中每个小组的最高位的进位和其他的进位。

查看往期精选：

月薪5万的java程序猿必备

抛砖引玉NIO

Java改善性能小技巧

深入理解final

String三姐妹你所不知道的坑！

面试必备SpringMVC工作原理，涨薪5K就靠它！

连阿里HR都知道的四种引用类型，你知道多少！

 升职加薪，点击关注，不要走丢~

无