tensorflow 2.0 深度学习(第二部分 part2)
日萌社
人工智能AI:Keras PyTorch MXNet TensorFlow PaddlePaddle 深度学习实战(不定时更新)
tensorflow 2.0 深度学习(第一部分 part1)
tensorflow 2.0 深度学习(第一部分 part2)
tensorflow 2.0 深度学习(第一部分 part3)
tensorflow 2.0 深度学习(第二部分 part1)
tensorflow 2.0 深度学习(第二部分 part2)
tensorflow 2.0 深度学习(第二部分 part3)
tensorflow 2.0 深度学习 (第三部分 卷积神经网络 part1)
tensorflow 2.0 深度学习 (第三部分 卷积神经网络 part2)
tensorflow 2.0 深度学习(第四部分 循环神经网络)
tensorflow 2.0 深度学习(第五部分 GAN生成神经网络 part1)
tensorflow 2.0 深度学习(第五部分 GAN生成神经网络 part2)
tensorflow 2.0 深度学习(第六部分 强化学习)
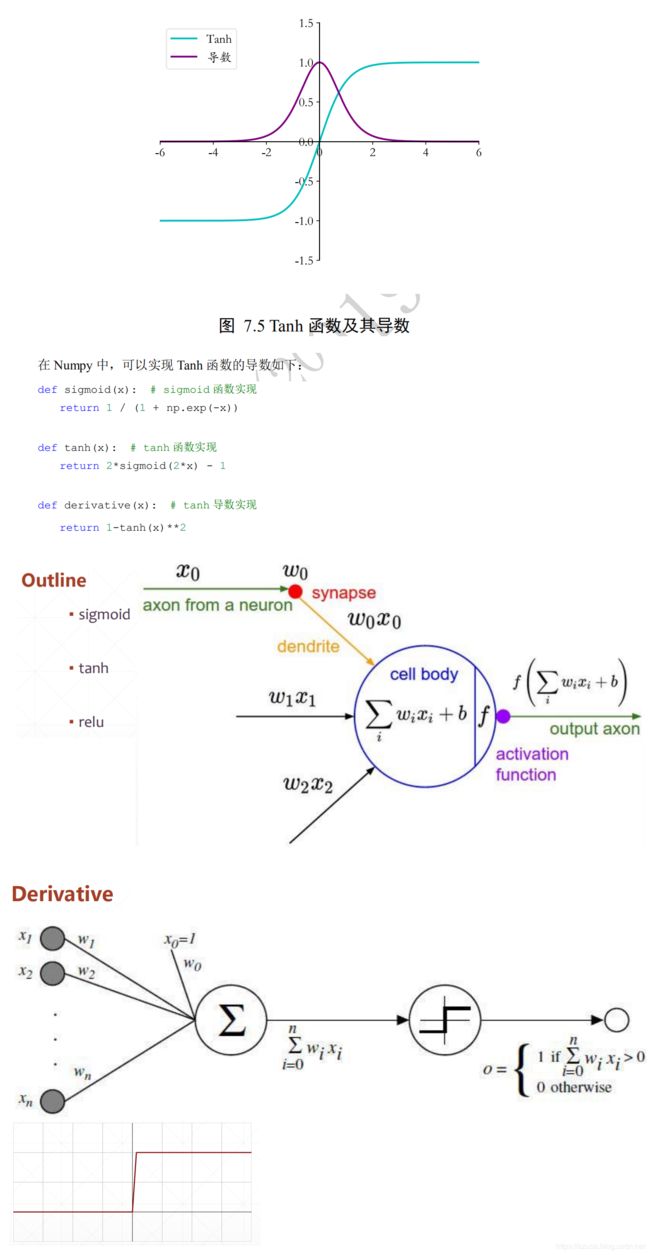
反向传播算法
导数与梯度
import tensorflow as tf
w = tf.Variable(1.0) #
b = tf.Variable(2.0) #
x = tf.Variable(3.0) #
#1.求导,tape.gradient(y,[参数θ])求参数θ相对于y的梯度信息
# dy_dw = tape.gradient(y, [w])
#2.通过tape.gradient(loss,[参数θ])函数求得网络参数θ的梯度信息
# grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# 根据loss对模型所有参数求导 tape.gradient(loss, model.trainable_variables)
with tf.GradientTape() as t1:
with tf.GradientTape() as t2:
y = x * w + b
dy_dw, dy_db = t2.gradient(y, [w, b])
d2y_dw2 = t1.gradient(dy_dw, w)
print(y) #tf.Tensor(5.0, shape=(), dtype=float32)
print(dy_dw) #tf.Tensor(3.0, shape=(), dtype=float32)
print(dy_db) #tf.Tensor(1.0, shape=(), dtype=float32)
print(d2y_dw2) #None
assert dy_dw.numpy() == 3.0 #dy_dw.numpy()值为3.0
assert d2y_dw2 is None
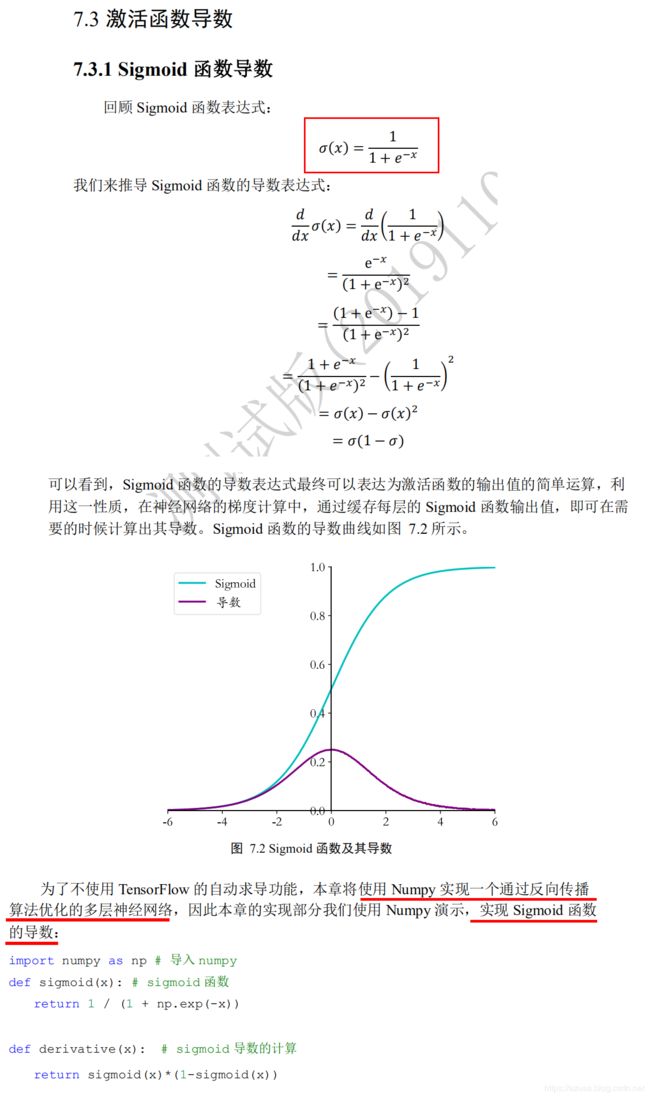
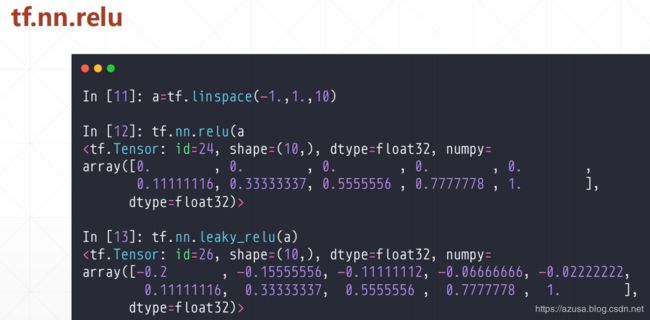
激活函数的导数
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import datasets, layers
def sigmoid(x): # sigmoid函数,也可以直接使用tf.nn.sigmoid
return 1 / (1 + tf.math.exp(-x))
def derivative(x): # sigmoid导数的计算
return sigmoid(x)*(1-sigmoid(x))
损失函数的梯度
全连接层的梯度
单输出感知机及其梯度
多输出感知机及其梯度
多层感知机及其梯度
链式法则
import tensorflow as tf
# 构建待优化变量
x = tf.constant(1.)
w1 = tf.constant(2.)
b1 = tf.constant(1.)
w2 = tf.constant(2.)
b2 = tf.constant(1.)
with tf.GradientTape(persistent=True) as tape:
# 非tf.Variable类型的张量需要人为设置记录梯度信息
tape.watch([w1, b1, w2, b2])
# 构建2层网络,前向计算
y1 = x * w1 + b1
y2 = y1 * w2 + b2
#1.求导,tape.gradient(y,[参数θ])求参数θ相对于y的梯度信息
# dy_dw = tape.gradient(y, [w])
#2.通过tape.gradient(loss,[参数θ])函数求得网络参数θ的梯度信息
# grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# 根据loss对模型所有参数求导 tape.gradient(loss, model.trainable_variables)
# 独立求解出各个导数
dy2_dy1 = tape.gradient(y2, [y1])[0]
dy1_dw1 = tape.gradient(y1, [w1])[0]
dy2_dw1 = tape.gradient(y2, [w1])[0]
# 验证链式法则:dy2_dy1 * dy1_dw1 == dy2_dw1
print(dy2_dy1 * dy1_dw1)
print(dy2_dw1)
import tensorflow as tf
x = tf.constant(1.)
w1 = tf.constant(2.)
b1 = tf.constant(1.)
w2 = tf.constant(2.)
b2 = tf.constant(1.)
with tf.GradientTape(persistent=True) as tape:
tape.watch([w1, b1, w2, b2])
y1 = x * w1 + b1
y2 = y1 * w2 + b2
#1.求导,tape.gradient(y,[参数θ])求参数θ相对于y的梯度信息
# dy_dw = tape.gradient(y, [w])
#2.通过tape.gradient(loss,[参数θ])函数求得网络参数θ的梯度信息
# grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# 根据loss对模型所有参数求导 tape.gradient(loss, model.trainable_variables)
# 独立求解出各个导数
dy2_dy1 = tape.gradient(y2, [y1])[0]
dy1_dw1 = tape.gradient(y1, [w1])[0]
dy2_dw1 = tape.gradient(y2, [w1])[0] #链式法则:dy2/dy1 * dy1/dw1 == dy2/dw1
print(dy2_dy1 * dy1_dw1)#验证链式法则:dy2_dy1 * dy1_dw1 == dy2_dw1
print(dy2_dw1)
import tensorflow as tf
x=tf.random.normal([1,3])
w=tf.ones([3,1])
b=tf.ones([1])
y = tf.constant([1])
with tf.GradientTape() as tape:
tape.watch([w, b])
logits = tf.sigmoid(x@w+b) #非线性激活函数sigmoid(线性函数x@w+b)
loss = tf.reduce_mean(tf.losses.MSE(y, logits)) #MSE均方差损失函数(真实值y - 预测值logits)
#1.求导,tape.gradient(y,[参数θ])求参数θ相对于y的梯度信息
# dy_dw = tape.gradient(y, [w])
#2.通过tape.gradient(loss,[参数θ])函数求得网络参数θ的梯度信息
# grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# 根据loss对模型所有参数求导 tape.gradient(loss, model.trainable_variables)
grads = tape.gradient(loss, [w, b])
print('w grad:', grads[0]) #w的梯度值
#tf.Tensor(
#[[ 0.03690954]
# [ 0.14418897]
# [-0.0085043 ]], shape=(3, 1), dtype=float32)
print('b grad:', grads[1]) #b的梯度值
#tf.Tensor([-0.22039364], shape=(1,), dtype=float32)
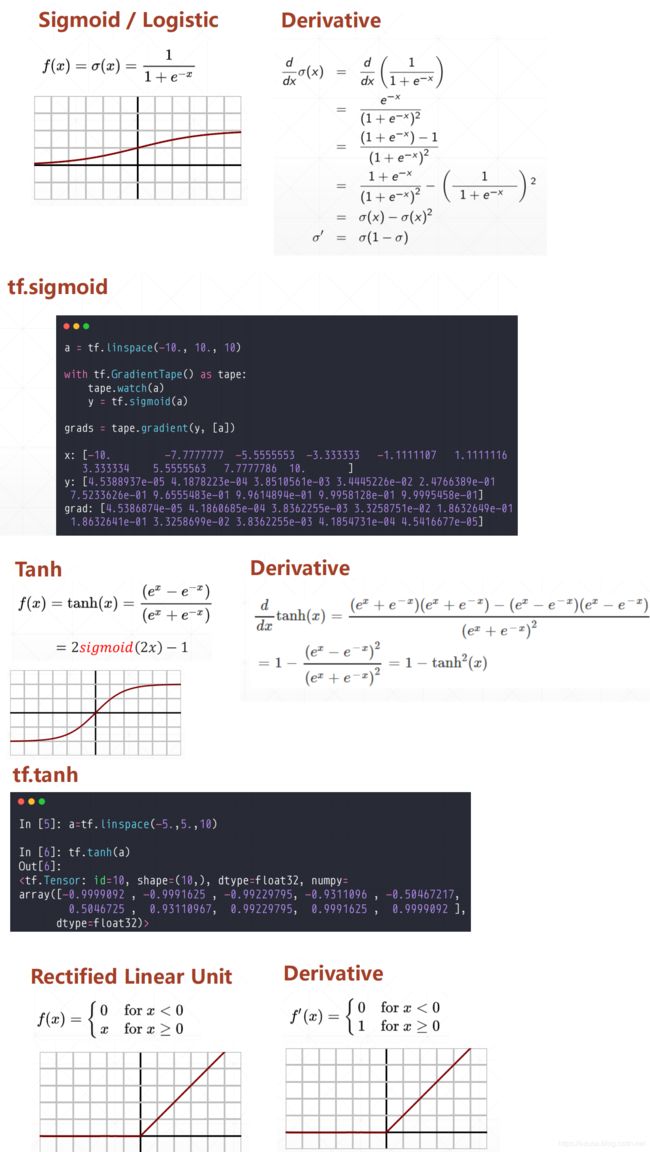
import tensorflow as tf
a = tf.linspace(-10., 10., 10)
with tf.GradientTape() as tape:
tape.watch(a)
y = tf.sigmoid(a)
grads = tape.gradient(y, [a])
print('x:', a.numpy())
#x: [-10. -7.7777777 -5.5555553 -3.333333 -1.1111107
# 1.1111116 3.333334 5.5555563 7.7777786 10. ]
print('y:', y.numpy())
#y: [4.5388937e-05 4.1878223e-04 3.8510561e-03 3.4445226e-02 2.4766389e-01
# 7.5233626e-01 9.6555483e-01 9.9614894e-01 9.9958128e-01 9.9995458e-01]
print('grad:', grads[0].numpy())
#grad: [4.5386874e-05 4.1860685e-04 3.8362255e-03 3.3258751e-02 1.8632649e-01
# 1.8632641e-01 3.3258699e-02 3.8362255e-03 4.1854731e-04 4.5416677e-05]
反向传播算法
Himmelblau 函数优化实战
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import pyplot as plt
import tensorflow as tf
def himmelblau(x):
# himmelblau 函数实现
return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2
#通过 np.meshgrid 函数(TensorFlow 中也有 meshgrid 函数)生成二维平面网格点坐标
x = np.arange(-6, 6, 0.1)
y = np.arange(-6, 6, 0.1)
#x,y range: (120,) (120,)
print('x,y range:', x.shape, y.shape)
# 生成 x-y 平面采样网格点,方便可视化。生成网格点,并拆分后返回所有点的 x,y 坐标张量。
# tf.meshgrid 会返回在 axis=2 维度切割后的 2 个张量 a,b,其中张量 a 包含了所有点的 x坐标,
# b 包含了所有点的 y 坐标,shape 都为[120,120]
X, Y = np.meshgrid(x, y)
#X,Y maps: (120, 120) (120, 120)
print('X,Y maps:', X.shape, Y.shape)
# 计算网格点上的函数值
# Z.shape (120, 120)
Z = himmelblau([X, Y])
# 利用 Matplotlib 库可视化 Himmelblau 函数
# 绘制 himmelblau 函数曲面
fig = plt.figure('himmelblau')
ax = fig.gca(projection='3d')
ax.plot_surface(X, Y, Z)
ax.view_init(60, -30)
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
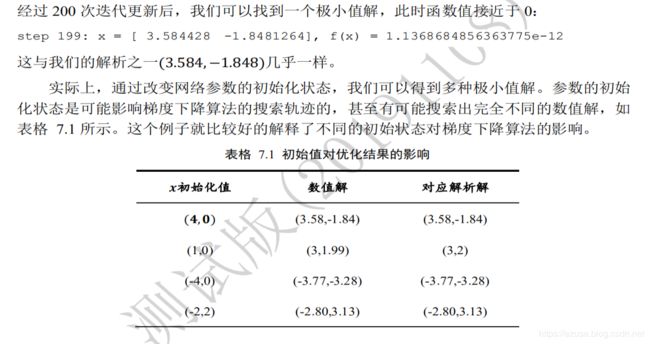
#1.参数的初始化值对优化的影响不容忽视,可以通过尝试不同的初始化值,检验函数优化的极小值情况
#2.初始化[X,Y]为tf.constant([-1., 0.])时,优化的Himmelblau函数[X,Y]为[-2.805118 3.1313126], 极小值Z为 f(x) = 2.273736618907049e-13,即0.0000000000002273736618907049
# 初始化[X,Y]为tf.constant([1., 0.])时,优化的Himmelblau函数[X,Y]为[3.0000002 1.9999996], 极小值Z为 f(x) = 1.818989620386291e-12,即0.000000000001818989620386291
# 初始化[X,Y]为tf.constant([-4., 0.])时,优化的Himmelblau函数[X,Y]为[-3.7793102 -3.283186 ], 极小值Z为 f(x) = 0.0
# 初始化[X,Y]为tf.constant([4., 0.])时,优化的Himmelblau函数[X,Y]为[ 3.584428 -1.8481264], 极小值Z为 f(x) = 1.1368684856363775e-12,即0.0000000000011368684856363775
#3.通过改变网络参数的初始化状态tf.constant([X,Y]),我们可以得到Himmelblau函数多种极小值解Z。大致可以从图上看出它共有 4个局部极小值点,
# 并且等高线上的局部极小值Z都是 0,所以这 4个局部极小值也是全局最小值。我们可以通过解析的方法计算出局部极小值Z的坐标X、Y,
# 他们分别是(3,2), (−2 805, 3 131), (−3 779, −3 283), (3 584, −1 848)。
# 参数的初始化状态tf.constant([X,Y])是可能影响梯度下降算法的搜索轨迹的,甚至有可能搜索出完全不同的数值解。
# 这个例子就比较好的解释了不同的初始状态对梯度下降算法的影响。
#4.下面的tf.constant([X,Y])初始化参数
x = tf.constant([4., 0.])
for step in range(200): # 循环优化 200 次
with tf.GradientTape() as tape: #梯度跟踪
tape.watch([x]) # 加入梯度跟踪列表
y = himmelblau(x) # 前向传播
# 反向传播
grads = tape.gradient(y, [x])[0]
# 更新参数,0.01 为学习率
x -= 0.01*grads
# 打印优化的极小值
if step % 20 == 19:
print ('step {}: x = {}, f(x) = {}'.format(step, x.numpy(), y.numpy()))
#step 19: x = [ 3.5381215 -1.3465767], f(x) = 3.7151756286621094
#step 39: x = [ 3.5843277 -1.8470242], f(x) = 3.451140582910739e-05
#step 59: x = [ 3.584428 -1.8481253], f(x) = 4.547473508864641e-11
#step 79: x = [ 3.584428 -1.8481264], f(x) = 1.1368684856363775e-12
#step 99: x = [ 3.584428 -1.8481264], f(x) = 1.1368684856363775e-12
#step 119: x = [ 3.584428 -1.8481264], f(x) = 1.1368684856363775e-12
#step 139: x = [ 3.584428 -1.8481264], f(x) = 1.1368684856363775e-12
#step 159: x = [ 3.584428 -1.8481264], f(x) = 1.1368684856363775e-12
#step 179: x = [ 3.584428 -1.8481264], f(x) = 1.1368684856363775e-12
#step 199: x = [ 3.584428 -1.8481264], f(x) = 1.1368684856363775e-12
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import pyplot as plt
import tensorflow as tf
def himmelblau(x):
return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2
x = np.arange(-6, 6, 0.1)
y = np.arange(-6, 6, 0.1)
print('x,y range:', x.shape, y.shape)
X, Y = np.meshgrid(x, y)
print('X,Y maps:', X.shape, Y.shape)
Z = himmelblau([X, Y])
fig = plt.figure('himmelblau')
ax = fig.gca(projection='3d')
ax.plot_surface(X, Y, Z)
ax.view_init(60, -30)
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
# [-1., 0.],[1., 0.], [-4, 0.], [4, 0.]
x = tf.constant([4., 0.])
for step in range(200):
with tf.GradientTape() as tape:
tape.watch([x])
y = himmelblau(x)
grads = tape.gradient(y, [x])[0]
x -= 0.01*grads
if step % 20 == 0:
print ('step {}: x = {}, f(x) = {}'.format(step, x.numpy(), y.numpy()))
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import pyplot as plt
import tensorflow as tf
def himmelblau(x):
# himmelblau函数实现
return (x[0] ** 2 + x[1] - 11) ** 2 + (x[0] + x[1] ** 2 - 7) ** 2
x = np.arange(-6, 6, 0.1)
y = np.arange(-6, 6, 0.1)
print('x,y range:', x.shape, y.shape)
# 生成x-y平面采样网格点,方便可视化
X, Y = np.meshgrid(x, y)
print('X,Y maps:', X.shape, Y.shape)
Z = himmelblau([X, Y]) # 计算网格点上的函数值
# 绘制himmelblau函数曲面
fig = plt.figure('himmelblau')
ax = fig.gca(projection='3d')
ax.plot_surface(X, Y, Z)
ax.view_init(60, -30)
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
# 参数的初始化值对优化的影响不容忽视,可以通过尝试不同的初始化值,
# 检验函数优化的极小值情况
# [-1., 0.], [1., 0.], [-4, 0.], [4, 0.]
# x = tf.constant([-1., 0.])
# x = tf.constant([4., 0.])
# x = tf.constant([1., 0.])
# x = tf.constant([-4., 0.])
x = tf.constant([-2., 2.])
for step in range(200):# 循环优化
with tf.GradientTape() as tape: #梯度跟踪
tape.watch([x]) # 记录梯度
y = himmelblau(x) # 前向传播
# 反向传播
grads = tape.gradient(y, [x])[0]
# 更新参数,0.01为学习率
x -= 0.01*grads
# 打印优化的极小值
if step % 20 == 19:
print ('step {}: x = {}, f(x) = {}'
.format(step, x.numpy(), y.numpy()))
反向传播算法实战
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
import seaborn as sns
from matplotlib import pyplot as plt
N_SAMPLES = 2000 # 采样点数
TEST_SIZE = 0.3 # 测试数量比率
# 利用工具函数直接生成数据集
X, y = make_moons(n_samples=N_SAMPLES, noise=0.2, random_state=100)
# 将 2000 个点按着 7:3 分割为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=TEST_SIZE, random_state=42)
print(X.shape, y.shape) # (2000, 2) (2000,)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape) # (1400, 2) (600, 2) (1400,) (600,)
# 绘制数据集的分布,X 为 2D 坐标,y 为数据点的标签
def make_plot(X, y, plot_name, file_name=None, XX=None, YY=None, preds=None, dark=False):
if (dark):
plt.style.use('dark_background')
else:
sns.set_style("whitegrid")
plt.figure(figsize=(16, 12))
axes = plt.gca()
axes.set(xlabel="$x_1$", ylabel="$x_2$")
plt.title(plot_name, fontsize=30)
plt.subplots_adjust(left=0.20)
plt.subplots_adjust(right=0.80)
if (XX is not None and YY is not None and preds is not None):
plt.contourf(XX, YY, preds.reshape(XX.shape), 25, alpha=1, cmap=cm.Spectral)
plt.contour(XX, YY, preds.reshape(XX.shape), levels=[.5], cmap="Greys", vmin=0, vmax=.6)
# 绘制散点图,根据标签区分颜色
plt.scatter(X[:, 0], X[:, 1], c=y.ravel(), s=40, cmap=plt.cm.Spectral, edgecolors='none')
plt.savefig('dataset.svg')
plt.close()
# 调用 make_plot 函数绘制数据的分布,其中 X 为 2D 坐标,y 为标签
make_plot(X, y, "Classification Dataset Visualization ")
plt.show()
import numpy as np
class Layer:
# 全连接网络层
def __init__(self, n_input, n_neurons, activation=None, weights=None, bias=None):
"""
:param int n_input: 输入节点数
:param int n_neurons: 输出节点数
:param str activation: 激活函数类型
:param weights: 权值张量,默认类内部生成
:param bias: 偏置,默认类内部生成
"""
# 通过正态分布初始化网络权值,初始化非常重要,不合适的初始化将导致网络不收敛
# weights [输入节点数,输出节点],bias [输出节点,]
self.weights = weights if weights is not None else np.random.randn(n_input, n_neurons) * np.sqrt(1 / n_neurons)
self.bias = bias if bias is not None else np.random.rand(n_neurons) * 0.1
self.activation = activation # 激活函数类型,如’sigmoid’
self.last_activation = None # 激活函数的输出值 o
self.error = None # 用于计算当前层的 delta 变量的中间变量
self.delta = None # 记录当前层的 delta 变量,用于计算梯度
# 网络层的前向传播
def activate(self, x):
# 前向传播
r = np.dot(x, self.weights) + self.bias # X@W+b
# 通过激活函数,得到全连接层的输出 o
self.last_activation = self._apply_activation(r)
return self.last_activation
# self._apply_activation 实现了不同的激活函数的前向计算过程
def _apply_activation(self, r):
# 计算激活函数的输出
if self.activation is None:
return r # 无激活函数,直接返回
# ReLU 激活函数
elif self.activation == 'relu':
return np.maximum(r, 0)
# tanh
elif self.activation == 'tanh':
return np.tanh(r)
# sigmoid
elif self.activation == 'sigmoid':
return 1 / (1 + np.exp(-r))
return r
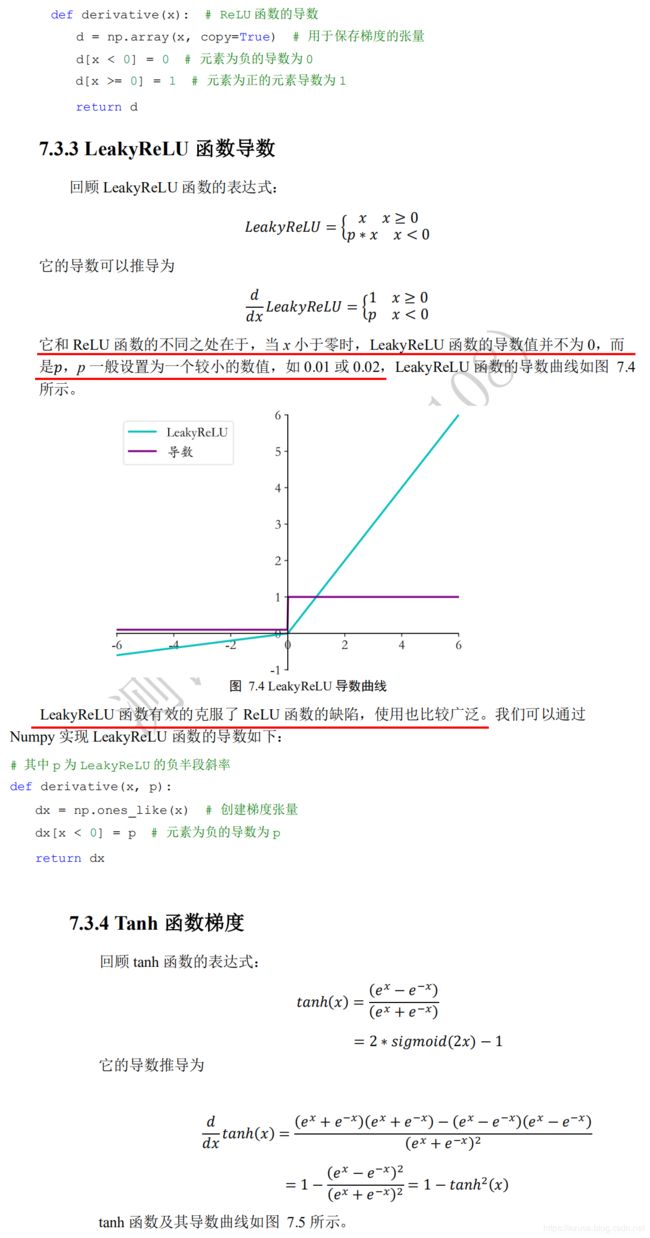
# 针对于不同的激活函数,它们的导数计算实现如下
def apply_activation_derivative(self, r):
# 计算激活函数的导数
# 无激活函数,导数为 1
if self.activation is None:
return np.ones_like(r)
# ReLU 函数的导数实现
elif self.activation == 'relu':
grad = np.array(r, copy=True)
grad[r > 0] = 1.
grad[r <= 0] = 0.
return grad
# tanh 函数的导数实现
elif self.activation == 'tanh':
return 1 - r ** 2
# Sigmoid 函数的导数实现
elif self.activation == 'sigmoid':
# 可以看到,Sigmoid 函数的导数实现为 ∗ (1 − ),其中即为()。
return r * (1 - r)
return r
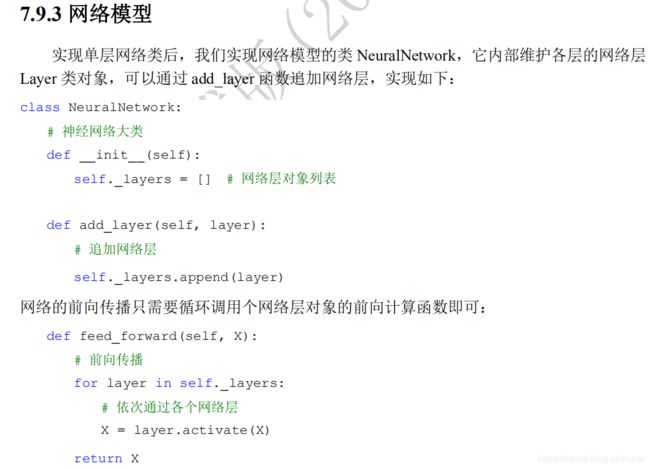
class NeuralNetwork:
# 神经网络大类
def __init__(self):
self._layers = [] # 网络层对象列表
def add_layer(self, layer):
# 追加网络层
self._layers.append(layer)
# 网络的前向传播只需要循环调用网络层对象的前向计算函数即可
def feed_forward(self, X):
# 前向传播
for layer in self._layers:
# 依次通过各个网络层
X = layer.activate(X)
return X
1.前向传播:
从前往后(从第一层隐藏层最后到输出层)
每一层中的第一步是线性函数w@x+b=z,每一层中的第二步是非线性函数(激活函数)。
最后输出层第二步激活函数的输出值作为预测值,输入到损失函数计算loss。
2.反向传播:
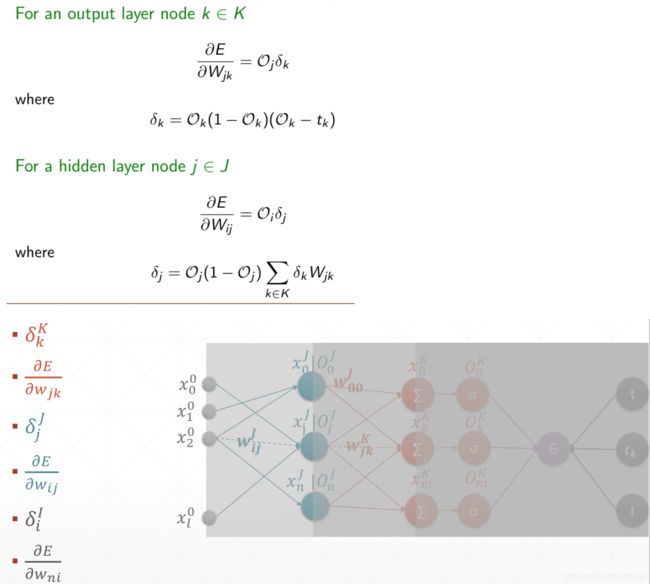
1.从后往前(输出层到第一层隐藏层)求每一层的delta变量
1.输出层:
= output(1 − output)(output − y) = (1 − )(y - output)
1.第一步:先计算损失函数的导数,比如此处计算均方差的导数:中间值error = 真实标签y - 预测值output,公式L/ = ( −yi),为output,yi为y。
2.第二步:然后计算激活函数的导数,比如此处计算Sigmoid的导数:output(1 − output),output为预测值,公式/ * () = (1 − )。
3.第三步:最后把损失函数导数值和激活函数导数值两者相乘得出delta变量值 = output(1 − output)(output − y) = (1 − )(y - output)。
2.最后一层隐藏层逐一计算到第一层隐藏层:
= activation(1 − activation) ∑j Jj ij
1.第一步:先计算当前层(比如第三层隐藏层)的下一层(比如输出层)的weights权重矩阵和delta变量值两者的dot矩阵相乘,
作为当前层的中间值error = np.dot(下一层weights, 下一层delta) = ∑j Jj ij,ij为下一层weights,下一层delta为Jj。
2.第二步:计算当前层激活函数的导数,比如此处计算Sigmoid的导数:activation(1 − activation),activation为激活函数输出值,公式/ * () = (1 − )。
3.第三步:最后把当前层的中间值error和激活函数导数值两者相乘得出delta变量值 = activation(1 − activation) ∑j Jj ij。
2.从前往后(第一层隐藏层到输出层)更新每一层的模型参数θ
L/θ = θ_grad = * 激活函数的输出o.T(或者输入层的输出o.T)
θ = θ - lr * θ_grad = θ - lr * L/θ
1.第一步:获取上一层网络层激活函数的输出o
1.第一层隐藏层:使用输入层的输出作为o。
2.第二层隐藏层到输出层:使用上一层网络层激活函数的输出activation作为o,比如第二层隐藏层使用第一层激活函数的输出activation作为o。
2.第二步:当前层delta变量值 * 激活函数的输出o.T(或者输入层的输出o.T) = θ_grad = L/θ
3.第三步:θ = θ - lr * θ_grad = θ - lr * L/θ:其中 L/θ表示loss对于参数θ的梯度表示为θ_grad,用于更新参数θ,lr为学习率。
class NeuralNetwork:
# 神经网络大类
def __init__(self):
self._layers = [] # 网络层对象列表
def add_layer(self, layer):
# 追加网络层
self._layers.append(layer)
# 网络的前向传播只需要循环调用网络层对象的前向计算函数即可
def feed_forward(self, X):
# 前向传播
for layer in self._layers:
# 依次通过各个网络层
X = layer.activate(X)
return X
"""
1.前向传播:
从前往后(从第一层隐藏层最后到输出层)
每一层中的第一步是线性函数w@x+b=z,每一层中的第二步是非线性函数(激活函数)。
最后输出层第二步激活函数的输出值作为预测值,输入到损失函数计算loss。
2.反向传播:
1.从后往前(输出层到第一层隐藏层)求每一层的delta变量
1.输出层:
= output(1 − output)(output − y) = (1 − )(y - output)
1.第一步:先计算损失函数的导数,比如此处计算均方差的导数:中间值error = 真实标签y - 预测值output,公式L/ = ( −yi),为output,yi为y。
2.第二步:然后计算激活函数的导数,比如此处计算Sigmoid的导数:output(1 − output),output为预测值,公式/ * () = (1 − )。
3.第三步:最后把损失函数导数值和激活函数导数值两者相乘得出delta变量值 = output(1 − output)(output − y) = (1 − )(y - output)。
2.最后一层隐藏层逐一计算到第一层隐藏层:
= activation(1 − activation) ∑j Jj ij
1.第一步:先计算当前层(比如第三层隐藏层)的下一层(比如输出层)的weights权重矩阵和delta变量值两者的dot矩阵相乘,
作为当前层的中间值error = np.dot(下一层weights, 下一层delta) = ∑j Jj ij,ij为下一层weights,下一层delta为Jj。
2.第二步:计算当前层激活函数的导数,比如此处计算Sigmoid的导数:activation(1 − activation),activation为激活函数输出值,
公式/ * () = (1 − )。
3.第三步:最后把当前层的中间值error和激活函数导数值两者相乘得出delta变量值 = activation(1 − activation) ∑j Jj ij。
2.从前往后(第一层隐藏层到输出层)更新每一层的模型参数θ
L/θ = θ_grad = * 激活函数的输出o.T(或者输入层的输出o.T)
θ = θ - lr * θ_grad = θ - lr * L/θ
1.第一步:获取上一层网络层激活函数的输出o
1.第一层隐藏层:使用输入层的输出作为o。
2.第二层隐藏层到输出层:使用上一层网络层激活函数的输出activation作为o,比如第二层隐藏层使用第一层激活函数的输出activation作为o。
2.第二步:当前层delta变量值 * 激活函数的输出o.T(或者输入层的输出o.T) = θ_grad = L/θ
3.第三步:θ = θ - lr * θ_grad = θ - lr * L/θ:其中 L/θ表示loss对于参数θ的梯度表示为θ_grad,用于更新参数θ,lr为学习率。
"""
# 网络模型的反向传播实现稍复杂,需要从最末层开始,计算每层的变量。
# 根据我们推导的梯度公式,将计算出的变量存储在 Layer 类的 delta 变量中,用于计算梯度。
# 在 backpropagation 函数中,反向计算每层的变量,并根据梯度公式计算每层参数的梯度值,按着梯度下降算法完成一次参数的更新。
def backpropagation(self, X, y, learning_rate):
# 反向传播算法实现
# 前向计算,得到输出值
output = self.feed_forward(X)
# range(4)+reversed表示 反转从大到小遍历为 3/2/1/0,即从最后一层输出层开始从后往前遍历每一层
for i in reversed(range(len(self._layers))): # 反向循环
layer = self._layers[i] # 得到当前层对象
# 如果是输出层,获取的是layers[3]==layers[-1]
if layer == self._layers[-1]: # 对于输出层
# 计算 2分类任务的均方差的导数 L/ = ( −yi)。y为yi,即真实值;output为 ,即模型输出层的sigmoid激活函数输出的预测值
# 第一步:计算损失函数的导数,此处为使用 均方差函数的导数 计算出当前层 delta变量的 中间变量error
# = (1 − )( − ),为输出层输出的预测值,为真实值,( − )即为 y - output
layer.error = y - output
# 关键步骤:计算最后一层的 delta,参考输出层的梯度公式,此处即计算输出层所使用的sigmoid的的导数
# 第二步:apply_activation_derivative计算激活函数的导数,此处为计算sigmoid激活函数的导数,output为 模型输出层的sigmoid激活函数输出的预测值,
# 中间变量error为均方差函数的导数值,将计算出的变量存储在Layer类的delta变量中,用于计算梯度。
# = (1 − )( − ),为输出层输出的预测值,为真实值,′ = (1 − ),将()写回形式,
# 即变成′ = (1 − ),(1 − )即为 apply_activation_derivative(output)
layer.delta = layer.error * layer.apply_activation_derivative(output)
# 如果是隐藏层,获取的分别为layers[2](第三层隐藏层)、layers[1](第二层隐藏层)、layers[0](第一层隐藏层)
else:
# 第一步:获取下一层Layer对象,获取的分别为layers[3](输出层)、layers[2](第三层隐藏层)、layers[1](第二层隐藏层)
next_layer = self._layers[i + 1] # 得到下一层对象
# 第二步:使用 下一层Layer的weights权重 和 下一层Layer的delta中保存的 计算出当前层 delta变量的 中间变量error。
# 1.在计算layers[2](第三层隐藏层)的delta变量的 中间变量error 使用的是 layers[3](输出层)的weights权重、变量。
# Jj = j(1 − j) ∑k jk,jk即下一层输出层的next_layer.weights,即下一层输出层的next_layer.delta变量。
# ∑k jk 即为 layer.error,即为 np.dot(next_layer.weights, next_layer.delta)
# 2.在计算layers[1](第二层隐藏层)的delta变量的 中间变量error 使用的是 layers[2](第三层隐藏层)的weights权重、变量。
# = (1 − ) ∑j Jj j,j即第三层隐藏层的next_layer.weights,Jj即第三层隐藏层的next_layer.delta变量。
# ∑j Jj j 即为 layer.error,即为 np.dot(next_layer.weights, next_layer.delta)
# 3.在计算layers[0](第一层隐藏层)的delta变量的 中间变量error 使用的是 layers[1](第二层隐藏层)的weights权重、变量。
layer.error = np.dot(next_layer.weights, next_layer.delta)
# 关键步骤:计算隐藏层的 delta,参考隐藏层的梯度公式
# 第三步:last_activation为模型隐藏层的激活函数的输出值,此处即为sigmoid激活函数的输出值。
# apply_activation_derivative计算激活函数的导数,此处为计算sigmoid激活函数的导数。
# 将计算出的变量存储在 Layer类的 delta变量中,用于计算梯度。
# 1.在计算layers[2](第三层隐藏层)的delta变量:Jj = j(1 − j) ∑k jk,
# ′ = (1 − ),将()写回j形式,即变成′ = j(1 − j),j为输出层输出的预测值,
# 即apply_activation_derivative(last_activation),∑k jk 即下一层输出层Layer对象的。
# 2.在计算layers[1](第二层隐藏层)的delta变量: = (1 − ) ∑j Jj j,
# ′ = (1 − ),将()写回形式,即变成′ = (1 − ),为第三层隐藏层输出的预测值,
# 即apply_activation_derivative(last_activation),∑j Jj j 即下一层第三层隐藏层Layer对象的。
# 3.在计算layers[0](第一层隐藏层)的delta变量:。。。。。。
layer.delta = layer.error * layer.apply_activation_derivative(layer.last_activation)
# 在反向计算完每层的变量delta后,只需要按着 L/W_j = *_Jj 公式计算每层的梯度,并更新网络参数即可。
# 由于代码中的 delta 计算的是−,因此更新时使用了加号。
# 循环更新权值
for i in range(len(self._layers)): # range(4)遍历为0/1/2/3,即从第一层隐藏层开始遍历到输出层。
layer = self._layers[i] # 得到当前层对象
# atleast_xd 支持将输入数据直接视为x维。这里的 x可以表示:1,2,3。
# np.atleast_1d([1]):[1]。np.atleast_2d([1]):[[1]]。np.atleast_3d([1]):[[[1]]]。
# 第一步:o_i 为上一网络层激活函数的输出,也即为当前连接的起始节点的输出值,last_activation为激活函数的输出值。
# 1.比如为第一层隐藏层时,X使用输入层的输出作为o_i
# 2.非第一层隐藏层时,使用上一层激活函数的输出作为o_i。比如第二层隐藏层时,使用第一层激活函数的输出作为o_i;
# 第三层隐藏层时,使用第二层激活函数的输出作为o_i;输出层时,使用第第三层激活函数的输出作为o_i。
o_i = np.atleast_2d(X if i == 0 else self._layers[i - 1].last_activation)
# 梯度下降算法,delta 是公式中的负数,故这里用加号
# w1 = w1 - lr * w1_grad 优化器规则,根据 模型参数θ = θ - lr * grad 更新网络参数,grad即为此处的 L/W_j
# layer.delta * o_i.T:即为grad,即为L/W_j = _Jj*,delta即为_Jj,可以写为当前连接的起始节点的输出值与终止节点j的梯度信息_Jj的相乘运算
# 第二步:从第一层隐藏层开始逐一更新参数θ到输出层为止
# 第一层隐藏层grad:L/_ = * ,layer.delta为 = (1 − )∑j Jj j,o_i为 即上一层输入层的输出。
# 第二层隐藏层grad:L/_j = Jj * i,layer.delta为Jj = j (1 − j )∑k jk,o_i为i 即上一层第一层隐藏层的激活函数输出。
# 第三层隐藏层grad:∂L/_j = * j,layer.delta为 = (1 − )( − ) = ′( − ),
# o_i为j 即上一层第二层隐藏层的激活函数输出。输出层grad:。。。,o_i 即上一层第三层隐藏层的激活函数输出。
layer.weights += layer.delta * o_i.T * learning_rate
def train(self, X_train, X_test, y_train, y_test, learning_rate, max_epochs):
# 网络训练函数
# one-hot 编码
# 二分类任务网络设计为 2 个输出节点,因此需要将真实标签 y 进行 one-hot 编码
y_onehot = np.zeros((y_train.shape[0], 2)) # y_onehot.shape (1400, 2)
# y_train为(1400,)个标签,np.arange(y_train.shape[0])遍历从0~1399个数字,即把每个标签one-hot化为(1,2)
y_onehot[np.arange(y_train.shape[0]), y_train] = 1
# 将 one-hot 编码后的真实标签与网络的输出计算均方差,并调用反向传播函数更新网络参数,循环迭代训练集 1000 遍
mses = []
for i in range(max_epochs): # 训练 1000 个 epoch
for j in range(len(X_train)): # 一次训练一个样本
self.backpropagation(X_train[j], y_onehot[j], learning_rate)
if i % 10 == 0:
# 打印出 MSE Loss
mse = np.mean(np.square(y_onehot - self.feed_forward(X_train)))
mses.append(mse)
print('Epoch: #%s, MSE: %f' % (i, float(mse)))
# 统计并打印准确率
# print('Accuracy: %.2f%%' % (self.accuracy(self.predict(X_test), y_test.flatten()) * 100))
return mses
# 实例化网络对象,添加 4 层全连接层
nn = NeuralNetwork() # 实例化网络类
nn.add_layer(Layer(2, 25, 'sigmoid')) # 隐藏层 1, 2=>25
nn.add_layer(Layer(25, 50, 'sigmoid')) # 隐藏层 2, 25=>50
nn.add_layer(Layer(50, 25, 'sigmoid')) # 隐藏层 3, 50=>25
nn.add_layer(Layer(25, 2, 'sigmoid')) # 输出层, 25=>2
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
import seaborn as sns
from matplotlib import pyplot as plt
import numpy as np
N_SAMPLES = 2000 # 采样点数
TEST_SIZE = 0.3 # 测试数量比率
# 利用工具函数直接生成数据集
X, y = make_moons(n_samples=N_SAMPLES, noise=0.2, random_state=100)
# 将 2000 个点按着 7:3 分割为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=TEST_SIZE, random_state=42)
print(X.shape, y.shape) # (2000, 2) (2000,)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape) # (1400, 2) (600, 2) (1400,) (600,)
# 绘制数据集的分布,X 为 2D 坐标,y 为数据点的标签
def make_plot(X, y, plot_name, file_name=None, XX=None, YY=None, preds=None, dark=False):
if (dark):
plt.style.use('dark_background')
else:
sns.set_style("whitegrid")
plt.figure(figsize=(16, 12))
axes = plt.gca()
axes.set(xlabel="$x_1$", ylabel="$x_2$")
plt.title(plot_name, fontsize=30)
plt.subplots_adjust(left=0.20)
plt.subplots_adjust(right=0.80)
if (XX is not None and YY is not None and preds is not None):
plt.contourf(XX, YY, preds.reshape(XX.shape), 25, alpha=1, cmap=cm.Spectral)
plt.contour(XX, YY, preds.reshape(XX.shape), levels=[.5], cmap="Greys", vmin=0, vmax=.6)
# 绘制散点图,根据标签区分颜色
plt.scatter(X[:, 0], X[:, 1], c=y.ravel(), s=40, cmap=plt.cm.Spectral, edgecolors='none')
plt.savefig('dataset.svg')
plt.close()
# 调用 make_plot 函数绘制数据的分布,其中 X 为 2D 坐标,y 为标签
make_plot(X, y, "Classification Dataset Visualization ")
plt.show()
class Layer:
# 全连接网络层
def __init__(self, n_input, n_neurons, activation=None, weights=None, bias=None):
"""
:param int n_input: 输入节点数
:param int n_neurons: 输出节点数
:param str activation: 激活函数类型
:param weights: 权值张量,默认类内部生成
:param bias: 偏置,默认类内部生成
"""
# 通过正态分布初始化网络权值,初始化非常重要,不合适的初始化将导致网络不收敛
# weights [输入节点数,输出节点],bias [输出节点,]
self.weights = weights if weights is not None else np.random.randn(n_input, n_neurons) * np.sqrt(1 / n_neurons)
self.bias = bias if bias is not None else np.random.rand(n_neurons) * 0.1
self.activation = activation # 激活函数类型,如’sigmoid’
self.last_activation = None # 激活函数的输出值 o
self.error = None # 用于计算当前层的 delta 变量的中间变量
self.delta = None # 记录当前层的 delta 变量,用于计算梯度
# 网络层的前向传播
def activate(self, x):
# 前向传播
r = np.dot(x, self.weights) + self.bias # X@W+b
# 通过激活函数,得到全连接层的输出 o
self.last_activation = self._apply_activation(r)
return self.last_activation
# self._apply_activation 实现了不同的激活函数的前向计算过程:
def _apply_activation(self, r):
# 计算激活函数的输出
if self.activation is None:
return r # 无激活函数,直接返回
# ReLU 激活函数 () := (0, )
elif self.activation == 'relu':
return np.maximum(r, 0)
# tanh 激活函数 tanh(x)即为 2*sigmoid(2*x) - 1
elif self.activation == 'tanh':
return np.tanh(r)
# sigmoid 激活函数 1 / (1 + np.exp(-x))
elif self.activation == 'sigmoid':
return 1 / (1 + np.exp(-r))
return r
# 针对于不同的激活函数,它们的导数计算实现如下
def apply_activation_derivative(self, r):
# 计算激活函数的导数
# 无激活函数,导数为 1
if self.activation is None:
return np.ones_like(r)
# ReLU 函数的导数实现
elif self.activation == 'relu':
grad = np.array(r, copy=True) # 用于保存梯度的张量
grad[r > 0] = 1. # 元素为正的元素导数为 1
grad[r <= 0] = 0. # 元素为负的导数为 0
return grad
# tanh 函数的导数实现 1-tanh(x)**2
elif self.activation == 'tanh':
return 1 - r ** 2
# Sigmoid 函数的导数实现 sigmoid(x)*(1-sigmoid(x))
elif self.activation == 'sigmoid':
# 可以看到,Sigmoid 函数的导数实现为 ∗ (1 − ),其中即为()。
return r * (1 - r)
return r
class NeuralNetwork:
# 神经网络大类
def __init__(self):
self._layers = [] # 网络层对象列表
def add_layer(self, layer):
# 追加网络层
self._layers.append(layer)
# 网络的前向传播只需要循环调用网络层对象的前向计算函数即可
def feed_forward(self, X):
# 前向传播
for layer in self._layers:
# 依次通过各个网络层
X = layer.activate(X)
return X
"""
1.前向传播:
从前往后(从第一层隐藏层最后到输出层)
每一层中的第一步是线性函数w@x+b=z,每一层中的第二步是非线性函数(激活函数)。
最后输出层第二步激活函数的输出值作为预测值,输入到损失函数计算loss。
2.反向传播:
1.从后往前(输出层到第一层隐藏层)求每一层的delta变量
1.输出层:
= output(1 − output)(output − y) = (1 − )(y - output)
1.第一步:先计算损失函数的导数,比如此处计算均方差的导数:中间值error = 真实标签y - 预测值output,公式L/ = ( −yi),为output,yi为y。
2.第二步:然后计算激活函数的导数,比如此处计算Sigmoid的导数:output(1 − output),output为预测值,公式/ * () = (1 − )。
3.第三步:最后把损失函数导数值和激活函数导数值两者相乘得出delta变量值 = output(1 − output)(output − y) = (1 − )(y - output)。
2.最后一层隐藏层逐一计算到第一层隐藏层:
= activation(1 − activation) ∑j Jj ij
1.第一步:先计算当前层(比如第三层隐藏层)的上一层(比如输出层)的weights权重矩阵和delta变量值两者的dot矩阵相乘,
作为当前层的中间值error = np.dot(上一层weights, 上一层delta) = ∑j Jj ij,ij为上一层weights,上一层delta为Jj。
2.第二步:计算当前层激活函数的导数,比如此处计算Sigmoid的导数:activation(1 − activation),activation为激活函数输出值,公式/ * () = (1 − )。
3.第三步:最后把当前层的中间值error和激活函数导数值两者相乘得出delta变量值 = activation(1 − activation) ∑j Jj ij。
2.从前往后(第一层隐藏层到输出层)更新每一层的模型参数θ
L/θ = θ_grad = * 激活函数的输出o.T(或者输入层的输出o.T)
θ = θ - lr * θ_grad = θ - lr * L/θ
1.第一步:获取上一层网络层激活函数的输出o
1.第一层隐藏层:使用输入层的输出作为o。
2.第二层隐藏层到输出层:使用上一层网络层激活函数的输出activation作为o,比如第二层隐藏层使用第一层激活函数的输出activation作为o。
2.第二步:当前层delta变量值 * 激活函数的输出o.T(或者输入层的输出o.T) = θ_grad = L/θ
3.第三步:θ = θ - lr * θ_grad = θ - lr * L/θ:其中 L/θ表示loss对于参数θ的梯度表示为θ_grad,用于更新参数θ,lr为学习率。
"""
# 网络模型的反向传播实现稍复杂,需要从最末层开始,计算每层的变量。
# 根据我们推导的梯度公式,将计算出的变量存储在 Layer 类的 delta 变量中,用于计算梯度。
# 在 backpropagation 函数中,反向计算每层的变量,并根据梯度公式计算每层参数的梯度值,按着梯度下降算法完成一次参数的更新。
def backpropagation(self, X, y, learning_rate):
# 反向传播算法实现
# 前向计算,得到输出值
output = self.feed_forward(X)
# range(4)+reversed表示 反转从大到小遍历为 3/2/1/0,即从最后一层输出层开始从后往前遍历每一层
for i in reversed(range(len(self._layers))): # 反向循环
layer = self._layers[i] # 得到当前层对象
# 如果是输出层,获取的是layers[3]==layers[-1]
if layer == self._layers[-1]: # 对于输出层
# 计算 2分类任务的均方差的导数 L/ = ( −yi)。y为yi,即真实值;output为 ,即模型输出层的sigmoid激活函数输出的预测值
# 第一步:计算损失函数的导数,此处为使用 均方差函数的导数 计算出当前层 delta变量的 中间变量error
# = (1 − )( − ),为输出层输出的预测值,为真实值,( − )即为 y - output
layer.error = y - output
# 关键步骤:计算最后一层的 delta,参考输出层的梯度公式,此处即计算输出层所使用的sigmoid的的导数
# 第二步:apply_activation_derivative计算激活函数的导数,此处为计算sigmoid激活函数的导数,output为 模型输出层的sigmoid激活函数输出的预测值,
# 中间变量error为均方差函数的导数值,将计算出的变量存储在Layer类的delta变量中,用于计算梯度。
# = (1 − )( − ),为输出层输出的预测值,为真实值,′ = (1 − ),将()写回形式,即变成′ = (1 − ),
# (1 − )即为 apply_activation_derivative(output)
layer.delta = layer.error * layer.apply_activation_derivative(output)
# 如果是隐藏层,获取的分别为layers[2](第三层隐藏层)、layers[1](第二层隐藏层)、layers[0](第一层隐藏层)
else:
# 第一步:获取下一层Layer对象,获取的分别为layers[3](输出层)、layers[2](第三层隐藏层)、layers[1](第二层隐藏层)
next_layer = self._layers[i + 1] # 得到下一层对象
# 第二步:使用 下一层Layer的weights权重 和 下一层Layer的delta中保存的 计算出当前层 delta变量的 中间变量error。
# 1.在计算layers[2](第三层隐藏层)的delta变量的 中间变量error 使用的是 layers[3](输出层)的weights权重、变量。
# Jj = j(1 − j) ∑k jk,jk即下一层输出层的next_layer.weights,即下一层输出层的next_layer.delta变量。
# ∑k jk 即为 layer.error,即为 np.dot(next_layer.weights, next_layer.delta)
# 2.在计算layers[1](第二层隐藏层)的delta变量的 中间变量error 使用的是 layers[2](第三层隐藏层)的weights权重、变量。
# = (1 − ) ∑j Jj j,j即第三层隐藏层的next_layer.weights,Jj即第三层隐藏层的next_layer.delta变量。
# ∑j Jj j 即为 layer.error,即为 np.dot(next_layer.weights, next_layer.delta)
# 3.在计算layers[0](第一层隐藏层)的delta变量的 中间变量error 使用的是 layers[1](第二层隐藏层)的weights权重、变量。
layer.error = np.dot(next_layer.weights, next_layer.delta)
# 关键步骤:计算隐藏层的 delta,参考隐藏层的梯度公式
# 第三步:last_activation为模型隐藏层的激活函数的输出值,此处即为sigmoid激活函数的输出值。
# apply_activation_derivative计算激活函数的导数,此处为计算sigmoid激活函数的导数。
# 将计算出的变量存储在 Layer类的 delta变量中,用于计算梯度。
# 1.在计算layers[2](第三层隐藏层)的delta变量:Jj = j(1 − j) ∑k jk,
# ′ = (1 − ),将()写回j形式,即变成′ = j(1 − j),j为输出层输出的预测值,即apply_activation_derivative(last_activation),
# ∑k jk 即下一层输出层Layer对象的。
# 2.在计算layers[1](第二层隐藏层)的delta变量: = (1 − ) ∑j Jj j,
# ′ = (1 − ),将()写回形式,即变成′ = (1 − ),为第三层隐藏层输出的预测值,即apply_activation_derivative(last_activation),
# ∑j Jj j 即下一层第三层隐藏层Layer对象的。
# 3.在计算layers[0](第一层隐藏层)的delta变量:。。。。。。
layer.delta = layer.error * layer.apply_activation_derivative(layer.last_activation)
# 在反向计算完每层的变量delta后,只需要按着 L/W_j = *_Jj 公式计算每层的梯度,并更新网络参数即可。
# 由于代码中的 delta 计算的是−,因此更新时使用了加号。
# 循环更新权值
for i in range(len(self._layers)): # range(4)遍历为0/1/2/3,即从第一层隐藏层开始遍历到输出层。
layer = self._layers[i] # 得到当前层对象
# atleast_xd 支持将输入数据直接视为x维。这里的 x可以表示:1,2,3。
# np.atleast_1d([1]):[1]。np.atleast_2d([1]):[[1]]。np.atleast_3d([1]):[[[1]]]。
# 第一步:o_i 为上一网络层激活函数的输出,也即为当前连接的起始节点的输出值,last_activation为激活函数的输出值。
# 1.比如为第一层隐藏层时,X使用输入层的输出作为o_i
# 2.非第一层隐藏层时,使用上一层激活函数的输出作为o_i。比如第二层隐藏层时,使用第一层激活函数的输出作为o_i;
# 第三层隐藏层时,使用第二层激活函数的输出作为o_i;输出层时,使用第第三层激活函数的输出作为o_i。
o_i = np.atleast_2d(X if i == 0 else self._layers[i - 1].last_activation)
# 梯度下降算法,delta 是公式中的负数,故这里用加号
# w1 = w1 - lr * w1_grad 优化器规则,根据 模型参数θ = θ - lr * grad 更新网络参数,grad即为此处的 L/W_j
# layer.delta * o_i.T:即为grad,即为L/W_j = _Jj*,delta即为_Jj,可以写为当前连接的起始节点的输出值与终止节点j的梯度信息_Jj的相乘运算
# 第二步:从第一层隐藏层开始逐一更新参数θ到输出层为止
# 第一层隐藏层grad:L/_ = * ,layer.delta为 = (1 − )∑j Jj j,o_i为 即上一层输入层的输出。
# 第二层隐藏层grad:L/_j = Jj * i,layer.delta为Jj = j (1 − j )∑k jk,o_i为i 即上一层第一层隐藏层的激活函数输出。
# 第三层隐藏层grad:∂L/_j = * j,layer.delta为 = (1 − )( − ) = ′( − ),o_i为j 即上一层第二层隐藏层的激活函数输出。
# 输出层grad:。。。,o_i 即上一层第三层隐藏层的激活函数输出。
layer.weights += layer.delta * o_i.T * learning_rate
def train(self, X_train, X_test, y_train, y_test, learning_rate, max_epochs):
# 网络训练函数
# one-hot 编码
# 二分类任务网络设计为 2 个输出节点,因此需要将真实标签 y 进行 one-hot 编码
y_onehot = np.zeros((y_train.shape[0], 2)) # y_onehot.shape (1400, 2)
# y_train为(1400,)个标签,np.arange(y_train.shape[0])遍历从0~1399个数字,即把每个标签one-hot化为(1,2)
y_onehot[np.arange(y_train.shape[0]), y_train] = 1
# 将 one-hot 编码后的真实标签与网络的输出计算均方差,并调用反向传播函数更新网络参数,循环迭代训练集 1000 遍
mses = []
for i in range(max_epochs): # 训练 1000 个 epoch
for j in range(len(X_train)): # 一次训练一个样本
self.backpropagation(X_train[j], y_onehot[j], learning_rate)
if i % 10 == 0:
# 打印出 MSE Loss
mse = np.mean(np.square(y_onehot - self.feed_forward(X_train)))
mses.append(mse)
print('Epoch: #%s, MSE: %f' % (i, float(mse)))
# 统计并打印准确率
# print('Accuracy: %.2f%%' % (self.accuracy(self.predict(X_test), y_test.flatten()) * 100))
return mses
# 实例化网络对象,添加 4 层全连接层:
nn = NeuralNetwork() # 实例化网络类
nn.add_layer(Layer(2, 25, 'sigmoid')) # 隐藏层 1, 2=>25
nn.add_layer(Layer(25, 50, 'sigmoid')) # 隐藏层 2, 25=>50
nn.add_layer(Layer(50, 25, 'sigmoid')) # 隐藏层 3, 50=>25
nn.add_layer(Layer(25, 2, 'sigmoid')) # 输出层, 25=>2
nn.train(X_train, X_test, y_train, y_test, 0.01, 1000)