OpenGL学习脚印：伽马校正(Gamma Correction)

写在前面
由于CRT,LED等显示设备显示颜色时并非按照线性方式工作，因此我们在程序中输出的颜色，最终输出到显示器上时会产生亮度减弱的现象，这种现象在计算光照和实时渲染时对图形质量有一定影响，需要我们加以处理。本节将熟悉Gamma校正的概念，并通过点光源的示例来表现Gamma校正对图形效果的影响。本节示例代码均可以在我的github下载。

为什么需要 γ 校正

我们在图形程序中认为(1.0, 0.0,0.0)颜色应该是(0.5,0.0, 0.0)的红色强度的2倍，但是实际上在显示设备上对于输入的原始值，并不按照线性的关系来反映这个亮度差别。显示设备对于输入的原始值，按照一种非线性的方式处理，也就是说上面原始值中红色分量提高2倍时，实际处理时得到的亮度并不是成这种2倍的比例。

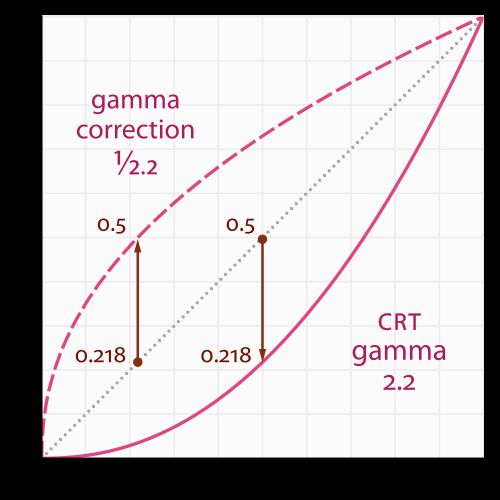
事实上，CRT、LED这类显示设备，对于输入的原始值，会计算一个指数函数，即： Cout=C2.2in 。这里的2.2称为 伽马系数(Gamma factor)，范围一般在2.0到2.4之间，不同显示器这个系数有区别。这个关系如下图所示（来自Gamma Correction）：

上面的图中间的点线，是我们图形中工作的线性颜色，当显示器接受这个线性原始值后，进行了上面的指数计算，将会输出图中下方的实线所示的非线性的颜色，亮度会降低。对于0。0和1.0两个值显示器总是原样输出，两个值之间的颜色亮度将会降低。

因此，要想最终显示器按照我们预期的输出中间的线性颜色，我们就需要执行上述指数运算的逆运算： Ccorrected=C1.0/2.2out ，这样最终输出颜色，才会是我们在图形应用中指定的颜色。 执行这个逆运算的过程，称之为伽马校正(Gamma Correction)，一般的取伽马系数2.2进行校正产生的效果在大多数显示器上都比较理想，实际还可以根据显示器不同进行查询。例如上面的颜色(0.5,0.0,0.0)执行校正后的值为：

(0.5,0.0,0.0)1/2.2=(0.5,0.0,0.0)0.45=(0.73,0.0,0.0)
则实际显示为：
(0.73,0.0,0.0)2.2=(0.5,0.0,0.0)
也就是说要让显示器显示我们预期的 (0.5,0.0,0.0) ，我们的着色器需要输出 (0.73,0.0,0.0) 。

另外一个需要知道的事实时，大多数的图片在显示器已经被预处理过了，因此存储的颜色信息已经是伽马校正了的，我们在处理纹理时需要工作在线性的颜色空间下，因此需要对输入的图片，例如JPEG纹理进行处理，保证它在线性颜色空间下。关于实际操作，后面会介绍。

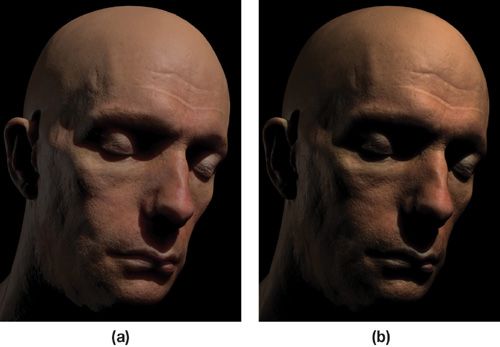
有了上面的基础，我们直观感受下，有无伽马校正，下面是绘制人面皮肤的效果图，图形对比如下(来自The Importance of Being Linear)：

上面的左图中，将输入的纹理进行了线性处理，同时最终输出时进行了伽马校正；而右边的图形两个处理都没有进行，因而面部的镜面光加上漫反射光后变成了黄色，同时面部的阴影变得太暗了。

处理输入的纹理

对于输入的纹理图片，由于大多数情况下已经进行了伽马校正，因此我们要得到他们线性的颜色，必须去除这个校正，在OpenGL中提供了两种方式。

方式一是通过在构造纹理对象时，指明纹理的内部格式为sRGB或者GL_SRGB_ALPHA，SRGB就是我们所说的已经校正后的非线性颜色，当按上述方式指明时OpenGL将会自动将其转换到线性空间。

   glTexImage2D(GL_TEXTURE_2D, 0, GL_SRGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, image); 

方式二是在着色器中开始使用纹理时，手动执行转换：

float gamma = 2.2;
vec3 diffuseColor = pow(texture(diffuse, texCoords).rgb, vec3(gamma));

这种方式是在着色器中执行伽马变换的逆操作，相比上一种方式，显得麻烦些。

需要注意的是，对于某些类型的纹理，例如diffuse map，通常已经工作在线性空间了，这个时候就不需要指明为sRGB格式了。在指明为sRGB格式时也需要根据不同情况加以区别。

处理着色器的输出

对于着色器的输出，我们有两种方式执行伽马校正。第一种方式，即采用OpenGL提供的FBO的选项，当开启 GL_FRAMEBUFFER_SRGB选项后，随后的所有FBO绘制将自动执行校正，包括默认的FBO。

glEnable(GL_FRAMEBUFFER_SRGB); 

当开启这个选项后，执行的伽马校正，通常是2.2的校正。需要注意的是，如果你使用多个FBO来完成某项操作，当需要在中间步骤中使用线性颜色空间时，就需要关闭这个选项，否则将会在错误的颜色空间上工作。一般是在最后一个FBO上操作时开启这个选项。

第二种方式是在着色器的输出中，手动进行伽马校正：

   vec3 result;
   result = pow(result, vec3(1.0 / 2.2));   // 启用Gamma校正

注意上面的pow函数输入为vec3时，将会分别为每个分量计算指数值。

有了上面的基础后，我们下面通过编写程序对比下处理伽马校正的效果。

伽马校正处理的效果对比

首先我们分别让纹理和最终输出的颜色在线性和非线性空间上进行一个对比，下面的图中组合了4种方式，渲染了我们熟悉的纳米战斗服模型，对比效果如下：

图中a图是我们之前的处理方式，纹理按照格式GL_RGB输入，则工作在非线性空间，同时着色器未进行伽马校正，这个效果是我们能接受的；图b我们对纹理的伽马操作进行了还原让其工作在线性空间，着色器同样未进行伽马校正，那么由于输出的线性颜色经过伽马系数的指数运算后，降低了亮度，变得很暗；图c中，我们对纹理的伽马校正进行了还原，纹理工作在线性空间，最终着色器输出进行了伽马校正，因此效果正常，同图a相比，有少许差别，伽马校正有些时候效果不一定非常明显。图d中由于纹理未进行伽马校正的逆操作，同时着色器输出又再次进行了伽马校正，相当于进行了两次伽马校正，因此亮度变得很大，这个就严重失真了。

同时如果考虑到光的衰减，我们在光源类型一节提到过，可以使用线性衰减函数或者二次衰减函数，对于这两个函数，着色器进行伽马校正和不进行伽马校正，效果对比如下：

这个例子参考自www.learnopengl.com Gamma Correction。当未进行伽马校正时，线性衰减函数的效果比二次衰减函数的好，因为：

(1/distance)2.2 比 (1/distance2)2.2 更接近实际物理上的二次衰减情形。

当进行了伽马校正时，二次衰减函数效果比线性衰减函数好，因为：
((1/distance2)1/2.2)2.2=(1/distance2) 比
((1/distance)1/2.2)2.2=(1/distance) 更接近物理上的二次衰减情形。这个例子说明了伽马校正对光照模型计算的一个影响，需要引起我们的注意。

参考资料

1.Color space linearity and gamma correction
2.Modern OpenGL 07 – More Lighting: Ambient, Specular, Attenuation, Gamma
3.Gamma Correction: A Story of Linearity
4.Chapter 24. The Importance of Being Linear