计算智能——BP神经网络和感知器的简单应用
文章目录
- 神经网络基本原理
- 1.人工神经元模型
- 2.BP神经网络模型：前馈式
- 3.BP神经网络训练过程
- 4.BP神经网络算法
- BP神经网络的实现
- 1.代码
- 2.部分代码解释
- 3.运行结果
- 4.小结
- 感知器
- 1.代码
- 2.部分代码解释
- 3.运行结果
- 4.小结
神经网络基本原理
人工神经网络无需事先确定输入输出之间映射关系的数学方程，仅通过自身的训练，学习某种规则，在给定输入值时得到最接近期望输出值的结果。作为一种智能信息处理系统，人工神经网络实现其功能的核心是算法。BP神经网络是一种按误差反向传播(简称误差反传)训练的多层前馈网络，其算法称为BP算法，它的基本思想是梯度下降法，利用梯度搜索技术，以期使网络的实际输出值和期望输出值的误差均方差为最小。
1.人工神经元模型
图中x1~xn是从其他神经元传来的输入信号，wij表示表示从神经元j到神经元i的连接权值，θ表示一个阈值 ( threshold )，或称为偏置( bias )。则神经元i的输出与输入的关系表示为：
图中 yi表示神经元i的输出，函数f称为激活函数，net称为净激活。
若神经元的neti为正，称该神经元处于激活状态或兴奋状态，若neti为负，则称神经元处于抑制状态。
2.BP神经网络模型：前馈式
前馈网络也称前向网络。这种网络只在训练过程会有反馈信号，而在分类过程中数据只能向前传送，直到到达输出层，层间没有向后的反馈信号，因此被称为前馈网络。感知机与BP神经网络就属于前馈网络。
如下是一个3层的前馈神经网络，其中第一层是输入单元，第二层称为隐含层，第三层称为输出层。
设网络输入为x，则隐含层第j个节点输入为：
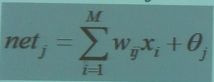
输出层第k个节点输入为：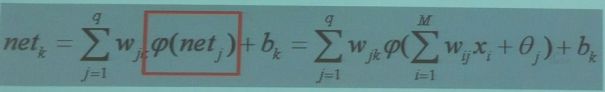
输出层第k个节点输出为：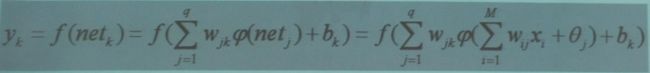
3.BP神经网络训练过程
网络学习的目的就是根据训练数据的误差E对于各个参数的梯度，求解参数调整量
神经网络结构：
参数调整量：
4.BP神经网络算法
输入：网络结构参数（层数、节点数等）；训练的数据集
输出：网络权值与阈值
1.网络权值初始化
2.对输入训练S={(x1,t1),(x2,t2),…,(xK,tK)}，依次通过输入层、隐含层、输出层，分别计算误差E
3.通过误差E反传计算每一个神经元的误差信号
4.根据误差信号调整网络权值W和节点阈值b
5.对训练数据不断迭代，直至最大迭代次数或误差低于某一阈值为止
（训练过程可采用随机梯度下降和批量梯度下降）
BP神经网络的实现
1.代码
% BP网络
% BP神经网络的构建
net=newff([-1 2;0 5],[3,1],{'tansig','purelin'},'traingd')
net.IW{1}
net.b{1}
p=[1;2];
a=sim(net,p)
net=init(net);
net.IW{1}
net.b{1}
a=sim(net,p)
%net.IW{1}*p+net.b{1}
p2=net.IW{1}*p+net.b{1}
a2=sign(p2)
a3=tansig(a2)
a4=purelin(a3)
net.b{2}
net.b{1}
net.IW{1}
net.IW{2}
0.7616+net.b{2}
a-net.b{2}
(a-net.b{2})/ 0.7616
help purelin
p1=[0;0];
a5=sim(net,p1)
net.b{2}
% BP网络
% BP神经网络的构建
net=newff([-1 2;0 5],[3,1],{'tansig','purelin'},'traingd')
net.IW{1}
net.b{1}
%p=[1;];
p=[1;2];
a=sim(net,p)
net=init(net);
net.IW{1}
net.b{1}
a=sim(net,p)
net.IW{1}*p+net.b{1}
p2=net.IW{1}*p+net.b{1}
a2=sign(p2)
a3=tansig(a2)
a4=purelin(a3)
net.b{2}
net.b{1}
P=[1.2;3;0.5;1.6]
W=[0.3 0.6 0.1 0.8]
net1=newp([0 2;0 2;0 2;0 2],1,'purelin');
net2=newp([0 2;0 2;0 2;0 2],1,'logsig');
net3=newp([0 2;0 2;0 2;0 2],1,'tansig');
net4=newp([0 2;0 2;0 2;0 2],1,'hardlim');
net1.IW{1}
net2.IW{1}
net3.IW{1}
net4.IW{1}
net1.b{1}
net2.b{1}
net3.b{1}
net4.b{1}
net1.IW{1}=W;
net2.IW{1}=W;
net3.IW{1}=W;
net4.IW{1}=W;
a1=sim(net1,P)
a2=sim(net2,P)
a3=sim(net3,P)
a4=sim(net4,P)
init(net1);
net1.b{1}
help tansig
% 训练
p=[-0.1 0.5]
t=[-0.3 0.4]
w_range=-2:0.4:2;
b_range=-2:0.4:2;
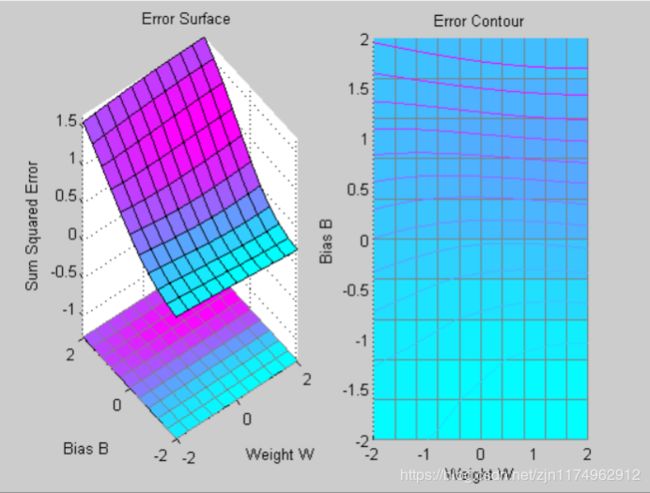
ES=errsurf(p,t,w_range,b_range,'logsig');%单输入神经元的误差曲面
plotes(w_range,b_range,ES)%绘制单输入神经元的误差曲面
pause(0.5);
hold off;
net=newp([-2,2],1,'logsig');
net.trainparam.epochs=100;
net.trainparam.goal=0.001;
figure(2);
[net,tr]=train(net,p,t);
title('动态逼近')
wight=net.iw{1}
bias=net.b
pause;
close;
% 练
p=[-0.2 0.2 0.3 0.4]
t=[-0.9 -0.2 1.2 2.0]
h1=figure(1);
net=newff([-2,2],[5,1],{'tansig','purelin'},'trainlm');
net.trainparam.epochs=100;
net.trainparam.goal=0.0001;
net=train(net,p,t);
a1=sim(net,p)
pause;
h2=figure(2);
plot(p,t,'*');
title('样本')
title('样本');
xlabel('Input');
ylabel('Output');
pause;
hold on;
ptest1=[0.2 0.1]
ptest2=[0.2 0.1 0.9]
a1=sim(net,ptest1);
a2=sim(net,ptest2);
net.iw{1}
net.iw{2}
net.b{1}
net.b{2}
2.部分代码解释
1 net=newff([-1 2;0 5],[3,1],{‘tansig’,‘purelin’},‘traingd’)
（1）newff函数语法语法：net = newff ( A, B, {C} ,‘trainFun’)
参数：A：一个n×2的矩阵，第i行元素为输入信号xi的最小值和最大值；
B：一个k维行向量，其元素为网络中各层节点数；
C：一个k维字符串行向量，每一分量为对应层神经元的激活函数；
trainFun ：为学习规则采用的训练算法。
（2）常用的激活函数
a) 线性函数 f(x) = x
该函数的字符串为’purelin’
b) 对数S形转移函数
该函数的字符串为’logsig’
c) 双曲正切S形函数
该函数的字符串为’ tansig
（3）常见的训练函数
traingd ：梯度下降BP训练函数
traingdx ：梯度下降自适应学习率训练函数
这里A对应一个2行2列的矩阵，有两个输入信号，x1的最小值为-1，最大值为2，x2的最小值为0，最大值为5；
B对应一个2维行向量，表示第一层有3个节点，第二层有1个节点；
C表示第一层神经元的激活函数为双曲正切S形函数，第二层神经元的激活函数为线性函数；
训练算法为梯度下降BP训练函数。
2 net.IW{1}
net.b{1}
权值/阈值
net.iw % 权值元包：net.iw{1}：当网络只有一层时，net.iw是一个1x1的cell；net.iw{1,1}：当网络有多层时，net.iw是一个元包矩阵，net.iw{1}表示W0，输入层到隐含层之间的权值。
net.b % 阈值/偏置值，net.b{1}表示隐含层的阈值
3 a=sim(net,p)
sim函数
sim ：使用网络进行仿真预测 评估给定输入的网络输出
语法：Y=sim(net,X)
参数：net：网络
Y是训练好的网络net对输入X的实际输出
p=[1;2] 所以输入1，2
4 net=init(net);
自定义初始化网络
5 p2=net.IW{1}*p+net.b{1}
p2为隐含层输入
6 a2=sign(p2)
a3=tansig(a2)
a4=purelin(a3)
a2、a3、a4分别用三个不同激活函数激活
7 0.7616+net.b{2} 输出层输出
0.7616+net.b{2}=1.6806
a-net.b{2}
(a-net.b{2})/ 0.7616
a-net.b{2}= 0.7683
(a-net.b{2})/ 0.7616=1.0088
8 net1=newp([0 2;0 2;0 2;0 2],1,‘purelin’);
函数newp用来生成一个感知器神经网络
net=newp(pr,s,tf,lf);
net：表示生成的感知器网络
pr：一个R*2矩阵，由R维输入向量的每维最小值和最大值组成
s：神经元个数
tf：感知器的传递/激活函数，默认为hardlim
lf：感知器的学习修正函数，默认为learnp
9 net.trainparam.goal ：神经网络训练的目标误差
net.trainparam.epochs ：最大迭代次数
10 [net,tr]=train(net,p,t)
网络训练学习函数。
语法：[ net, tr, Y1, E ] = train( net, X, Y )
参数：X：网络实际输入
Y：网络应有输出
tr：训练跟踪信息
Y1：网络实际输出
E：误差矩阵
11 wight=net.iw{1}
bias=net.b
训练后的权值和阈值
wight = 15.1653
bias = [-8.8694]
3.运行结果
net=newff([-1 2;0 5],[3,1],{‘tansig’,‘purelin’},‘traingd’)
网络创建完成之后输出信息：
net = Neural Network %神经网络
name: 'Custom Neural Network'
userdata: (your custom info)
dimensions: %维度
numInputs: 1
numLayers: 2
numOutputs: 1
numInputDelays: 0
numLayerDelays: 0
numFeedbackDelays: 0
numWeightElements: 13
sampleTime: 1
connections: %连接
biasConnect: [1; 1]
inputConnect: [1; 0]
layerConnect: [0 0; 1 0]
outputConnect: [0 1]
subobjects: %子对象
input: Equivalent to inputs{1}
output: Equivalent to outputs{2}
inputs: {1x1 cell array of 1 input}
layers: {2x1 cell array of 2 layers}
outputs: {1x2 cell array of 1 output}
biases: {2x1 cell array of 2 biases}
inputWeights: {2x1 cell array of 1 weight}
layerWeights: {2x2 cell array of 1 weight}
functions: %函数
adaptFcn: 'adaptwb'
adaptParam: (none)
derivFcn: 'defaultderiv'
divideFcn: (none)
divideParam: (none)
divideMode: 'sample'
initFcn: 'initlay'
performFcn: 'mse'
performParam: .regularization, .normalization
plotFcns: {'plotperform', plottrainstate,
plotregression}
plotParams: {1x3 cell array of 3 params}
trainFcn: 'traingd'
trainParam: .showWindow, .showCommandLine, .show, .epochs,
.time, .goal, .min_grad, .max_fail, .lr
weight and bias values: %权重和阈值
IW: {2x1 cell} containing 1 input weight matrix
LW: {2x2 cell} containing 1 layer weight matrix
b: {2x1 cell} containing 2 bias vectors
methods: %方法
adapt: Learn while in continuous use
configure: Configure inputs & outputs
gensim: Generate Simulink model
init: Initialize weights & biases
perform: Calculate performance
sim: Evaluate network outputs given inputs
train: Train network with examples
view: View diagram
unconfigure: Unconfigure inputs & outputs
部分阈值权值输出的结果：
L4、L5：
net.IW{1}=0.9793 0.7717
1.5369 0.3008
-1.0989 -0.7114
net.b{1}= -4.8438
-1.5204
-0.0970
L10、11：
net.IW{1}=-1.6151 -0.0414
1.3628 0.5217
1.2726 -0.5981
net.b{1}=3.3359
-1.9858
3.2839
部分仿真结果：
第一次 a=0.5105
第二次 a=1.6873
输入p1=[0;0] 仿真结果为a5
a5=0.5450
net1.IW{1}=0 0 0 0
net2.IW{1}=0 0 0 0
net3.IW{1}=0 0 0 0
net4.IW{1}=0 0 0 0
net1.b{1}=0
net2.b{1}=0
net3.b{1}=0
net4.b{1}=0
使用网络net1、net2、net3、net4对输入P仿真预测
a1 =3.4900
a2 =0.9704
a3 =0.9981
a4 =1
第二次训练后再对net网络仿真预测，得到权值和阈值
net.iw{1}=-3.5000
-9.9216
1.3371
3.4355
-3.5000
net.iw{2}=[]
net.b{1}=6.9999
2.6001
-9.4693
3.7257
-6.9999
net.b{2}=0.1956
隐含层输入p2
p2=1.6380
0.4205
3.3602
a2、a3、a4激活函数之后：
a2 = 1
1
1
a3 = 0.7616
0.7616
0.7616
a4 = 0.7616
0.7616
0.7616
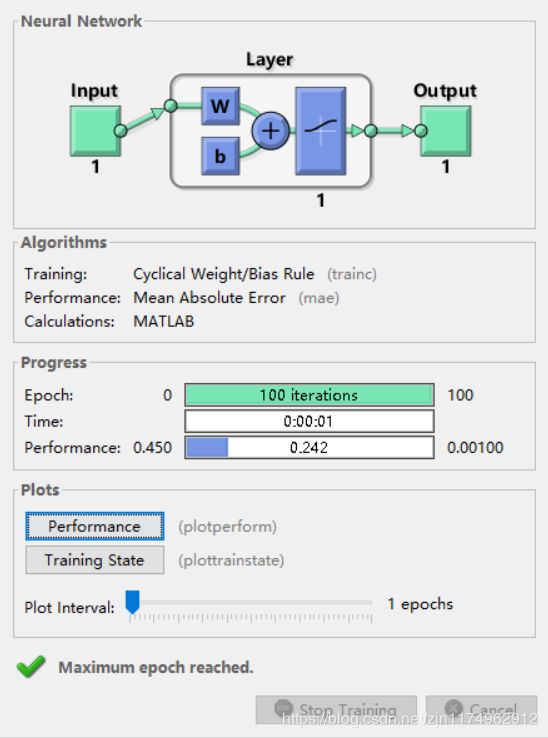
第二部分显示的是训练算法，这里为 trainc - 循环顺序权重/阈值的训练；误差指标为MAE
第三部分显示训练进度：
Epoch：训练次数；在其右边显示的是最大的训练次数，可以设定，上面例子中设为100；而进度条中显示的是实际训练的次数，上面例子中实际训练次数为100次。
Time：训练时间，也就是本次训练中，使用的时间
Performance：性能指标；本例子中为平均绝对误差(mae)的最大值。精度条中显示的是当前的平均绝对误差；进度条右边显示的是设定的平均绝对误差(如果当前的平均绝对误差小于设定值，则停止训练)，这个指标可以用.trainParam.goal参数设定。
第四部分为作图。分别点击两个按钮能看到误差变化曲线，分别用于绘制当前神经网络的性能图，训练状态。
性能图：
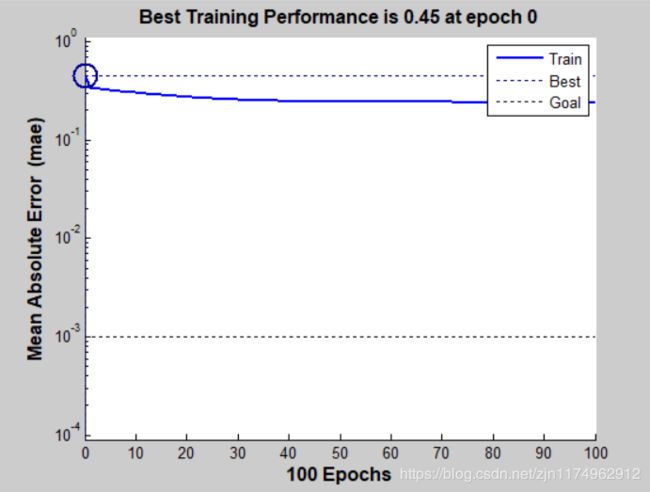
第一部分图形化的结构，这里是1输入，1输出，中间两个隐藏层，第一层5个结点 第二次1个节点
第二部分显示的是训练算法，这里是trainlm - 采用Levenberg -马奎德反向传递；好处就是在于可以调节: 如果下降太快，使用较小的λ，使之更接近高斯牛顿法 ； 如果下降太慢，使用较大的λ，使之更接近梯度下降法；误差指标为mse
第三部分显示训练进度：
Epoch：训练次数；在其右边显示的是最大的训练次数，可以设定，上面例子中设为100；而进度条中显示的是实际训练的次数，上面例子中实际训练次数为8次。
Time：训练时间，也就是本次训练中，使用的时间
Performance：性能指标；本例子中为均方误差(mse)的最大值。精度条中显示的是当前的均方误差；进度条右边显示的是设定的均方误差(如果当前的均方误差小于设定值，则停止训练)，这个指标可以用.trainParam.goal参数设定。Gradiengt：梯度2；进度条中显示的当前的梯度值，其右边显示的是设定的梯度值。如果当前的梯度值达到了设定值，则停止训练。
Mu: trainParam这个结构体的参数，确定学习根据牛顿法还是梯度法
validation check为泛化能力检查（若连续6次训练误差不降反升，则强行结束训练）
第四部分为作图。分别点击三个按钮能看到误差变化曲线，分别用于绘制当前神经网络的性能图，训练状态和回归分析。
性能图：
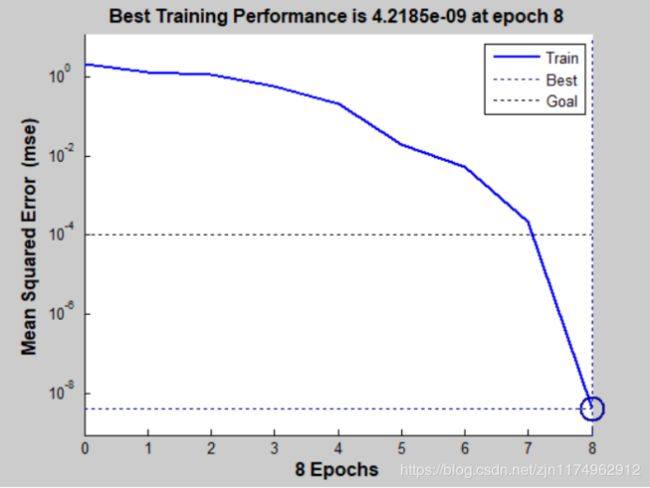
训练状态：
回归分析：
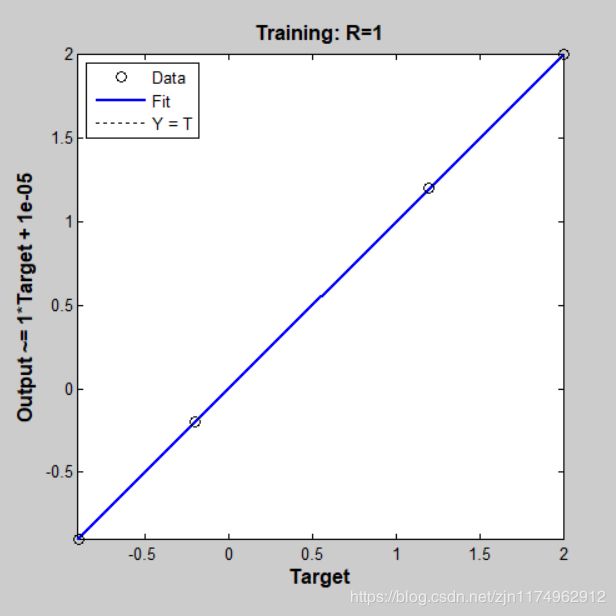
绘制输入输出样本点的坐标图：
运行完成之后的工作区：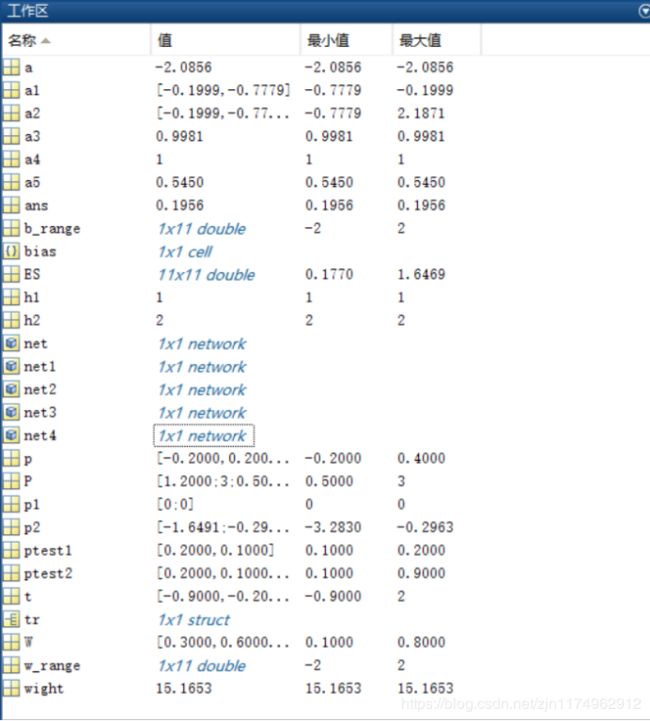
4.小结
BP算法存在的问题：
（1）梯度越来越稀疏：从顶层越往下，误差校正信号越来越小；
（2）收敛到局部最小值：尤其是从远离最优区域开始的时候（随机值初始化会导致这种情况的发生）；
（3）一般，我们只能用有标签的数据来训练：但大部分的数据是没标签的，而大脑可以从没有标签的的数据中学习；
感知器
1.代码
% 第一章 感知器
% 1. 感知器神经网络的构建
% 1.1 生成网络
net=newp([0 2],1);%单输入，输入值为[0,2]之间的数
inputweights=net.inputweights{1,1};%第一层的权重为1
biases=net.biases{1};%阈值为1
% 1.2 网络仿真
net=newp([-2 2;-2 2],1);%两个输入，一个神经元，默认二值激活
net.IW{1,1}=[-1 1];%权重，net.IW{i,j}表示第i层网络第j个神经元的权重向量
net.IW{1,1}
net.b{1}=1;
net.b{1}
p1=[1;1],a1=sim(net,p1)
p2=[1;-1],a2=sim(net,p2)
p3={[1;1] [1 ;-1]},a3=sim(net,p3) %两组数据放一起
p4=[1 1;1 -1],a4=sim(net,p4)%也可以放在矩阵里面
net.IW{1,1}=[3,4];
net.b{1}=[1];
a1=sim(net,p1)
% 1.3 网络初始化
net=init(net);
wts=net.IW{1,1}
bias=net.b{1}
% 改变权值和阈值为随机数
net.inputweights{1,1}.initFcn='rands';
net.biases{1}.initFcn='rands';
net=init(net);
bias=net.b{1}
wts=net.IW{1,1}
a1=sim(net,p1)
% 2. 感知器神经网络的学习和训练
% 1 网络学习
net=newp([-2 2;-2 2],1);
net.b{1}=[0];
w=[1 -0.8]
net.IW{1,1}=w;
p=[1;2];
t=[1];
a=sim(net,p)
e=t-a
help learnp
dw=learnp(w,p,[],[],[],[],e,[],[],[],[],[])
w=w+dw
net.IW{1,1}=w;
a=sim(net,p)
net = newp([0 1; -2 2],1);
P = [0 0 1 1; 0 1 0 1];
T = [0 1 1 1];
Y = sim(net,P)
net.trainParam.epochs = 20;
net = train(net,P,T);
Y = sim(net,P)
% 2 网络训练
net=init(net);
p1=[2;2];t1=0;p2=[1;-2];t2=1;p3=[-2;2];t3=0;p4=[-1;1];t4=1;
net.trainParam.epochs=1;
net=train(net,p1,t1)
w=net.IW{1,1}
b=net.b{1}
a=sim(net,p1)
net=init(net);
p=[[2;2] [1;-2] [-2;2] [-1;1]];
t=[0 1 0 1];
net.trainParam.epochs=1;
net=train(net,p,t);
a=sim(net,p)
net=init(net);
net.trainParam.epochs=2;
net=train(net,p,t);
a=sim(net,p)
net=init(net);
net.trainParam.epochs=20;
net=train(net,p,t);
a=sim(net,p)
% 3. 二输入感知器分类可视化问题
P=[-0.5 1 0.5 -0.1;-0.5 1 -0.5 1];
T=[1 1 0 1]
net=newp([-1 1;-1 1],1);
plotpv(P,T);
plotpc(net.IW{1,1},net.b{1});
%hold on;
%plotpv(P,T);
net=adapt(net,P,T);
net.IW{1,1}
net.b{1}
plotpv(P,T);
plotpc(net.IW{1,1},net.b{1})
net.adaptParam.passes=3;
net=adapt(net,P,T);
net.IW{1,1}
net.b{1}
plotpc(net.IW{1},net.b{1})
net.adaptParam.passes=6;
net=adapt(net,P,T)
net.IW{1,1}
net.b{1}
plotpv(P,T);
plotpc(net.IW{1},net.b{1})
plotpc(net.IW{1},net.b{1})
%仿真
a=sim(net,p);
plotpv(p,a)
p=[0.7;1.2]
a=sim(net,p);
plotpv(p,a);
hold on;
plotpv(P,T);
plotpc(net.IW{1},net.b{1})
%感知器能够正确分类，从而网络可行。
% 4. 标准化学习规则训练奇异样本
P=[-0.5 -0.5 0.3 -0.1 -40;-0.5 0.5 -0.5 1.0 50]
T=[1 1 0 0 1];
net=newp([-40 1;-1 50],1);
plotpv(P,T);%标出所有点
hold on;
linehandle=plotpc(net.IW{1},net.b{1});%画出分类线
E=1;
net.adaptParam.passes=3;%passes决定在训练过程中训练值重复的次数。
while (sse(E))
[net,Y,E]=adapt(net,P,T);
linehandle=plotpc(net.IW{1},net.b{1},linehandle);
drawnow;
end;
axis([-2 2 -2 2]);
net.IW{1}
net.b{1}
%另外一种网络修正学习（非标准化学习规则learnp）
hold off;
net=init(net);
net.adaptParam.passes=3;
net=adapt(net,P,T);
plotpc(net.IW{1},net.b{1});
axis([-2 2 -2 2]);
net.IW{1}
net.b{1}
%无法正确分类
%标准化学习规则网络训练速度要快！
% 训练奇异样本
% 用标准化感知器学习规则（标准化学习数learnpn）进行分类
net=newp([-40 1;-1 50],1,'hardlim','learnpn');
plotpv(P,T);
linehandle=plotpc(net.IW{1},net.b{1});
e=1;
net.adaptParam.passes=3;
net=init(net);
linehandle=plotpc(net.IW{1},net.b{1});
while (sse(e))
[net,Y,e]=adapt(net,P,T);
linehandle=plotpc(net.IW{1},net.b{1},linehandle);
end;
axis([-2 2 -2 2]);
net.IW{1}%权重
net.b{1}%阈值
%正确分类
%非标准化感知器学习规则训练奇异样本的结果
net=newp([-40 1;-1 50],1);
net.trainParam.epochs=30;
net=train(net,P,T);
pause;
linehandle=plotpc(net.IW{1},net.b{1});
hold on;
plotpv(P,T);
linehandle=plotpc(net.IW{1},net.b{1});
axis([-2 2 -2 2]);
% 5. 设计多个感知器神经元解决分类问题
p=[1.0 1.2 2.0 -0.8; 2.0 0.9 -0.5 0.7]
t=[1 1 0 1;0 1 1 0]
plotpv(p,t);
hold on;
net=newp([-0.8 1.2; -0.5 2.0],2);
linehandle=plotpc(net.IW{1},net.b{1});
net=newp([-0.8 1.2; -0.5 2.0],2);
linehandle=plotpc(net.IW{1},net.b{1});
e=1;
net=init(net);
while (sse(e))
[net,y,e]=adapt(net,p,t);
linehandle=plotpc(net.IW{1},net.b{1},linehandle);
drawnow;
end;
2.部分代码解释
1 dw=learnp(w,p,[],[],[],[],e,[],[],[],[],[])
learnp是感知器重量/偏差学习功能
dw=learnp(W,P,Z,N,A,T,E,D,gW,gA,LP,LS)
dw - 权值或阈值的增量矩阵
W - SxR权重矩阵（或b，Sx1偏差向量）。
P - RxQ输入向量（或（1，Q））。
Z - SxQ加权输入向量。
N - SxQnet输入向量。
A - SxQ输出向量。
T - SxQ层目标向量。
E - SxQ层误差向量。
gW - 相对于性能的SxR梯度。
gA - SxQ输出梯度与性能有关。
D - SxS神经元距离。
LP - 学习参数，无，LP = []。
LS - 学习状态，最初应为= []
2 plotpv(P,T);
plotpv函数：用于在坐标轴中绘制给定的样本点及其类别
3 plotpc(net.IW{1,1},net.b{1});
plotpc函数：用于绘制感知器的分界线
4 net=adapt(net,P,T);
adapt既可以实现批训练，也可以实现增长训练，主要取决于神经网络的输入形式是并行输入（concurrent inputs）还是串行输入（sequential inputs），如果是前者则实现批训练，如果后者则是增长训练
如果用train来训练网络则是批训练
批训练是指当全部输入都输入神经网络后，其权值和阀值才更新一次。而增长训练是指每输入一个输入，权值和阀值就更新一次
并行输入，其格式是用数组[]的形式来表示。即[1 2,3 4]这个就是并行输入，其输入不分先后。而串行输入则是用细胞数组{}来表示，如{[1;3],[2;4]}，其输入有先后顺序
5 net.adaptParam.passes=3;
最大训练次数
passes决定在训练过程中训练值重复的次数
6 奇异样本
当网络的输入样本中存在奇异样本时（即该样本向量相对其他所有样本向量特别大或特别小），此时网络训练时间将大大增加
7 sse(E)
sse函数是用来判定误差E的函数
sse()是神经网络工具箱中求网络误差平方和的函数
8 net=newp([-40 1;-1 50],1,‘hardlim’,‘learnpn’);
常用的阈值函数：
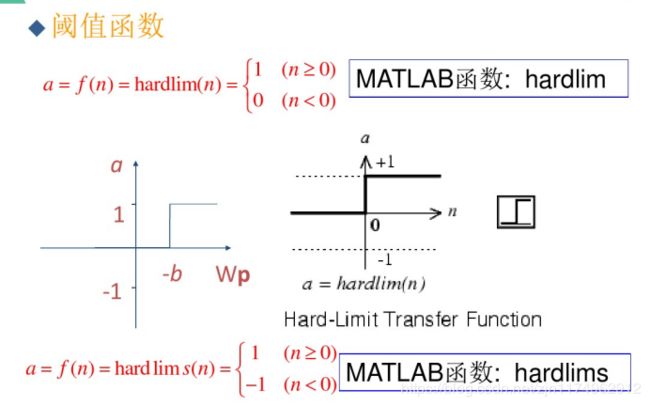
常用的权值和阈值学习函数：
9 [net,Y,e]=adapt(net,P,T)
返回实际输出和误差矩阵
3.运行结果
net=newp([-2 2;-2 2],1);%两个输入，一个神经元，默认二值激活
p1=[1;1],a1=sim(net,p1)
p2=[1;-1],a2=sim(net,p2)
p3={[1;1] ，[1 ;-1]},a3=sim(net,p3) %两组数据放一起
p4=[1 1;1 -1],a4=sim(net,p4)%也可以放在矩阵里面
创建网络后运用不同输入进行网络仿真：
p1 =
1
1
a1 =
1
p2 =
1
-1
a2 =
0
p3 =
[2x1 double] [2x1 double]
a3 =
[1] [0]
p4 =
1 1
1 -1
a4 =
1 0
网络初始化
net=init(net);
wts=net.IW{1,1}
bias=net.b{1}
初始化结果：
wts =
0 0
bias =
0
dw=learnp(w,p,[],[],[],[],e,[],[],[],[],[])
dw =
1 2
w=w+dw
net.IW{1,1}=w;
a=sim(net,p)
权值学习之后再次仿真预测
结果：
w =
2.0000 1.2000
a =
1
net=train(net,p1,t1)
net =
Neural Network
name: 'Custom Neural Network'
userdata: (your custom info)
dimensions:
numInputs: 1
numLayers: 1
numOutputs: 1
numInputDelays: 0
numLayerDelays: 0
numFeedbackDelays: 0
numWeightElements: 3
sampleTime: 1
connections:
biasConnect: true
inputConnect: true
layerConnect: false
outputConnect: true
subobjects:
input: Equivalent to inputs{1}
output: Equivalent to outputs{1}
inputs: {1x1 cell array of 1 input}
layers: {1x1 cell array of 1 layer}
outputs: {1x1 cell array of 1 output}
biases: {1x1 cell array of 1 bias}
inputWeights: {1x1 cell array of 1 weight}
layerWeights: {1x1 cell array of 0 weights}
functions:
adaptFcn: 'adaptwb'
adaptParam: (none)
derivFcn: 'defaultderiv'
divideFcn: (none)
divideParam: (none)
divideMode: 'sample'
initFcn: 'initlay'
performFcn: 'mae'
performParam: .regularization, .normalization
plotFcns: {'plotperform', plottrainstate}
plotParams: {1x2 cell array of 2 params}
trainFcn: 'trainc'
trainParam: .showWindow, .showCommandLine, .show, .epochs,
.time, .goal, .max_fail
weight and bias values:
IW: {1x1 cell} containing 1 input weight matrix
LW: {1x1 cell} containing 0 layer weight matrices
b: {1x1 cell} containing 1 bias vector
methods:
adapt: Learn while in continuous use
configure: Configure inputs & outputs
gensim: Generate Simulink model
init: Initialize weights & biases
perform: Calculate performance
sim: Evaluate network outputs given inputs
train: Train network with examples
view: View diagram
unconfigure: Unconfigure inputs & outputs
P=[-0.5 1 0.5 -0.1;-0.5 1 -0.5 1];
T=[1 1 0 1]
net=adapt(net,P,T);
因为输入的P、T是数组，因此此处为并行输入，即这里是批量梯度下降的批训练
net =
Neural Network
name: 'Custom Neural Network'
userdata: (your custom info)
dimensions:
numInputs: 1
numLayers: 1
numOutputs: 1
numInputDelays: 0
numLayerDelays: 0
numFeedbackDelays: 0
numWeightElements: 3
sampleTime: 1
connections:
biasConnect: true
inputConnect: true
layerConnect: false
outputConnect: true
subobjects:
input: Equivalent to inputs{1}
output: Equivalent to outputs{1}
inputs: {1x1 cell array of 1 input}
layers: {1x1 cell array of 1 layer}
outputs: {1x1 cell array of 1 output}
biases: {1x1 cell array of 1 bias}
inputWeights: {1x1 cell array of 1 weight}
layerWeights: {1x1 cell array of 0 weights}
functions:
adaptFcn: 'adaptwb'
adaptParam: (none)
derivFcn: 'defaultderiv'
divideFcn: (none)
divideParam: (none)
divideMode: 'sample'
initFcn: 'initlay'
performFcn: 'mae'
performParam: .regularization, .normalization
plotFcns: {'plotperform', plottrainstate}
plotParams: {1x2 cell array of 2 params}
trainFcn: 'trainc'
trainParam: .showWindow, .showCommandLine, .show, .epochs,
.time, .goal, .max_fail
weight and bias values:
IW: {1x1 cell} containing 1 input weight matrix
LW: {1x1 cell} containing 0 layer weight matrices
b: {1x1 cell} containing 1 bias vector
methods:
adapt: Learn while in continuous use
configure: Configure inputs & outputs
gensim: Generate Simulink model
init: Initialize weights & biases
perform: Calculate performance
sim: Evaluate network outputs given inputs
train: Train network with examples
view: View diagram
unconfigure: Unconfigure inputs & outputs
用标准化感知器学习规则（标准化学习数learnpn）进行分类，非标准化感知器学习规则训练奇异样本的结果：
第一部分图形化的结构，这里是2输入，1输出，中间1个隐藏层，有一个节点
第二部分显示的是训练算法，这里是trainc - 循环顺序权重/阈值的训练；误差指标为mae
第三部分显示训练进度：
Epoch：训练次数；在其右边显示的是最大的训练次数，可以设定，上面例子中设为30；而进度条中显示的是实际训练的次数，上面例子中实际训练次数为30次。
Time：训练时间，也就是本次训练中，使用的时间
Performance：性能指标；本例子中为平均绝对误差(mae)的最大值。精度条中显示的是当前的平均绝对误差；进度条右边显示的是设定的平均绝对误差(如果当前的平均绝对误差小于设定值，则停止训练)，这个指标可以用.trainParam.goal参数设定。
Gradiengt：梯度；进度条中显示的当前的梯度值，其右边显示的是设定的梯度值。如果当前的梯度值达到了设定值，则停止训练。
Mu: trainParam这个结构体的参数，确定学习根据牛顿法还是梯度法
validation check为泛化能力检查（若连续6次训练误差不降反升，则强行结束训练）
第四部分为作图。分别点击2个按钮能看到误差变化曲线，分别用于绘制当前神经网络的性能图，训练状态。
性能图：
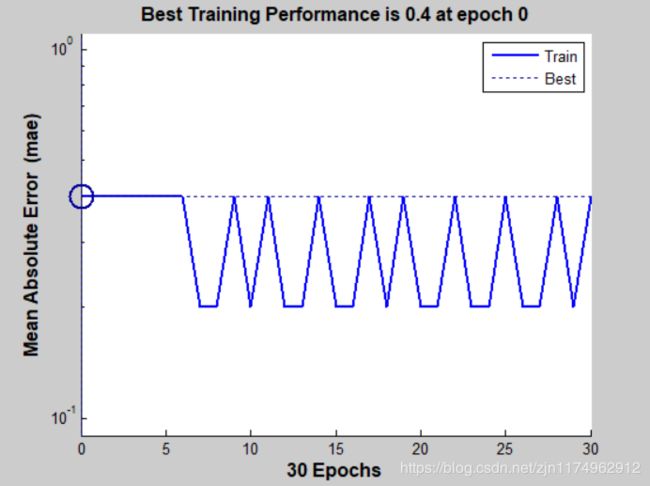
样本分类图：
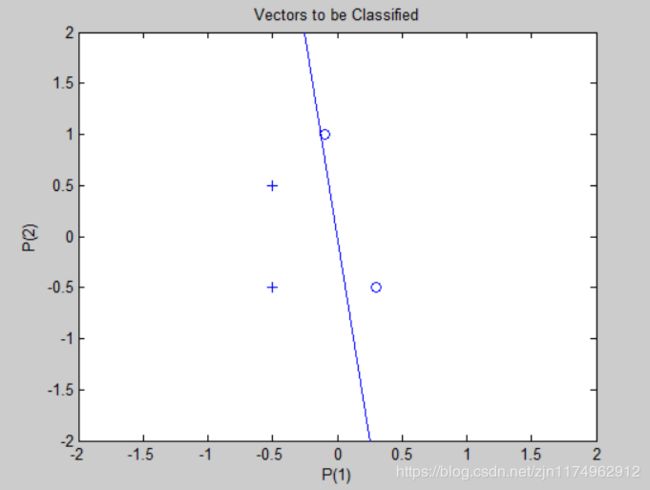设计多个感知器神经元解决分类问题，样本分类图：
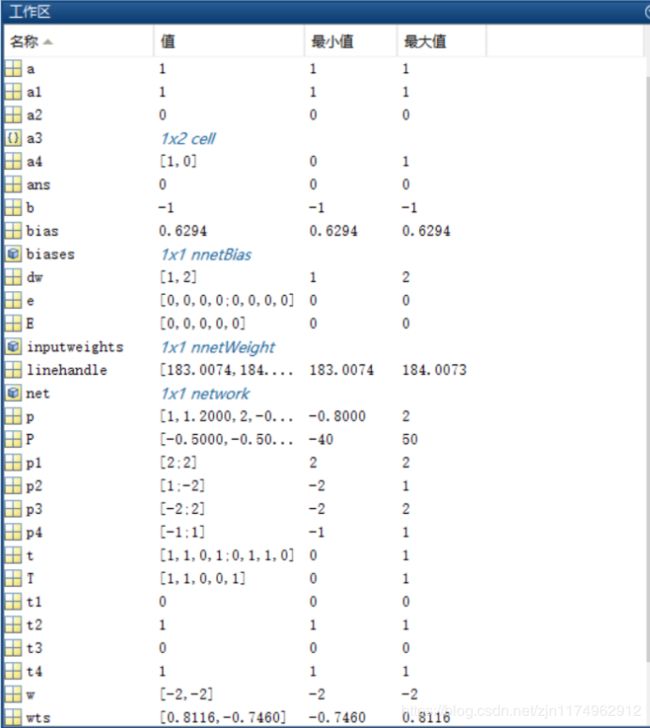
运行完成之后的工作区：
4.小结
感知机算法是一个简单易懂的算法，自己编程实现也不太难。前面提到它是很多算法的鼻祖，比如支持向量机算法，神经网络与深度学习。因此虽然它现在已经不是一个在实践中广泛运用的算法，还是值得好好的去研究一下。