专题：深度神经网络基本问题的原理详细分析和推导

写在最前面

---

• 本文是一篇关于神经网络算法设计的几个基本问题的理论分析的专题文章，涉及到比较多的原理推导。

• 文章的主体理论知识、涉及到的图片资源，大多来自以下几篇教材或者教程：

  • Ian Goodfellow 的《Deep Learning》；
  • Andrew Ng在Coursera的《Machine Learning》课程；
  • 周志华老师的《机器学习》
  • Michael Nielson 的线上书籍：
    http://neuralnetworksanddeeplearning.com/index.html
  • 《随机数学基础》 曹振华 编

• 本文涉及到的概念和理论，尽可能参考自维基百科和原论文的定义和分析并添加自己的理解。尽可能保证所有观点的严密和权威性。做一篇有态度的严谨的技术博文。

• 在一些细节问题上，参考来自Quera、知乎、CSDN等网络帖子的综合分析推敲而成，我会在每个章节的末尾对引用进行统一说明。

• 文章内容较长，主体分为以下几个部分，大家可以根据自己的需要选择对应的章节阅读：

  • 首先，我们会大概描绘神经网络的整个执行过程，让大家对神经网络有基本的认知，并说明这个过程会涉及到的几个方面的问题；

  • 接着，按照神经网络执行过程展开，我们将从全局到细节的角度来逐步解决神经网络执行过程中我们会遇到的问题：

    • 首先，前馈传播过程中，神经网络是如何拟合一个函数的，我们将用直观的方法解释神经网络如何构造模型，逼近一个函数的，以此解释神经网络的基本性质：通用逼近性质(Universal Approximation Properties)，之后，简单说明神经网络的单元数，层次的关系；

    • 接着，将介绍我们如何进行目标优化：也就是如何优化我们前面构造的这个逼近原函数的模型，让他和真实的模型尽可能接近。这里主要讲解梯度的下降方法，提及非梯度的下降方法，具体而言，我们会主要介绍梯度下降法。；

    • 知道目标的优化方法之后，我们接着会以基于梯度的学习方法为优化方法，介绍与其相关的两个问题：如何选取优化目标和如何得到优化目标的梯度：

      • 为了解决如何选取优化目标的问题，我们会介绍两个方面的内容：

        • 优化目标的形式确定：关于极大似然法，交叉熵代价函数的理论分析推导；

        • 如何作为优化目标中所需要使用的概率分布模型，并得到对应的输出单元的激活函数，这里会涉及到：

          • 使用广义线性模型和指数族的原理构造我们常见的输出单元函数并说明其和概率分布模型的对应关系；
          • 如何解决sigmoid等输出单元的饱和问题；

      • 为了解决如何得到优化目标的梯度的问题，我们将介绍**反向传播算法(BP算法)**进行逐步推导

    • 最后，我们将结合前面所述的算法和原理的特点，介绍隐藏层的激活函数应该具有怎样的性质，并对常见的激活函数的特点进行简要的分析；

当然，作者水平有限，难免会有很多疏忽的地方，欢迎各位多加指正！

1 神经网络算法的直观了解

本章节，我会从比较宏观的角度和大家一起回顾一下神经网络算法涉及到的比较重要的问题，并且用这些概念对神经网络的运算过程做一个简要的说明。这里涉及到的概念和问题，都会在之后的章节进行具体阐述。

1.1 神经网络过程描述：

首先，要明确，神经网络做的是预测任务，相信你记得高中学过的最小二乘法，我们可以以此做一个不严谨但比较直观的类比：

• 首先，我们要得到一个数据集和数据集的标记（最小二乘法中，我们也得到了一组组x,y的值）
• 算法根据这个数据集和对应的标记，拟合一个能够表达这个数据集的函数参数（也就是最小二乘法中计算$a$, $b$的公式，神经网络中不过是这个公式没法直接得到）
• 我们以此得到了拟合的函数（也就是最小二乘法中的拟合直线$\hat{y}=ax+b$）
• 接下来，带入新的数据之后，就可以生成对应的预测值$\hat{y}$（在最小二乘法中，就是带入$\hat{y}=ax+b$得到我们预测的$\hat{y}$，神经网络算法也是的，只不过求得的函数比最小二乘法复杂得多）。

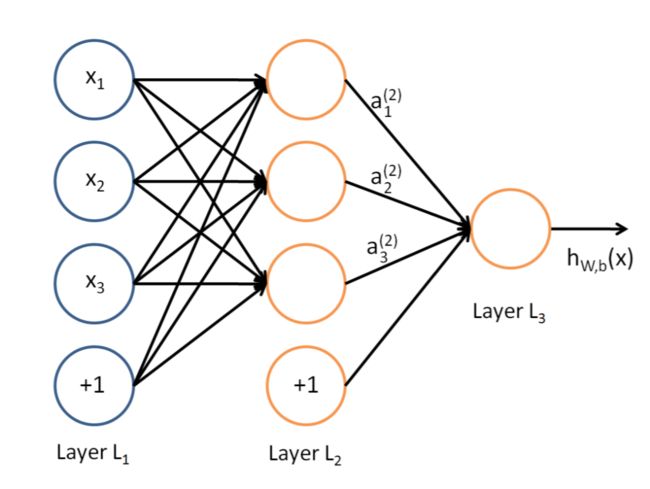
下面我们稍微具体一点描述一下神经网络算法完成任务的过程，下面是一张典型的神经网络(浅层神经网络)的示意图：

我们把任务分成建模和训练两个过程来看：

• 首先是建立模型：

  • 网络结构：包括每一层的结构和层级间的连接结构

    • $L_1$是输入层(Input Layer)，直接获取输入的数据，其中每个unit一个特征。$x_1,x_2,x_3$是一个用于训练的一个样本的三个特征。如果我们现在要完成手写体识别的任务，那么每一个$x_i$就是我们输入的图片样本的每一个像素。“+1”是偏置单元

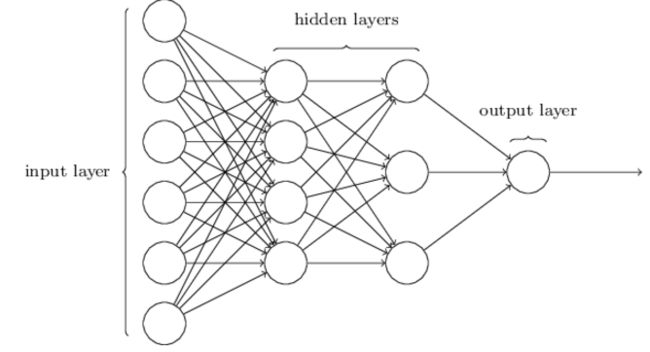
    • $L_2$是隐藏层(Hidden Layer)，每个Unit收集来自上一层的全部特征进行线性组合后，作为输入，带入我们的激活函数$h_{\theta }(z)$中，得到一个输出值$a_i^{(j)}$，其中,$J$代表参数所属层次，$i$代表了该神经元在$j$层的具体位置。在深层神经网络中，隐藏层可以有多个。并且，每个隐藏层会以前一个隐藏层的输出为函数的输入，带入本层的激活函数中，下面的图，就是一个多隐藏层的例子：
      

    • $L_3$是输出层(Output Layer)，他的一个单元所做的工作和隐藏层很相似，把上一层的输出进行线性组合后，作为输入，带入输出层的激活函数单元，便可以得到这个神经元的输出。我们上面的图中对应的都只有1个输出单元，用于二分类，也就是预测0或者1；我们也可以有多个输出单元，每个输出单元代表一个预测值。（当然，使用某些激活函数，比如softmax，可以让你的一个输出单元就能完成多分类问题），下面，是一个多个输出单元的网络例子：
      

  • 激活函数：
    激活函数的主要作用是表达非线性，并且进行上层的输出线性组合后的值域，到本层的输出的值域的压缩

    • 从隐藏层一直将数据传递到输出层，也就得到了我们的分类结果，在原图中，我们的输出层只有一个单元，对其建立的一个二分类的模型，根据决策边界，做出最后分类的决策判定，在二分类问题中，决策就是YES or NO。（决策边界后文不会提及，但是很好理解，就是分类为正类和反类的边界，通常在sigmoid这种值域为(0,1)的函数，我们的决策边界是0.5，当我们对查准率（不判错的概率）和查全率（不漏判的概率）有额外的需求的时候，会对这个参数做出调整）

• 计算模型对于数据集的最优参数（基于梯度的优化为例），过程大体可以分成几个步骤：

  • 首先，使用前馈传播(Feedforward Networks)方法来将输入数据代入网络，一层层地“送到”输出层，得到本次的样本数据的“预测估计值”，比如房屋的价格可能是多少，比如这个西瓜是好瓜还是坏瓜；

  • 得到预测估计值之后，带入代价函数，使用反向传播算法，得到每一个网络网络单元的误差值(实际上是梯度值)；

  • 使用基于梯度的优化算法，首先根据代价函数计算模型的每一个参数的梯度，根据根据梯度计算“惩罚值”，调整模型参数，让他向优化目标接近。

  • 通过上述迭代，直到得到符合要求的优化目标；

    • 最后，用户只要输入一个数据，就会经过前馈传播网络，得到一个比较理想的分类结果

1.2 神经网络相关的几个问题

1.2.1 表征假设和激活函数

• 神经网络是由一个个神经元链接而成的整个模型。每个神经元有一个激活函数(Activation function),能够将输入数据压缩到指定区间，并且让原本线性的特征组合通过激活函数表现出非线性的特征。
• 我们需要考虑的是用什么样的激活函数能够满足这种要求，每个激活函数各有什么特点，哪种最适合我们面临的问题。

1.2.2 结构设计(Architecture Design)

• 比起Logistic Regression 等其他的机器学习算法，神经网络，增加了多层次的网络概念，所以我们还需要解决的问题就是神经网络的结构的问题，比如层次深度和单层的神经元个数如何权衡。
• 我们还需要设计神经单元的链接形式，在一些神经网络算法中，比如递归神经网络，卷积神经网络，不是简单的全链接

1.2.3 代价函数(Cost Function)和优化目标(Optimization objective)

• 我们用代价函数来描述当前预测模型的效果和经验分布（empirical distribution）相比较的准确程度，也就是模型预测的准确程度。根据准确程度，我们给当前的模型的参数给予对应的“惩罚”。我们的目标是，让我们离优化目标越来越接近。

• 在神经网络中，利用极大似然估计（Maximum Likelihood Estimation）和交叉熵（cross-entrogy）来产生代价函数。同时，以此为基础确立了我们的优化目标。

• 优化目标一般是代价函数的最大值和最小值，但有时候我们会在建立代价函数的基础上加上其他参数(比如正则项)作为我们的优化目标函数。

1.2.4 如何进行优化

• 知道了优化目标之后，我们需要让我们的模型逐渐靠近我们的优化目标，梯度下降法是一种比较常见的优化方案，此外还有牛顿下降法等。这个优化过程也就是所谓的模型的学习过程
• 在神经网络中，我们使用基于梯度下降的学习方式，在这个过程中，我们需要解决的问题就是：用于进行调整的每一个单元的偏导项$\frac{\partial J(\Theta )}{\partial \Theta }$ 要如何进行计算。这就是大名鼎鼎的反向传播算法所要完成的任务。

1.3 参考资料

• “CHAPTER 1Using neural nets to recognize handwritten digits” by Michael Nielsen
• 《Machine Learning》 in coursera by Andrew Ng

2 前馈传播和结构设计

首先，神经网络是如何拟合一个函数的，我们将用直观的方法解释神经网络如何逼近一个函数的，以此解释神经网络的基本性质：通用逼近性质(Universal Approximation Properties)，简单说明神经网络的单元数，层次的关系。

2.1 通用逼近性质(理论)(Universal Approximation Properties(Theorem))：神经网络可以逼近任意函数

2.1.1 本章节说明

• 通用逼近性质是我自己的翻译，不一定权威。

• 通用逼近性质（Universal Approximation Properties）是神经网络中非常重要的一个性质，虽然这不会在直接用于构造一个神经网络，但是他告诉我们：一个仅有单隐藏层的神经网络。在神经元个数足够多的情况下，通过非线性的激活函数，足以拟合任意函数。这使得我们在思考神经网络的问题的时候，不需要考虑：我的函数是否能够用神经网络拟合，因为他永远可以做到——只需要考虑如何用神经网络做到更好的拟合。

• 这个算法的证明需要用到很多数学知识（包括：Hahn-Banach 理论, Riesz Representation 理论, Fourier analysis），所以实际上他不容易理解。本文也不采用直接的数学证明的方式来证明这个定理，因为对于更多情况下，我们只需要直观理解足够了，为了方便有兴趣的读者阅读严谨的数学证明，以下是原论文链接：
  http://www.dartmouth.edu/~gvc/Cybenko_MCSS.pdf

• 另外Michael Nielson的教程中，使用另一种方式，也提供了可视化的证明过程：
  http://neuralnetworksanddeeplearning.com/chap4.html。
  网站使用了一些js脚本，使得我们可以直接操作整个神经元的优化过程，非常有趣

• 我们不会直接证明神经网络的通用逼近性质，只是向大家展示神经网络的每一个迭代过程，便于大家有直观的理解。

2.1.2 通用逼近定理的严谨表述

2.1.2.1 来自“Approximation by Superpositions of a Sigmoidal Function”这篇论文的观点

• 这篇文章的原文摘要：
  In this paper we demonstrate that finite linear combinations of compositions of a fixed, univariate function and a set of affine functionals can uniformly approximate any continuous function of n real variables with support in the unit hypercube; only mild conditions are imposed on the univariate function. Our results settle an open question about representability in the class of single bidden layer neural networks. In particular, we show that arbitrary decision regions can be arbitrarily well approximated by continuous feedforward neural networks with only a single internal, hidden layer and any continuous sigmoidal nonlinearity. The paper discusses approximation properties of other possible types of nonlinearities that might be implemented by artificial neural network
  原文链接：http://www.dartmouth.edu/~gvc/Cybenko_MCSS.pdf
• 说明：文章证明在只有单个隐层的情况下，对于任何的连续的，非线性的sigmoidal函数，只要在隐藏层网络单元足够多的情况下，就能够很好的拟合任意的连续函数。
• 文中关于sigmoidal函数的定义如下，如果$\sigma$是sigmoid函数，那么：
  \begin{eqnarray}
  \sigma(t)=
  \begin{cases}
  1 & x\rightarrow +\infty \
  0 & x\rightarrow -\infty \
  \end{cases}
  \end{eqnarray}
• 文中关于sigmoid函数的线性组合的定义如下，如果$G(X)$是$\sigma$的线性组合，则：
  $$G(x)=\sum _{j=1}^N{\alpha }_j\sigma (y_j^{T}x+b_j)$$
  其中$x$是输入的变量，他可能是一个$x\to R^n$的向量。
• 因此，通用逼近性质公式化的表述为，对于任意的函数$f(x)$，存在$G(x)$，使得对任意$ϵ>0$，有，下式成立：
  $$|f(x)-g(x)|<ϵ$$
• 细心的读者可以看到，这里使用的sigmoidal性质的函数和我们的sigmoid的函数略有差异(值域不一样)，但实际上只是其经过缩放加平移而成而已。

2.1.2.1 来自“On the Number of Linear Regions of Deep Neural Networks”这篇论文的观点

• 看到关于Universal approximation theorem的表述，我想一定有读者产生和我一样的疑问：我们常用的ReLU激活函数并不符合上述定理证明时的sigmoidal限制，他只是一个分段线性的函数(若此时您还不知道ReLU是什么，可以翻阅文章最后一章“激活函数”)。那么，他还具有这个性质么?
• 带着这个问题，我查阅了一些文献，在Eric Jang于Quera的回答中查到了我认为比较合理解释：
  就如我们所猜想的那样，ReLU仅仅是分段线性函数，并不是一个非线性的函数，所以实际上，他得以拟合函数的原理其实并不像sigmoidal类的函数，是作为一个函数逼近器。其实上，他只是通过ReLU在$f(0)=0$的函数性质的突变(由恒等函数到突然消失，恒为0)，来取得一个将一个函数分段的效果。实际上，如果我们仅仅使用ReLU来进行拟合，最后得到的是一个极其复杂的分段函数，所以实际上，比起函数逼近器，他更适合被称作函数分割器。在下面章节中，我会具体用例子阐述这个过程。
• 原回答链接：
  https://www.quora.com/How-can-a-deep-neural-network-with-ReLU-activations-in-its-hidden-layers-approximate-any-function/answer/Eric-Jang?srid=6Y6o
• 原论文地址：
  https://papers.nips.cc/paper/5422-on-the-number-of-linear-regions-of-deep-neural-networks.pdf

2.1.2 从非线性讲起：为什么使用激活函数：

首先我们看这个简单的神经元

$a_1$，$a_2$作为输入，通过$b_1$进行输出，假设我们$b_1$使用的是恒等函数（即$f(z)=z$）作为激活函数，则这是一个线性模型。因为
$$f(z)=f(w_1{a}_1+w_2{a}_2)=w_1{a}_1+w_2{a}_2$$
其中，$w_i$是连接$a_i$和$b_1$的权重。
现在我们使用恒等模型来构造一个单隐层的神经网络，为了方便表述，我们没使用全连接的网络，并且没有表述偏置单元，但是也足以表达我们想要说明的问题：

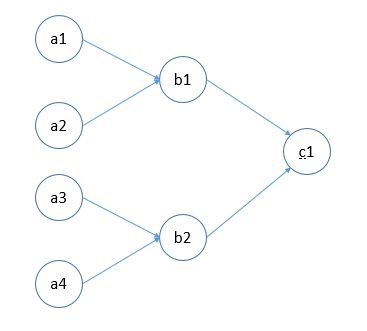
则我们的到的$c_1$的输出的表达式为：
KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ c_1&=f(W_{21}b…
其中，$W_{ij}$是连接接第$i$层和第$i+1$层的第$j$个单元的权重。
可以看到，我们的结果仍然是做一个线性组合，不论我们使用多少隐藏层，每层多少个单元，都是这个结果。这就道出了我们所说的激活函数的存在意义：他希望能够增加模型的非线性性，以拟合复杂的函数，下一节会具体表述这个问题。这也是我们选择一个激活函数必须满足的标准之一。

2.1.3 前馈网络拟合函数过程：

• 还是上面这张图
  
  和对应的公式
  KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ c_1&=f(W_{21}b…
  如果我们的激活函数使用的不是线性函数，我们直观想象一下，神经网络做了什么（前面为了简化公式把$b$去掉了，这里我们把偏置单元$b$加上）：
  $$f(W^{T}X+b))$$
  首先，我们使用$W^{T}X+b$对该单元之前的单元得到的$X$进行线性组合。之后，经过激活函数得到一个非线性函数。通过线性组合的$W$和$b$的不同取值，我们可以得到该非线性激活函数的任意不同表达形式（有的被拉长，有的被平移）;

• 假设我们能拿到非常多个该非线性函数的不同表现形式，在输出层中，对这些函数进行再次线性组合$W^{T}f(z)+b$，拿到新的组合后的函数，我们可以表达出一个更复杂的函数，通过不同参数的值的选择，可以使得我们生成的函数和真实的函数差距越来越小，这就是拟合的过程。因此，可以直观上认为，这可得到任意的函数，这就是神经网络的Universal Approximation Properties的直观理解。

• 而深度神经网络，做的就是这个反复的线性变换组合，非线性激活函数压缩；可以想象，通过重复这个过程，我们能够得到越来越复杂的函数的线性组合，一直到我们最后输出层的拟合函数。而之后提到的BP算法，就是希望我们得到的线性组合的函数和实际函数的偏差尽可能小。我们接下来以ReLU为例，来具体说明这个过程。

2.2 前馈网络进行逼近的拟合过程

有一个非常好用的即时反馈神经网络训练模型结果的网站：
http://cs.stanford.edu/people/karpathy/convnetjs/demo/regression.html

2.1.1 以sigmoid为例

我们将利用这个网站进行讲解，首先，我们使用下面的代码来输出化网络：

layer_defs = [];
layer_defs.push({type:'input', out_sx:1, out_sy:1, out_depth:1});
layer_defs.push({type:'fc', num_neurons:4, activation:'sigmoid'});
layer_defs.push({type:'regression', num_neurons:1});

net = new convnetjs.Net();
net.makeLayers(layer_defs);

trainer = new convnetjs.SGDTrainer(net, {learning_rate:0.01, momentum:0.0, batch_size:1, l2_decay:0.001});

我们构造了一个单隐含层，这个隐含层有4个sigmoid为激活函数的神经元组成。

• 现在，我们构造了一个隐藏层具有4个神经元的神经网络，并且使用ReLU作为激活函数。首先大家看下面这幅图，4条红色的线，就是4个隐藏层单元的输入和Input层的输入的函数关系，这是经过线性变换得到的，也就是$WX+b$：
  

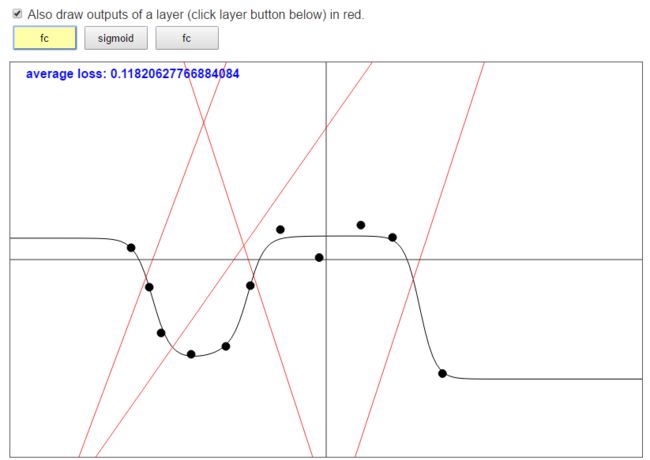
• 接下来，我们做的事情就是把这4个进行线性变换之后的函数带入激活函数$g(z)=\frac{1}{1+e^{-z}}$，得到下面的这4个函数图像：
  
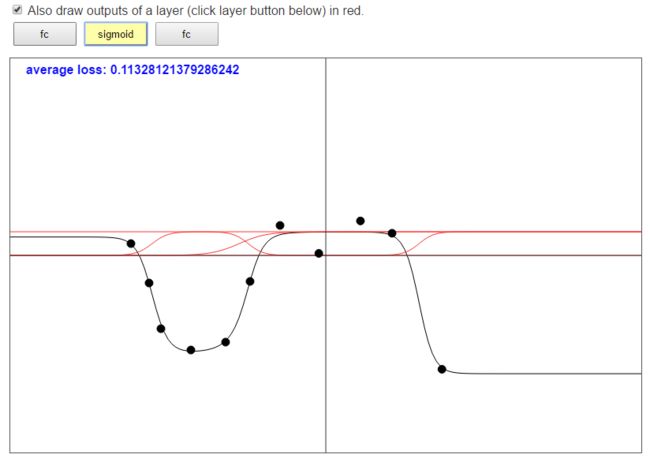
  大家可以看到，第一张图中输出为0的点，就是第二张图中输出为0.5的点。

• 接下来，我们得到了这4个函数之后，再分别进行线性变换$WX+b$，还是这个公式，但是现在$X$是我们从上一层$g(z)$中得到的输出，这一步，我们会将得到的4个函数通过线性组合变成一个函数：
  

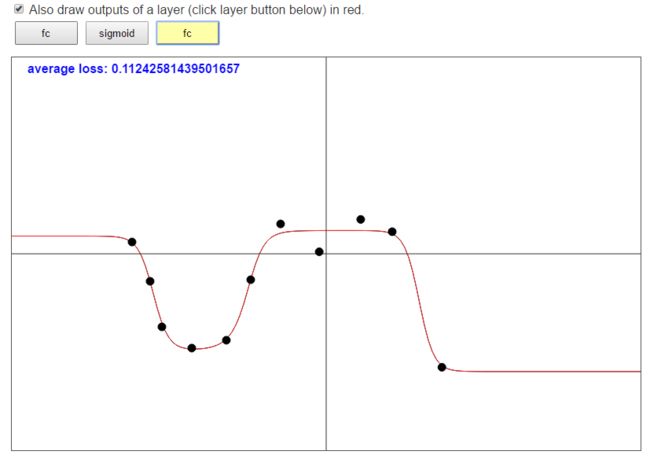
• 这个函数也就是我们最终输出的拟合函数，当我们的神经元个数越多，我们就有足够多的函数的选择，我们再将选择好的函数进行组合，通过调节参数的值，便可以达到我们想到的效果；

2.1.1 ReLU的拟合

• 现在，我们构造了一个隐藏层具有三个神经元的神经网络，并且使用ReLU作为激活函数。首先大家看下面这幅图，三条红色的线，就是三个隐藏层单元的输入函数，也就是之前的$WX+b$。
  

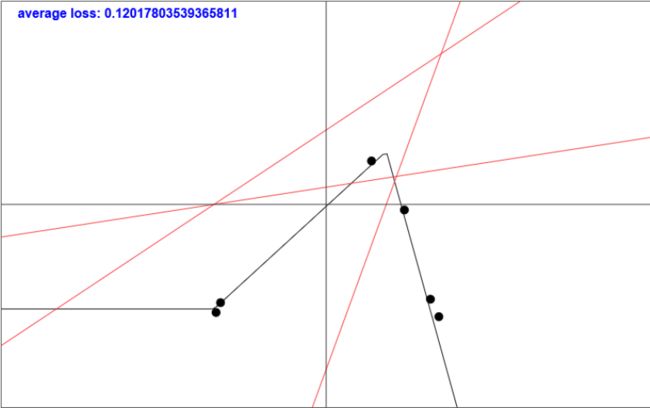
• 接下来，我们做的事情就是把这三个进行线性变换之后的函数带入激活函数$g(z)=max(0,z)$，得到下面的这三个函数图像：
  
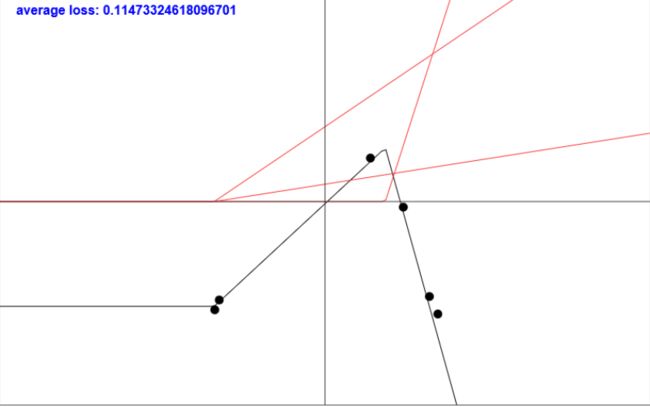
  可以看到，ReLU做的事情就是折叠x轴以下的部分，保留X轴以上的部分

• 接下来，我们得到了这三个函数之后，再分别进行线性变换$WX+b$，还是这个公式，但是现在$X$是我们从上一层$g(z)$中得到的输出，这一步，我们会将得到的三个函数通过线性组合变成一个函数：
  

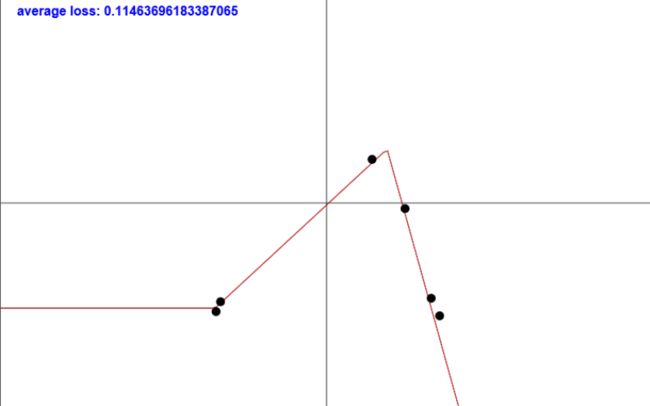
• 这个函数也就是我们最终输出的拟合函数，我们仔细分析一下这个变换过程：
  
  可以看到，我们最后你拟合的直线大概是由a-b+c组成的。也就是说，通过ReLU，我们能够得到的不是一个严格的曲线，而是一个分段线性的函数。大家再仔细看这三只ReLU的分段点（也就是由恒为0到变成恒等函数的地方），与其对应的就是我们最终拟合分段线性函数的分段点。。

• 当我们的神经元个数越多，这个分段就能够被分得越细，可以想象，当我们拥有无穷多个整流单元进行线性组合，可以表达出任意我们想要的非线性函数。所以说，ReLU与其说是一个在做一个逼近，不如说是在做一个分段。

2.3 关于通用逼近定理的补充说明

• 再次强调：通用逼近定理只告诉我们一个仅有单隐藏层的神经网络,在神经元个数足够多的情况下，通过具有sigmoid性质(非线性的、压缩的)的激活函数，足以拟合任意函数。是神经网络中非常重要的一个证明，虽然这不会在直接用于构造一个神经网络，但这使得我们在思考神经网络的问题的时候，不需要考虑：我的函数是否能够用神经网络拟合，因为他永远可以做到——只需要考虑如何用神经网络做到更好的拟合
• 即使如此，我们至少面临以下的几个问题：
  • 我们的优化方法不一定能够找到我们所希望的优化参数，也就找不到我们需要的拟合函数。尽管我们知道这个拟合函数是存在的
  • 在优化过程中，我们可能使用不对的参数，结果便是获得了错误拟合函数，这个拟合函数能够很好的拟合我们的输入数据，却没有泛化能力（预测输出能力），这便是过拟合问题
• 经验告诉我们：
  • 使用更深层的神经网络，可以得到更好的表达效果，直观的理解是：在每一个网络层中，函数特点被一步步的抽象出来；下一层网络直接使用上一层抽象的特征进行进一步的线性组合。而使用浅层网络中，你需要使用更多的神经元才能有办法表达出相应的特征。
  • 然而，深层神经网络带来的另一个问题就是：他的优化比较困难

2.4 参考资料

• ConvnetJS demo: toy 1d regression
• 《Deep Learning 》by lan Goodfellow in “6.4 Architecture Design”
• Universal Approximation Bounds for Superpositions of a Sigmoidal Function
• Answer of “How can a deep neural network with ReLU activations in its hidden layers approximate any function?” in Quera write by Eric Jang
• on the number of linear regions of deep neural networks
• “Chapter 4:A visual proof that neural nets can compute any function” by Michael Nielsen

3 目标优化

接着，将介绍我们如何进行目标优化：也就是如何优化我们前面构造的这个逼近原函数的模型，让他和真实的模型尽可能接近。这里会涉及到基于梯度的下降方法，基于非梯度的下降方法，具体而言，我们会主要介绍梯度下降法。

• 目标优化所做的任务是最小化或者最大化某个函数$f(z)$，需要注意的是，我们一般使用的是最小化某个函数，最大化的问题也可以转化为最小化$-f(z)$的问题；
• 这里的$f(z)$有很多种叫法：目标函数(objective function)或者标准(criterion)，我们也叫他代价函数(cost function or loss function)。当然有些作者会给代价函数赋予其他特别的意义。
• 我们还没有具体介绍代价函数，所以这里提前强调一下，这个$f(z)$不是我们求得的模型的表达式，而是表达我们得到的拟合函数和真实的函数的差距大小的概念。
• 一般，我们使用$\ast$来表达某个函数的最大值或者最小值的概念，比如：
  $$x^{\ast }=arg\min f(x)$$

3.1 基于梯度的目标优化

3.1.1 从单变量函数开始

假设$y=f(x)$,$x$和$y$是实数，我们用$f^{{}^{\prime }}(x)$或$\frac{\partial y}{\partial x}$表达他的一阶导函数(derivative)。他代表的是曲线在$x$点的斜率(slope)。所以说，如果说有一个比较小的$ϵ$作为自变量的变化范围，可以得到
$$f(x+ϵ)\approx f(x)+ϵf^{{}^{\prime }}(x)$$
因此，导数能够表达在一个小范围的自变量$x$的改变中，输出的$y$的变化快慢程度。我们可以以此来求得函数的极值：比如当我们求的是局部最小值时，我们已知：
$$f(x-ϵsign(f^{{}^{\prime }}(x)))<f(x)$$
其中sign(x)是一个代表方向的函数，如果x>0，sign(x)=1，如果x<0,sign(x)=-1，如果x=0，sign(x)=0。
那么，我们可以推测，我们只要向梯度的相反方向增加一小步(a small step)，我们可以使得$f(x)$的值更小一点，具体可以看下面这张图：

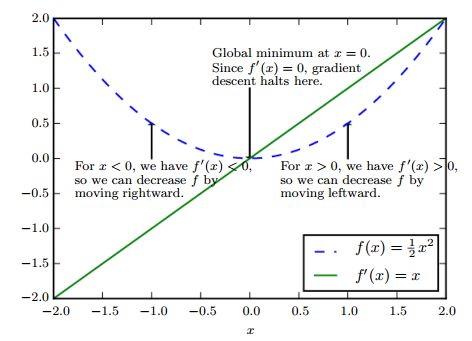
反复迭代这个过程，我们就可以不断走到$f^{{}^{\prime }}(x)=0$的点，我们把他叫做临界点(critical points)或者固定点(stationary points)。临界点可能有三种情况，如下图所示：

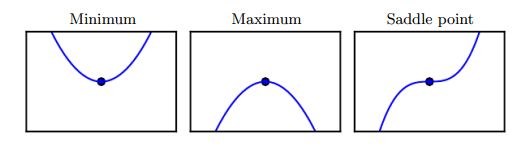
他可能是局部最小点(local minimun)，局部最大点(maximum)，鞍点(saddle point)。很直观，不多解释。
接下来我们要解决的问题就是，局部最小点有很多，我们也可能求导鞍点，这些都不是我们要想要的全局最小值(global minimum)。我们的解决方案是：做一个折中，我们只要求求得的$f$非常小，只要足够小，我们就停止梯度下降，而不是非要达到梯度全局最小值。具体情况如下图所示：

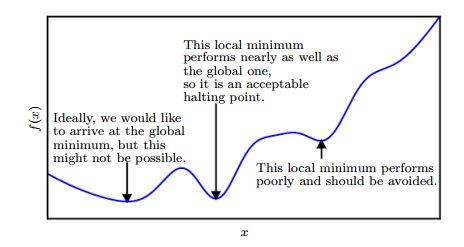
这里要重新强调一下，我们这里的$f$并不是拟合的函数本身，而代表的是我们拟合的函数和真实函数的差距，他一般是一个大于等于0的数，所以我们可以通过这个数据的要求大小来达到规定拟合函数的准确程度，比如0.01，当模型的的准确程度达到我们的要求之后，参数拟合便完成了。
到这里，就是梯度下降法的全部思想了，接下来的一节，我们将把这个理念应用到多元函数中。

3.1.2 多元函数的梯度下降

• 现在，我们重新开始假设，将$f$变成一个$R^n\to R$的函数，他的输出仍然是一个标量，但是输入则是一个多元的变量。因此，我们需要使用到偏导数（partial derivatives）的概念。在偏导数中$\frac{\partial f(x)}{x_i}$意味着在$x$点中$x_i$方向的增量。
  因此，我们对梯度的概念也要对应做出调整：梯度是一个向量，这个向量的维度和$x$的维度一样，每一个维度对应着$f(x)$在$x_i$这个方向的偏导数。我们用${▽}_{x}f(x)$来表示整个梯度。临界点(critical points)的概念也对应调整为：梯度的每一个元素都是0的点$x$

• 另外，因为我们的函数，梯度都是有多维的，所以我们选择"走一小步"也就多了"往哪个方向"走的问题需要解决，我们的目标是，寻找梯度下降最快的地方（在前面的问题中，我们直接选择梯度符号的反方向即可）。为此，我们要提出方向导数(directional derivative)的概念：$u$是一个方向导数，意味着它是$f$在$u$上的斜率。更规范的表达式，他是$f(x+\alpha u)$在$\alpha =0$时对$\alpha$的求导，使用链式法则，我们可以得到：
  $$\frac{\partial f(x+\alpha u)}{\partial \alpha }=u^T{▽}_{x}f(x)，当\alpha =0$$那么，为了达到最小的$f$， 我们需要找到下降最快的方向，作为我们梯度下降的方向，也就是说，我们需要找到一个方向导数，满足：
  KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ u^*&=\min_{u,u…
  其中，$u^{T}u=1$意味着这是一个模为1的方向向量。这个式子的推导用的是向量内积公式
  $$x\cdot y=||x|{|}_2||y|{|}_2\cos \theta$$
  其中$\theta$是两个向量的夹角，$||x|{|}_2$是向量$x$的模。
  因为$u$是单位方向向量，所以$||u|{|}_2=1$，而$||{▽}_{x}f(x)||$的大小由$x$决定，与方向向量$u$无关，所以要求$u$，要考虑的仅仅是$\cos \theta$，也就是：
  $$u^{\ast }=\underset{u}{\min }\cos \theta$$
  所以我们的问题简化成，寻找$\cos \theta$最小时的$u$的方向，就是我们梯度变化的方向，而$\theta$代表的是$u$和梯度${▽}_{x}f(x)$的夹角，这个问题很容易得到答案了：当$u$和梯度${▽}_{x}f(x)$夹角为180°，也就是方向相反时，$\cos \theta =-1$为最小值，此时的方向导数为梯度下降速度最快的方向,至此，我们成功得到了梯度下降(method of steepest descent or gradient descent)的最终公式了：
  $$x^{{}^{\prime }}=x-ϵ{▽}_{x}f(x)$$
  其中$ϵ$是学习率(learning rate)，代表梯度下降的快慢，他的选择也有一些学问，我们将在下一节介绍

3.2 学习率(learning rate)的选择

比较传统的梯度下降法的学习率是一个常数；很多后来改进的算法则有使用动态学习率的方法出现。本节主要介绍常数的学习率应该如何选择；并对其他方法进行一个简要讲解

首先，有一个重要的性质：我们的优化目标应该随着每次的迭代更新而逐渐减小。否则，我们的梯度下降法可能处于不正常的状态。

• 如果学习率太小：
  如果学习率太小，很显然，结果将是我们的优化目标下降速度十分的慢，如果遇到这种情况。我们需要调整我们的学习速率。
• 如果学习率太大：
  如果学习速率太大，将可能导致迭代过程直接越过极小点，而到了函数的另一边的情况，如图所示：
  
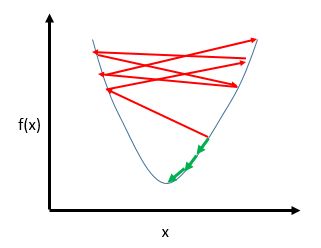
  其中绿色箭头代表的是我们正常情况下，每次迭代都会向f(x)较小的地方靠近，而如果学习率过大，迭代时x可能直接越过中间的极小点，跑到了另一边去，就如图中红色的箭头所表示的一样，因为步长过大，目标函数会在一个比较大的取值范围内上下徘徊，效果如下图所示：
  
  其中红色的线是学习速率过大的情况，绿色的线是正常情况下应该有的曲线。
• 在一些改进算法中，一些算法对学习率进行了动态调整，使得他能够适应不同的梯度情况；

3.3 其他优化算法

关于其他的优化算法，因为不会在接下来的讲解中涉及，所以此处就稍微提一下相关概念，如果以后有时间，再把相关内容完善

• 除了使用迭代的方法进行梯度下降的求解，我们还可以直接计算$ \bigtriangledown _x f(x)=0$来找到局部极小值，避免迭代计算过程，这种方法叫做标准方程法（Normal Equation）
• 除了使用基于梯度的方法之外，我们还可以使用基于一阶导数和二阶导数结合的方法来计算梯度，这个方法典型的就是牛顿法

3.4 参考资料

• 《Deep Learning 》by lan Goodfellow in “4.3 Gradient-Based Optimization”
• 《Machine Learning》
  https://www.coursera.org/learn/machine-learning

4 基于梯度的神经网络优化

上一节我们介绍了优化目标，我们接着会以基于梯度的学习方法为优化方法，介绍与其相关的两个问题：如何选取优化目标和代价函数和如何得到优化目标的梯度。
我们屡次强调，优化目标中的目标函数并不直接是我们的模型的函数，那么，最终我们，如何完成这一个转换?
首先，神经网络使用的是极大似然法的思想，并进一步使用交叉熵作为目标函数的表达式模型，这是我们的第一部分内容；
上一步中，我们会得到一个似然函数的未知函数模型，接着，我们要使用不同的概率分布模型作为代价函数中的似然函数。我们使用的是广义线性模型的思想，最终得到了概率分布模型和激活函数的对应关系。至此，就形成了从函数模型到优化目标的链接，这是我们的第二部分内容
完成了优化目标的表达式之后，我们要解决的最后一个问题是，优化目标的梯度如何获得，这里我们会使用反向传播算法进行实现，这是我们的第三部分内容。

4.1 目标函数的表达式模型的确定

4.1.1 极大似然法和交叉熵（Maximum Likelihood Estimation）

4.1.1.1[概率统计知识]总体，样本，随机变量，独立同分布，参数估计

• 总体(population)：

  • 在数理统计中，我们把研究对象的全体组成的集合称为总体。例如，如果把灯泡作为研究对象，则某工厂生产的所有灯泡就组成了总体。

  • 我们研究的总体，一般不会研究总体的所有指标，我们只对其中一个或者几个指标$X$感兴趣。比如对于灯泡而言，我们只关心他的寿命，对形状不感兴趣。所以，一般我们把总体等同于总体中我们感兴趣的指标$X$的取值的全体，注意的是，$X$一般是随机指标（也就是有多种可能的取值），确定性指标没有统计意义。

  • 个体指的就是$X$的取值。

• 样本（sample）

  • 在随机抽样中，我们对总体进行抽样观测，就得到总体指标$X$的一组具体数值$(x_1,x_2,...,x_n)$，其中每个$x_i$指的是某一个观察的个体的**$X$指标的值**。$(x_1,x_2,...,x_n)$称为容量为$n$的样本的观察值(observation)

  • 在随机抽样中，我们的具体的一次观察的结果$(x_1,x_2,...,x_n)$是确定的数值，但是他随着每次抽样观察而改变。所以我们在泛指可能得到的结果，就不能把$(x_1,x_2,...,x_n)$作为确定的数值，应看成一组随机变量$(X_1,X_2,...,X_n)$，这一组随机变量就是一个容量为$n$的样本；

  • 需要注意的是：在神经网络中，统计学的样本的概念对应的是我们用于训练的数据集；而每一个样本单元才是对应的数据集的单个数据。

• 独立同分布假设(independent and identically distributed (i.i.d.))：

  • 在概率统计理论中，如果变量序列或者其他随机变量有相同的概率分布，并且互相独立，那么这些随机变量是独立同分布。

  • 简单随机采样的每一个样本的随机变量是独立同分布的，意味着一个样本的每个变量相互独立并且分布相同。独立同分布是使用极大似然法的前提条件。

• 参数估计(Parameter Estimation)

  • 希望解决的问题：一般，我们都是已知一个总体$X$的分布，根据分布，得到各个观测值的概率。而参数估计相反。首先，通过具体问题的实际背景，或者其他方面的知识，确定总体$X$的分布形式，但是我们不知道分布中的未知参数的具体值。那么，如何根据样本信息来确定未知参数，这就是参数估计问题。简单说，是一种已知模型，估计参数的方法。

  • 参数估计的标准提法：

    • 假设总体$X$的分布为$f(x;\theta )$（若$X$是连续型随机变量，$f(x;\theta )$为$X$的概率密度，若$X$是离散型随机变量，$f(x;\theta )$为$X$的概率分布律$P(X=x),x=x_1,x_2,...$）,$f$形式已知，但是具体参数$\theta$未知。

    • 现在，我们由已知的样本（在神经网络中，样本 的每一个随机变量就是一个数据，整个数据集组成了我们的样本，这个层级别混乱了），建立统计量$\hat{\theta }(X_1,...,X_n)$。对于样本观察值$(x_1,x_2,...,x_n)$,若将 $\hat{\theta }(x_1,...,x_n)$作为$\theta$的估计值，则$\hat{\theta }(X_1,...,X_n)$为参数$\theta$的估计量。（在神经网络算法中，这个估计量就是我们最后确定的预测模型）

    • 注意：$f(x;\theta )$ 这里用的是分号，含义和“逗号”不一样，他表示的是一个“似然函数”，它实际是自变量为$\theta$的函数,所以一般也写做$L(\theta )$。分号前面是抽样得到的确定值,分号后是变量。

4.1.1.2 极大思然估计

前面我们介绍了参数估计，而极大似然估计就是一种重要的参数估计的方法，这个部分我们将具体介绍极大思然估计的方法。

• 极大思然估计的思想：

  我们现在知道，参数估计解决的问题是：已知模型，利用已知样本，估计参数。而极大思然法是如何利用已知样本信息的呢？下面我们会具体展开，首先我们看一下其核心理念的直观理解：

  对于具体的一次抽样，得到了这个样本的一组观察值(观察值的个数越多越好)，一次抽样中，这些事件(指的是每个随机变量的观察值发生的次数的组合)同时发生了，那么，这些事件同时发生的概率$P(X_1=x_1,...,X_n=x_n)$应该很大。所以，我们有理由这么推断：${\theta }_1,{\theta }_2,..,{\theta }_n$的应该取的值，应该是使得$P(X_1=x_1,...,X_n=x_n)$最大的${\theta }_1,{\theta }_2,..,{\theta }_n$，这个过程，就是极大似然估计做的事情。
  接下来，我们从定义出发，一步步推导其表达式：

• 似然函数：设$X$为分布为$f(x;{\theta }_1,{\theta }_2..,{\theta }_k)$，其中${\theta }_1,{\theta }_2..,{\theta }_k$是未知参数，$（X_1,...,X_n）$是来自总体$X$的$简单随机样本$。则：
  $$L({\theta }_1,{\theta }_2..,{\theta }_k)=\prod _{i=1}^{n}f(x_i;{\theta }_1,{\theta }_2..,{\theta }_k)$$
  称为${\theta }_1,{\theta }_2..,{\theta }_k$的似然函数。等式右边原本是联合分布，在简单随机抽样中，有一个重要性质：独立同分布。因此，其联合分布等于边缘分布的乘积，所以，我们直接将各个$x_i$参数的边缘分布相乘即得到联合分布

• 最大似然估计量：就如我们前面介绍的极大似然估计的思想，我们希望得到使得$P(X_1=x_1,...,X_n=x_n)$最大的${\theta }_1,{\theta }_2,..,{\theta }_n$。由这个想法，我们得到了最大似然估计量的表达式：
  $$L({\hat{\theta }}_1,{\hat{\theta }}_2..,{\hat{\theta }}_k)=\underset{{\theta }_1,...,{\theta }_k}{\max }L({\theta }_1,{\theta }_2..,{\theta }_k)=\underset{{\theta }_1,...,{\theta }_k}{\max }\prod _{i=1}^{n}f(x_i;{\theta }_1,{\theta }_2..,{\theta }_k)$$

• 求解方法——对数最大似然：最大似然估计就是我们的最终目标，现在我们剩下的问题是，如何求解，可以看到，最大似然估计的最令人头疼的问题就是$\prod$符号，于是有了对数似然的概念，我们知道 $\ln x$是 $x$的单调上升函数，所以我们对最大似然估计量取对数，其最大值对应的每一个${\theta }_i$的值是一样的，于是，对数似然的概念产生了：
  $$\ln L({\theta }_1,{\theta }_2..,{\theta }_k)=\sum _{i=1}^n\ln f(x_i;{\theta }_1,{\theta }_2..,{\theta }_k)$$
  我们可以求解对数似然方程组，通过这种方式，来得到似然函数的最大值：
  $$\frac{\partial \ln L({\theta }_1,...,{\theta }_k)}{\partial {\theta }_i}=0$$
  注意：这不是神经网络算法所使用的主要方法,因为这方程组的求解对于深层神经网络而言也极其复杂，神经网络的主要求解方式是基于梯度下降的，下面我们具体会说

4.1.2 交叉熵（cross-entropy error）代价函数：

前面说了，实际上，神经网络算法并不是使用传统的求解对数似然方程的方法来求得对数最大似然估计值的，而是使用梯度下降法得到这个估计值。前面已经介绍了梯度下降法，我们简单回顾一下：
梯度下降法是对模型的参数进行估计的方法，使用梯度的反方向作为惩罚值进行逐步迭代，每次迭代都会使得模型越来越接近目标函数的优化目标。
现在，我们回到正题，我们现在要做的是选择代价函数和优化目标，对于代价函数的选择，平均绝对误差(MAE)或者平均平方误差(MSE)是两个比较常用的方案，他通过衡量每个预测值和真实值的差距的累加，来作为目标函数，这是可行的，但是，他存在一定缺陷，也就是容易达到饱和，接下来我们会具体解释。
本章节将从熵的定义出发，结合极大似然法，一步步推导出交叉熵代价函数。 并解释使用交叉熵代价函数的好处。

4.1.2.1 交叉熵，相对熵，KL散度的概念

• 熵：熵是信息论的概念。首先，我们需要明确的是，信息量的定义：信息多少的量度。一般使用$\log n$表示，其中n是某个状态出现次数的度量。
  而熵的本质是香农信息量的期望。按照真实分布p来衡量识别一个样本的所需要的编码长度的期望(即平均编码长度)为：$H(p)={\sum }_i^{}p(i)\times log\frac{1}{p(i)}$ 。这就是熵的公式

• 交叉熵：如果你学过协方差的话，你了解协方差与方差的关系，可以用它来类比交叉熵和熵的关系。现有关于样本集的两个概率分布p和q，我们可以把他直接对应到神经网络的两个分布：p为经验分布，q模型估计分布。如果使用模型估计分布q，来表示来自经验分布p的平均编码长度，则应该是：$H(p,q)=\sum_{i}^{} p(i)\times log\frac{1}{q(i)} $，这就是交叉熵的定义式。我们可以从公式中看到交叉熵的特性：与熵的值比较，可以用来度量两个分布的区别情况，取极端情况来解释。只有在p和q相同时，$H(p,q)=H§$。事实上，根据Gibb{s}^{\prime }inequality可知，$H(p,q)\geq H§$恒成立。

• 相对熵：相对熵定义在交叉熵的基础之上，将交叉熵减去经验分布的熵，即可得到相对熵：
  $$D(p||q)=H(p,q)-H(p)=\sum _{i}p(i)\times log\frac{p(i)}{q(i)}$$

  • 相对熵又称KL散度，这两个是同一个概念(Kullback–Leibler divergence，KLD)

  • 它表示2个函数或概率分布的差异性：差异越大则相对熵越大，差异越小则相对熵越小，特别地，若2者相同则熵为0。

  • 是只有$p(x)=q(x)$时，其值为0。若 $p(x)$和$p(x)$略有差异，其值就会大于0。其证明利用了负对数函数$-\ln x$是严格凸函数（strictly convex function）的性质。具体可以参考PRML 1.6.1 Relative entropy and mutual information.

4.1.2.2 交叉熵代价函数

由相对熵的定义，我们可以将求解极大似然估计量的问题转化成求相对熵最小值的问题，因为他们本质都是衡量相似的指标。下面我们要完成由相对熵的概念到机器学习中的代价函数的最后几个映射。

• 首先，几个前提：

  • 就像前面说的，我们可以把q和p直接对应到神经网络的两个分布：p为经验分布，q模型估计分布。

  • 这里的模型估计分布，指的是我们通过似然函数求得的当前情况下的模型，我们现在要做的就是优化这个模型的参数。经验分布指的是通过输入数据集得到的分布函数

  • 我们使用了$\ln$来代替了信息论经常使用的${\log }_2$

  • 我们调整一下相对熵的表达形式，可以得到：
    $$D(p||q)=\sum _{i}p(i)\times \ln p(i)-p(i)\times \ln q(i)$$

• 接着，由于$p(i)$表示的是经验分布数据，他由输入的数据集决定，不随着梯度下降而改变，所以，在神经网络算法中，考虑将其作为优化目标，则我们可以将上述式子进行再次化简，得到：
  $$D(p||q)=-\sum _{i}p(i)\times \ln q(i)$$
  这个函数形式实际上和交叉熵是一样的**，这就是为什么大家有说用交叉熵做代价函数的，也有说用相对熵做代价函数的。实际上，这两者是同一回事**。

• 如果直接使用上面的式子去预估，我们是无法推导出大家所经常看到的$C=-\frac{1}{n}{\sum }_x[y\ln a+(1-y)\ln (1-a)]$代价函数的，问题在哪呢?

  实际上，我们在这之后做了进一步的近似，即将每一个经验分布的概率$p(i)$近似于$ \frac{1}{n}$，可以得到这个式子：
  $$D(p||q)=-\sum _{i}p(i)\times \ln q(i)\approx -\sum _i\frac{1}{n}\times \ln q(i)$$

• 接着就是最后一步，求出传说中交叉熵代价函数，若我们使用sigmoid函数作为输出单元，则我们可以把$P(x;\theta )=e^{y\ln a+(1-y)\ln 1-a}$得到下面的结果，具体如何得到，请看下章广义线性模型：
  $$D(p||q)=-\frac{1}{n}\sum _x[y\ln a+(1-y)\ln (1-a)]$$

• 到这里我们可以庆祝一下了，因为，我们的得到的基于相对熵的代价函数了！这里补充说明一下，在倒数第二步（也就是还没带入具体模型的时候），我们看到，得到的公式和负数对数极大似然估计的表达式是一样的，唯一的区别就是$\frac{1}{n}$和符号，所以说，如果我们说通过求对数极大似然的最大值来作为优化目标，从结果上也是正确的。但他们的本质来源不太一样。可以说，这是同一个公式的两种解释。

4.1.2.3 交叉熵代价函数的好处

• 已知的最小值为零，容易编程实现：不管是直接求最大的似然函数还是求最小化的KL散度，其本质都是一样的，但是求最小化的KL散度，有一个好处：就如前面所说的，相对熵代价函数是一个最小值为0的函数，这对于软件实现而言，是非常方便的。

• 学习效率提高:通过反向传播算法求偏导之后不会保留一阶偏导项，这是我们使用均方误差(MSE)和平均绝对误差(MAE)所做不到的。我们看sigmoid函数：
  
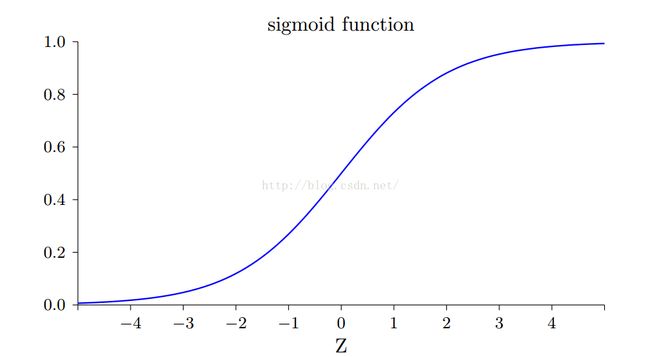
  其只有在y取值为0.5附近时，其偏导项才会比较大，而在0附近或者1附近时，其偏导项很小，这导致我们在计算惩罚项的时候，所能得到的惩罚值很小，导致了学习效率降低。而如果使用相对熵代价函数，则可以消除偏导项，使得惩罚值不会变小。这个的证明我会在下一章介绍广义线性模型之后向大家展示

4.1.3 本节其他参考资料

• 关于熵，交叉熵，相对熵：
  https://www.zhihu.com/question/41252833
  https://www.zhihu.com/question/41252833/answer/141598211
  http://blog.csdn.net/lanchunhui/article/details/50970625
• Cross Entropy 维基百科
  https://en.wikipedia.org/wiki/Cross_entropy
• 相对熵近似的推导：
  http://freemind.pluskid.org/notes/ml/mle/
• 《随机数学基础》 曹振华 编，第七章，参数估计
• 《Deep Learning 》by lan Goodfellow in “5.5 Maximum Likelihood Estimation”

4.2 选择概率分布模型和对应的输出单元

这章我们介绍概率分布模型和对应的输出单元的选择问题，在极大似然估计中，我们还有最后一环没有解决，就是“确定模型，估计参数”中的“模型”是什么？这个概率分布模型确定之后，与之对应的输出单元的激活函数是什么？
在本章节中，我们会介绍广义线性模型，以此为基础来推导常用的输出单元，sigmoid和softmax的函数的来源；并以此为基础，来推导出我们上一章为解决的代价函数最终表达式。
之后，我们会对对比使用MAE和交叉熵作为代价函数两种方式求得误差项的区别，我们会证明，使用交叉熵时，sigmoid和softmax为什么能够避免函数饱和（saturation），也就是误差项太小的问题。

4.2.1 广义线性模型（generalized linear model, GLM）

4.2.1.1 指数族(Exponential family or Exponential class)

• 指数族的作用

  • 首先要明确，指数族和指数分布不一样，指数族是一个满足某一个特定形式的概率分布函数的集合。他有未知的参数，当这些参数确定后，就变成特定的分布了。

  • 他的重要作用是提供了一个分布的模型框架，并且我们可以通过选择特定的**自由参数(natural parameter)来得到特定的分布；通过使用充分统计量(natural sufficient statistics)**来定义这个分布中有用的样本统计量

  • 指数族所能表现的分布集合非常广泛，很多自然界常见的分布都能用指数族表示，包括：正态分布，泊松分布，伯努利分布，伽马分布等等

• 指数族的定义
  $$f_X(X|\mathbf{\theta })=h(X)\exp (\sum _{i=1}^s{\eta }_i(\mathbf{\theta })T_i(X)-A(\mathbf{\theta }))$$
  进一步，我们可以用向量化的表示：
  $$f_X(X|\mathbf{\theta })=h(X)\exp ({\mathbf{\eta }(\mathbf{\theta })}^T\mathbf{T}(X)-A(\mathbf{\theta }))$$
  其中：

  • $X$是随机变量(random variable):
    $$X=(x_1,x_2,...,x_k)$$
    每一个$x_i$是随机变量的观测值

  • $\mathbf{\theta }$模型参数:
    这是一个向量，是用于确定模型最终的分布形式的未知参数,比如泊松分布的参数就是$\lambda$
    $$\mathbf{\theta }=({\theta }_1,{\theta }_2,...,{\theta }_s{)}^T$$
    还有一点很重要：$\theta$的取值必须不会对$X$的取值造成任何限制，这是用来判断一个族是不是指数族的依据。举个例子：对于分布Pareto distribution，有以下限制$x\ge x_m$，$x_m$是一个参数，则$f(x)$依赖于$x_m$这个未知参数，他就不是一个指数分布族。

  • $\mathbf{T}(X)$充分统计量：
    简单理解就是对于任何的随机变量x和y，都可以得到T(x)=T(y)。因为本文不会用到这个参数，一笔带过

  • $\mathbf{\eta }(\mathbf{\theta })$自然参数：
    $\mathbf{\eta }(\mathbf{\theta })=\mathbf{\theta }$是自然参数的标准形式，标准形式不是唯一的，$\mathbf{\eta }(\mathbf{\theta })$可以被乘以任意的非零常量，$T(x)$乘以对应常量的倒数。
    有时候，我们会无视$\mathbf{\theta }$，直接写成$\mathbf{\eta }$。因为$\mathbf{\theta }$不会对分布模型造成本质的改变，这也是$\mathbf{\eta }$被称作自然参数的原因

4.2.2 广义线性模型

4.2.2.1 广义线性模型的直观解释——从线性模型讲起

广义线性模型有两个特征：一个是是传统的线性模型的拓展；一个是利用了指数族分布。维基百科中使用了海滩的例子，个人觉得比较直观，这里也引用海滩的例子进行广义线性模型的直接解释。

• 传统线性模型：首先，传统的线性模型，预测值（又称响应变量，response variable），根据随机变量的观察值的线性组合（又称预测器predictors）而得到。这就意味着，对于预测器常量数量的改变，响应变量也有相对应常量的改变。她要求响应变量服从正态分布(normal distribution)。
  这样的模型具有比较大的局限性，当我们的响应变量并不直接等于预测器的线性组合时，这个模型就不适用了。
  我们以海滩为例：我们希望预测10°C 的温度变化会带来海滩的人数的变化，假设我们的训练的结果是下降1000人，实际上，这个数据和海滩的规模有关系。对于规模小的海滩，实际上会下降10个人；对于规模大的海滩，可能下降10000人。最后的综合结果是1000人。
  如果我们使用线性模型，那些小规模的海滩，比如在高温度时期望来50人的海滩，就会被预测为：温度下降后，会来-950人，这是不合理的。

• 广义线性模型
  实际上，更合理的模型应该是温度可能会对人员的到达率造成影响。可能是温度下降10°C，来的人会减少一半。所以对于原本有50人的期望的海滩，应该来25人；10000人的海滩来5000人。响应变量和预测器程指数关系。
  如果我们希望响应变量的分布不是正态分布。并且使用任意函数(后面会提到，是连接函数(link-function)）来使得响应变量和预测变量成线性变化（而不是需要假设响应变量和预测变量本身是线性关系的）。这就是广义线性模型做的事情。

• 广义线性模型在机器学习中如何使用：

  • 作为优化目标的似然函数：首先我们需要确定一个概率模型，也就是极大似然法中我们所“已知”的模型，具体表现形式为概率分布似然函数$P(X;\theta )$。我们通过广义线性模型可以得到某种分布的概率分布函数，代入代价函数进行优化。
  • 作为生成对应分布的激活函数：通过广义线性模型我们求解给定模型的连接函数，这个连接函数就可以作为激活函数，把预测变量(也就是我们机器学习中的数据集)作为输出层的激活函数的输入，经过链接函数，便能够得到在该模型分布下的输出。
  • 补充说明[个人观点]：那么我们是否一定要用链接函数作为输出层的激活函数呢？我认为是不必要的，如果有其他激活函数的计算性能更好，并且函数形状与标准的链接函数差不多，以损失一定精度为代价，来提高性能，也是可行的。

4.2.2.2 数学定义：

1. 首先，响应变量$Y$必须是指数族分布中的一种。
2. 响应变量$Y$的数学期望$\mu$取决于独立随机变量$X$,$X$便是我们输入的训练数据。满足以下关系：
   $$E(Y)=\mu =g^{-1}(X\beta )$$

• $E(Y)$是$Y$的分布的数学期望，当$Y$的分布已知后，这个量的表达式应该已知。
• $X\beta$是线性预测器，他是$X$和$\beta$的线性组合；$\beta$就是我们使用极大似然法时（或者其他参数估计方法）需要估计的模型未知变量
• $g$是链接函数：用来完成响应变量分布的期望和线性预测器的链接

3. 线性预测器，满足关系：$\eta =X\beta$

• 他通过链接函数和响应变量的期望关联起来，所以称为预测器
• 因为他是由未知参数$\beta$和一直的独立随机变量$X$的线性组合组成。所以叫线性预测器

4.2.3 伯努利分布(Bernoulli Distributions)和Sigmoid 函数单元

4.2.3.1 伯努利分布和广义线性模型

• 伯努利分布的使用场景：伯努利分布又叫做0-1分布，他描述的是这样一种分布，进行一次随机实验，成功的概率为$p$,如果成功的变量取值为1，失败概率为$1-p$，其变量取值为0。对应的概率密度函数为：
  $$P(y|p)=p^y(1-p{)}^{1-y}$$
  回到神经网络中，我们之前说了，在极大思然估计时，我们需要确定一个概率分布模型，所以，当我们面对的输出是一个二分类问题的时候，我们的模型选用的就是伯努利分布模型，而未知的参数为$\beta$。

• 伯努利分布和广义线性模型：接下来，我们将伯努利分布写成指数分布族的形式：

  \begin{align*}
  P(y|p)&=p ^y (1-p)^{1-y}\
  &=\exp(\ln {(p ^y (1-p)^{1-y})})\
  &=\exp(y\ln p + (1-y)\ln (1-p))\
  &=\exp(y\ln \frac{p}{1-p} + \ln (1-p))
  \end{align*}
  对比指数分布族的模型的定义，我们可以得到
  $$\eta =\ln \frac{p}{1-p}$$
  我们接下来求链接函数$g$，首先我们知道伯努利分布的期望$E(Y)=\mu =p$，根据广义线性模型的第二点要求，可得：
  $$g(\mu )=X\beta$$
  根据线性预测器的定义，可知：
  $$X\beta =\eta =\ln \frac{p}{1-p}$$
  由$\mu =p$，我们可得：
  $$g(\mu )=\ln \frac{\mu }{1-\mu }$$
  转化为关于$X\beta$的函数，可得
  $$f(X\beta )=g^{-1}(X\beta )=\frac{1}{1+e^{-X\beta }}$$
  其中$\beta$在我们常见表达式中是权重$W$，我们把他改写一下，就是我们常见的sigmoid了：
  $$h(z)=h(W^{T}X)=g^{-1}(W^{T}X)=\frac{1}{1+e^{-W^{T}X}}$$
  可能你会问，偏置单元呢？实际上，偏置单元已经隐含在其中了，我们把W增加一列代表b，并且与之对应多一行X的值恒为1,就可以转为这个表达形式了
  小结：大家看到了，这就是sigmoid函数的由来了，总结一下：在神经网络中，如果我们的输出单元处理的是一个二分类问题，对应的就是伯努利分布就是我们所需要分布函数模型。
  之后，我们通过广义线性模型得到了sigmoid函数。以sigmoid函数作为输出单元的激活函数，得到的结果的概率分布就是伯努利分布，便可以使用对应的代价函数作为优化目标。

4.2.3.2 sigmoid为激活函数的交叉熵代价函数的推导后续

接着，我们回头看一下我们之前推导sigmoid交叉熵代价函数的时候跳过的一个步骤，在4.1.2.2 最后，我们得到了我们的优化目标是这个：
$$\underset{\theta }{\min }J(\theta )=\underset{\theta }{\min }-\frac{1}{n}\sum _x\ln P(x;\theta )$$
而我们前面所说，使用sigmoid函数的概率分布是伯努利分布，也就是前面我们推导出来的：
$$P(y;\theta )=\exp (y\ln p+(1-y)\ln (1-p))$$
而连接函数的表达式如下：
$$h(z)=h(W^{T}X)=g^{-1}(W^{T}X)=\frac{1}{1+e^{-W^{T}X}}$$
为了方便理解，我们将其转化成神经元激活函数的表达形式$z={\theta }^{T}x+b$，得到：
$$\begin{gathered} h(z)=\frac{1}{1+e^{-z}} \\ 其中，z={\theta }^{T}x+b \end{gathered}$$
接着，我们将$P(y;\theta )$带入$J(\theta )$之后，得到：
$$J(\theta )=-\frac{1}{n}\sum _x(y\ln h(z)+(1-y)\ln (1-h(z)))$$
这就是sigmoid神经元的神经网络代价函数。

4.2.3.3 梯度下降法的进一步推导：交叉熵解决函数饱和(saturates)问题

• sigmoid+MSE得到的梯度项：
  使用MSE代价函数：
  $$J(y;\theta )=\sum _x(y-h(z){)}^2$$
  我们对任意一个梯度项${\theta }_i$求导：
  $$\frac{\partial J}{\partial {\theta }_i}=\sum _{x}2(y-h(z))h^{{}^{\prime }}(z)x_i$$
  问题就在$h^{{}^{\prime }}(z)$，我们看一下sigmoid函数，我们一起回忆一下sigmoid函数：

你会发现，他的一阶导数项只有在$y=0.5$附近才比较大，其余地方会比较小，导数项的值较小，将导致我们的惩罚值较小，降低学习效率，也也就是饱和问题。

• 使用交叉熵代价函数如何解决：
  我们来看sigmoid的交叉熵代价函数：
  $$J(\theta )=-\frac{1}{n}\sum _x(y\ln h(z)+(1-y)\ln (1-h(z)))$$
  同样，我们对任意一个梯度项${\theta }_i$求导，这里需要用到sigmoid导数的一个性质：
  $$h^{{}^{\prime }}(z)=h(z)(1-h(z))$$
  所以，我们得到：
  KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ \frac{\partial…
  带入梯度下降法的公式，得到梯度更新的最终公式：
  $${\theta }_i^{{}^{\prime }}={\theta }_i-ϵ\frac{1}{n}\sum _x{x}_i(h(z)-y)$$
  可以看到，当y=1时，只有z是非常大的正数，才能接近饱和；当y=0时，只有z是非常小的负数，才接近饱和。

4.2.4 其他输出层的激活函数单元

4.2.4.1 多项分布和广义线性模型

• 多项分布的使用场景：当我们希望我们的模型的输出是一系列，比如有$n$个的离散量，每个离散量有自己的出现的概率，这样的场景，对应的就是多项分布，其对应的激活函数就是softmax函数，其表达式如下：
  $$softmax(z{)}_i=\frac{\exp (z_i)}{{\sum }_{j}exp(z_j)}$$
  其中，各个离散量的概率和为1：
  $$\sum _{i}softmax(z{)}_i=1$$
• 多项分布和广义线性模型：
  多项式分布也可以用同样的方法的到softmax分布，并且，在交叉熵代价函数解决过饱和问题，原理类似，就不多做推导

4.2.4.2 其他分布和对应单元

除了提到的这两种常用分布外，其他的分布大家可以参考维基百科下面的例子：
https://en.wikipedia.org/wiki/Exponential_family

4.2.5 本节其他参考资料

• 《Deep Learning 》by lan Goodfellow in “6.3 Hidden Units”
• Generalized linear model 维基百科：
  https://en.wikipedia.org/wiki/Generalized_linear_model
• Exponential family 维基百科：
  https://en.wikipedia.org/wiki/Exponential_family
• 《广义线性模型》 橴樰：
  http://www.cnblogs.com/tbcaaa8/p/4507192.html

4.3 多层网络的梯度如何获得

• 我们还有什么为解决？：如果我们的神经网络是直接从输入到输出，中间只有一个激活函数，那么到这里所有过程都已经完成了，将4.2.3.3得到的
  $$\frac{\partial J}{\partial {\theta }_i}=\frac{1}{n}\sum _x{x}_i(h(z)-y)$$
  带入梯度下降的更新公式：
  $$x_i^{{}^{\prime }}=x_i-ϵ\frac{\partial f(x)}{\partial x_i}$$
  就能得到参数的更新的最终表达式，实际上，这便是Logistic Regression的表达式：
  $${\theta }_i^{{}^{\prime }}={\theta }_i-ϵ\frac{1}{n}\sum _x{x}_i(h(z)-y)$$
  但是，在神经网络中，$f(x)$到$x$不是直接得到的，实际上是经过了很多层的包裹（大家可以回忆一下第二章介绍通用逼近定理时，我们所举的例子），那么怎么办呢？我们当然可以写出每一个的导数的表达式进行梯度更新，但是这样的办法效率很低，有没有更简单的办法呢？这就是梯度下降法所做的事情。

• 本章具体讲神经网络算法，行文结构如下：

1. 首先，介绍反向传播算法大家所理解的常见误区；

2. 为正式介绍反向传播算法做知识储备的铺垫，主要包括：计算图；张量；微积分中的链式法则和其在高维度的推广等几个方面

3. 接着，我们会借助多层感知机来介绍一次反向传播算法中的核心思想：递归使用链式法则

4. 之后，我们会正式介绍反向传播算法（这过程也会介绍前向传播）的实现，我们将以伪代码为主体进行讲解。同时，我们将这个过程分成两个部分：

   • 简单的伪代码实现
   • 更具备通用性的伪代码实现

4.3.1 BP算法的定义理解误区

1. 首先需要明确的是，反向传播算法是用来求解梯度（gradient）的一种方法。比起直接计算梯度的表达式，他所需要消耗的计算资源比较少,速度较快。

2. 反向传播算法是用来计算梯度的，其计算得到的梯度可是被其他算法来使用，比如随机梯度下降法（stochastic gradient descent）。如果你不使用BP算法，你也可以通过直接计算数学表达式来计算梯度，但是这样效率并不高；同样的，你可以可以使用BP算法，但是不使用随机梯度下降法来进行优化，如果你有其他优化方法的话。总之，这是解决问题的两个层面的算法，不能混为一谈

3. 反向传播算法不是专门用于神经网络算法的梯度计算方法，他可以用于任何函数的导数计算。

4.3.2 预备知识

4.3.2.1 张量(tensor)：

前言：张量的更主要用武之地实际上在物理学上，据我理解，神经网络中使用的张量更多的是借其“形”罢了，而实际上，机器学习中所述的张量和物理学中的张量用途有比较大的差别。——这个论断只是我个人的理解，不保证正确。对于物理学的张量我的认知十分有限，所以也不对物理学中的张量做过多的阐述，仅引用看到的一些文字

• 物理学中的张量
  下面摘录两个关于张量的说明：

  • “张量所描述的物理量是不随观察者或者说参考系而变化的，当参考系变化时（其实就是基向量变化），其分量也会相应变化，最后结果就是基向量与分量的组合（也就是张量）保持不变。”
  • “张量有如此强大的表示能力，又不随观察者不同而变化，能够有效的表示宇宙间的万物”
  • “一个量, 在不同的参考系下按照某种特定的法则进行变换, 就是张量”

  所以说，张量更侧重于在高维度中，用不同的参考系可以表示同一个物理量。想更深入了解张量的定义和用途的，可以参考下面两篇知乎问答：

https://www.zhihu.com/question/23720923/answer/32739132
https://www.zhihu.com/question/20695804

• 机器学习的张量
  • 先摆出一个比较直观的例子：
    RGBA图，在数字图像处理中，我们描绘一张图片不是简单的通过行和列来完成的，行列的每一个元素有RGBA四个值。这便是机器学习，数据挖掘领域的一个四维张量的例子。
  • 我们可以把张量理解成一个"多维矩阵"。这是我们用来描绘复杂数据的一种方式。标量是1维张量，向量是二维张量。维度可以理解成坐标系的维度。

4.3.2.2 微积分中的链式法则和其在高维度的推广

• 首先，我们假设$x$是一个标量，$f$和$g$是进行标量到标量的映射的函数，假设$y=g(x),z=f(g(x))=f(y)$，那么，链式法则可以表示为：
  $$\frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}$$

• 进一步推演，我们把形式从标量推演到向量，$x\in R^m$,$y\in R^n$,$z\in R$,也就是说，$g$完成从$R^m$空间到$R^n$子空间的映射。同理，$f$能够完成从$R^n$到$R$的映射，我们将函数转化成简单的标量的形式进行理解：
  $$\begin{gathered} z=f(y_1,y_2,...,y_n) \\ {y}_i=g(x_1,x_2,...,x_m) \end{gathered}$$
  可以看到，我们要求的关于$x_i$的偏导数，$z$的任意一个输入变量$y_j$都是与之相关联的。我们知道，多元微分的复合函数求导法则如下：
  
  所以我们需要对其直接相关的所有输入变量$y_j$求偏导，再乘以其复合的子函数关于$x_i$的偏导，最后将结果累加，便可以得到如下表达式：
  $$\frac{\partial z}{\partial x_i}=\sum _j\frac{\partial z}{\partial y_j}\frac{\partial y_j}{\partial x_i}$$
  进一步抽象，将其转化成向量的表达形式：
  KaTeX parse error: Got function '\bf' with no arguments as subscript at position 18: …igtriangledown _̲\bf{x} z=(\frac…
  其中，$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$是$y$对$x$求一阶偏导数，以一定方式排列成的矩阵，也就是雅可比矩阵（Jacobian Matrix），这是一个nm的矩阵，具体展开，形式如下：
  KaTeX parse error: No such environment: align* at position 55: …}=\left[ \begin{̲a̲l̲i̲g̲n̲*̲}̲ &\frac{\partia…
  而KaTeX parse error: Got function '\bf' with no arguments as subscript at position 18: …igtriangledown _̲\bf{y} z表示的是向量微分形式，这是一个n1的向量：
  KaTeX parse error: Got function '\bf' with no arguments as subscript at position 19: …igtriangledown _̲\bf{x} z=\left[…
  根据公式相乘，就可以得到KaTeX parse error: Got function '\bf' with no arguments as subscript at position 18: …igtriangledown _̲\bf{x} z,这是一个$m\times 1$的向量。

• 我们再进一步，我们知道在机器学习中，我们的算法更多的是基于张量的，而张量就像我们前面所描述的，可以理解成一个多维的矩阵，要明确，这个过程的原理没有什么变化，我们所做的只是一点数据的组织，让他像网格组织起来。我们具体来看：假设$X$是一个$m\times n\times p$的三维张量， KaTeX parse error: Got function '\bf' with no arguments as subscript at position 18: …igtriangledown _̲\bf{X} z用来表示$z$对于$X$求偏导，它的结果仍然是$m\times n\times p$，我们可以理解成我们对该张量的每一个元素进行求导，最后按照张量这个多维矩阵的组织方式，把每一个求得的导数一一填入矩阵的对应位置。
  同样，我们假设$Y$是一个$r\times s\times t$的三维张量，并且，有下面的关系
  $$z=f(Y)=f((Y_1^1{)}_1,(Y_1^2{)}_1,...,(Y_r^s{)}_t)$$
  $$(Y_i^j{)}_k=g(X)=f((X_1^1{)}_1,(X_1^2{)}_1,...,(X_m^n{)}_p)$$，
  与上面的二元符合函数求导一样，我们要做的，就是对每一个函数链求导，相加.以求$\frac{\partial z}{\partial (X_i^j{)}_k}$为例：
  $$\frac{\partial z}{\partial (X_i^j{)}_k}=\sum _a\sum _b\sum _c\frac{\partial z}{\partial (Y_a^b{)}_c}\frac{\partial (Y_a^b{)}_c}{\partial (X_i^j{)}_k}$$
  如果我们使用KaTeX parse error: Got function '\bf' with no arguments as subscript at position 18: …igtriangledown _̲\bf{X} z 表示对整个张量的偏导，便可以化成下面形式
  KaTeX parse error: Got function '\bf' with no arguments as subscript at position 18: …igtriangledown _̲\bf{X} z=\sum_a…
  我们最后，在对$Y$,进行向量化的表达：
  KaTeX parse error: Got function '\bf' with no arguments as subscript at position 18: …igtriangledown _̲\bf{X} z=\sum_j…

4.3.3 深度神经网络中递归使用链式法则

本节借用周志华老师在《机器学习》一书中的一张关于多层感知机的图来讲解一下链式法则是如何在深度神经网络中被应用的。注意，原图是用来讲解浅层神经网络的，我只是利用这个比较简单的例子，来向大家介绍深度神经网络中如何进行递归进行隐藏单元的信息传递的

因为原图没有使用张量化的表达形式，我们的讲解也从最基础的标量形式开始。最后我们做一个从标量到向量，从单层到多层网络的表达形式重述。

• 符号声明：

  • $x$：输入的原始数据，也就是该层网络的输出
  • $v$：输入层到隐藏层的权重
  • $\alpha$：输入层的加权输出：$x$经过线性变换$Vx$得到，也是下一个层次的输入。
  • $b$：我们得到上一层的输出之后，经过激活函数$f(a)$,就能得到$b$，这就是本层的输出；
  • $w$：隐藏层的输出到输出层的输入的权重
  • $\beta $：我们得到隐藏层的输出之后，经过线性变换$Wb$，得到下一层(输出层)的输入，也就是本层的加权输出
  • $y$：输出，我们得到输出层的输入之后，经过输出单元的激活函数$f(\beta )$，便可以得到最后的预测值
  • $f$：激活函数表达式
  • $J$:我们用来优化的代价函数

• 过程梳理：
  大家仔细阅读我的符号声明，可以发现，整个神经网络的操作，分为以下几个步骤重复的出现：i层的输出->经过线性变换后->i+1层的输入(或我把他叫做i层的加权输出，后文也都会这么表述)->经过激活函数->i+1层的输出->经过线性变换… …

• 我们的目标：
  链式法则能让我们比较轻松的得到梯度，但是我们需要拿到哪些梯度呢？我们首先要明确我们的目标：到目前为止，我们能够得到梯度下降的表达式，用于更新模型中的参数，但是不容易直接得到，见前面我们还有什么没解决？，反向传播算法通过链式法则，可以避免直接求偏导数的表达式，具体而言，我们可以通过链式法则求出每个神经元的$\frac{\partial J}{\delta w}$和$\frac{\partial J}{\partial b}$，$b$表达的是偏置单元，这在我们给出的图中没有列出来。

• 如何求$\frac{\partial J}{\partial w}$和$\frac{\partial J}{\partial b}$，以求$\frac{\partial J}{\partial w}$为例:

  • 首先，我们以求图中隐藏层的$\frac{\partial J}{\partial w}$为例：首先，我们知道：
    $${\beta }_j=\sum _h{w}_{hj}{b}_h$$
    我们以$\beta$为复合函数的中间层，即$J(w)=J(\beta (w))$，根据链式法则
    $$\frac{\partial J}{\partial w_{hj}}=\frac{\partial J}{\partial {\beta }_j}\frac{\partial {\beta }_j}{\partial w_{hj}}$$
    ，而$\frac{\partial \beta }{\partial w_{hj}}=b_h=f({\alpha }_h)$，$b_h$数据我们在前项传播过程中就已经得到了。所以可以把他当成已知量，到这里，我们的公式变成：
    $$\frac{\partial J}{\partial w_{hj}}=\frac{\partial J}{\partial {\beta }_j}\frac{\partial {\beta }_j}{\partial w_{hj}}=\frac{\partial J}{\partial {\beta }_j}{b}_h$$

  • 那么，接下来，我们剩下要解决的就是$\frac{\partial J}{\partial {\beta }_j}$,也就是说，是关于代价函数对我们所需求层的加权输出求偏导，我们发现
    $$\hat{y}=f(\beta )$$
    以$f$为复合函数的中间层，即$J(\beta )=J(f(\beta ))$，则可以得到：：
    $$\frac{\partial J}{\partial w_{hj}}=\frac{\partial J}{\partial {\beta }_j}\frac{\partial {\beta }_j}{\partial w_{hj}}=\frac{\partial J}{\partial {\hat{y}}_j}\frac{\partial {\hat{y}}_j}{\partial {\beta }_j}{b}_h$$
    激活函数的导数一般是已知的表达式，所以可以得到：
    $$\frac{\delta \hat{y}}{\partial \beta }=f^{{}^{\prime }}(\beta )$$
    而$\beta$数据在我们前向传播的时候就已经得到了，他代表的是当前层的带权输出项，我们也可以当成一个已知量。
    $$\frac{\partial J}{\partial w_{hj}}=\frac{\partial J}{\partial {\beta }_j}\frac{\partial {\beta }_j}{\partial w_{hj}}=\frac{\partial J}{\partial {\hat{y}}_j}\frac{\partial {\hat{y}}_j}{\partial {\beta }_j}{b}_h=\frac{\partial J}{\partial {\hat{y}}_j}{f}^{{}^{\prime }}(\beta )b_h$$

    • 至此，我们剩下的部分是$\frac{\partial J}{\partial \hat{y}}$，这代表的是代价函数和我们所需求层的神经元输出求偏导。 对于输出层而言，这个式子已经有答案了，因为关于代价函数$J$的表达式是给定的，所以我们只要求其偏导的值就行了。最后，我们就能得到这个常见的表达式：
      $$\frac{\partial J}{\partial w}=\frac{\partial J}{\partial \hat{y}}\frac{\partial \hat{y}}{\partial \beta }\frac{\beta }{w}=J^{{}^{\prime }}(\hat{y})f^{{}^{\prime }}(\beta )h(a)$$
    • 最后，如果现在后一层不是输出层，而仍然还是隐藏层，我们则还需要继续推导。我们现在以输入层为例重新推导一遍，现在我们要求$\frac{\partial J}{\partial v}$，重复前面过程，我们得到
      $$\frac{\partial J}{\partial v_{ih}}=\frac{\partial J}{\partial b_h}\frac{\partial b_h}{\partial {\alpha }_h}\frac{\partial \alpha }{\partial v_{ih}}$$
      t同理，这个式子中，除了$\frac{\partial J}{\partial b_h}$，其他我们已经可以求得了，所以我们现在要解决最后一个问题，代价函数和我们所需求层的神经元输出求偏导，在现在这个情况中，并不能直接被求出来，但是我们根据函数复合的原理，可以知道，对于某一个$b_h$,有：
      KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲ J(b_h)=J(\beta…
      根据求导的链式法则，我们可以推出：
      $$\frac{\partial J}{\partial b_h}=\sum _{j=1}^l\frac{\partial J}{\partial {\beta }_j}\frac{\partial {\beta }_j}{\partial b_h}$$
      这里出现了一件非常有趣的事情：前者$ \frac{\partial J}{\partial \beta_j}$是我们在前面计算过程中已经求得的，而后者$\frac{\partial \beta_j}{\partial b_h}=w_{hj}$，直接是一个已知量，直观看起来是什么呢？他等于与该神经元相关的所有下一层的加权输出的偏导乘以他们俩之间的权重，最后求和。
      $$\frac{\partial J}{\partial v_{ih}}=\sum _{j=1}^l\frac{\partial J}{\partial {\beta }_j}{w}_{hj}{f}^{{}^{\prime }}({\alpha }_h)x_i$$

  • 上面这步，就是深度神经网络在隐藏层中递归传递的关键了，我们成功找到了反向传播算法的递归单元，就是：代价函数和我们所需求层的后一层加权输出求偏导$ \frac{\partial J}{\partial \beta}$，剩下的其他我们所需要的数据，都可以通过进行额外的简单计算得到结果。我们将在下面重述一遍这个过程。

• 总结重述：

  • 最后重述中，我们会用矩阵形式的表达，以便衔接之后的算法。我们先做一下符号说明：
    • $J$:代价函数
    • $a^{(l)}$第$l$层神经网络单元加权后的输出，$a^{(l)}=(W^{(l)}{)}^T{h}^{(l-1)}+b^{(l)}$，$l\in \{1,2,...,n\}$
    • $h^{(l)}$:第$l$层神经元输出，$h^{(l)}=f(a^{(l)})$,$l\in \{0,1,...,n\}$,$h$的层数比a,b,k多一层，因为还算上了输入层
    • $f$：激活函数
  • 首先明确：在反向传播算法中，我们需要递归使用的是代价函数关于我们需求层的后一层加权输出的偏导，假设我们现在计算$l$层的数据，我们最终将复用$ \bigtriangledown_{a^{(l+1)}} J$，得到$ \bigtriangledown_{a^{(l)}} J$。我们首先能够得到$\bigtriangledown_{h^{(l)}} J$。如果我们下一层是输出层：
    $${▽}_{h^{(l)}}J={▽}_{\hat{y}}J$$
    如果不是输出层，由已知的表达式关系：
    $$a^{(l+1)}=(W^{(l+1)}{)}^T{h}^{(l)}+b^{(l+1)}$$
    根据链式法则，其乘以$(W^{(l+1)}{)}^T$，也就是连接$l$的输出和$l+1$输入的权重：
    $${▽}_{h^{(l)}}J=(W^{(l+1)}{)}^T{▽}_{a^{(l+1)}}J$$
    注意这里使用了向量化的表述形式：我们把$n\times 1$的列向量$W^{(l+1)}$转置之后，与${▽}_{a^{(l+1)}}J$这个同样是$n\times 1$ 的列向量相乘，就可以得到每个元素相乘，最后求和的效果。
  • 之后，由：
    $$h^{(l)}=f(a^{(l)})$$
    我们乘上$l$层输出关于输入的偏导$f^{{}^{\prime }}(a^{(l)})$,就可以得到代价函数关于我们需求层的加权输出的偏导，
    $${▽}_{a^{(l)}}J=f^{{}^{\prime }}(a^{(l)})\odot {▽}_{h^{(l)}}J$$
    这里，我们也进行了向量化，$\odot$ 是点乘，完成的操作是两个相同尺寸的向量的对应元素相乘。
    到这里，我们已经完成的递归使用的过程。
  • 最后，再根据我们所要计算的$w^{(l)}$和$b^{(l)}$乘上对应的偏导数，由
    $$a^{(l)}=(W^{(l)}{)}^T{h}^{(l-1)}+b^{(l)}$$
    前者为$ h^{(l-1)}$后者为常数1。就可以得到我们所需要的所有偏导项了:
    $${▽}_{w^{(l)}}J=h^{(l)}{▽}_{a^{(l)}}J=h^{(l-1)}{f}^{{}^{\prime }}(a^{(l)})\odot ((W^{(l+1)}{)}^T{▽}_{a^{(l+1)}}J)$$
    $${▽}_{b^{(l)}}J={▽}_{a^{(l)}}J=f^{{}^{\prime }}(a^{(l)})\odot ((W^{(l+1)}{)}^T{▽}_{a^{(l+1)}}J)$$

4.3.4 反向传播算法的伪代码

本节的算法来自《Deep Learning》教材，我们以伪代码为例，进一步分析算法的实现。

4.3.4.1 基于全连接的多层感知机的伪代码

• 前馈传播过程
  

  • 目的：
    • 前馈传播过程我们要达到的目的，首先是计算每一个网络层次的加权输出$a^{(k)}$；
    • 其在激活函数中生成的输出数据$h^k=f(a^{(k)})$以此求得最后的预测值$\hat{y}$。
    • 并且，以此为基础计算代价函数$J$，在代价函数中，我们包含了之前讲到的交叉代价熵代价函数$L(\hat{y},y)$以及用来修正的正则项$\lambda \Omega$。后者主要用来修正优化过程的偏差，在本文中不具体展开。
  • 变量描述在算法过程中，要注意几个变量：
    $x$是原始的输入数据；$h$是每一层神经元的输出数据（还未计算$W$）；在输入层中，他与每一个$x$一一对应；在隐藏层和输出层中，他等于上一层的输出$h^{(k-1)}$经过权重$W$和偏置单元$b$做线性变换，得到该层网络的输入$a$（也就是上一层网络的权输出），带入激活函数$f$之后得到的结果。
  • 在算法执行过程中，我们并不是以每一个单元为单位进行计算的，而是以整个层为单位进行计算的，所以大家看到的$a^k,h^k,\hat{y}$都是向量而不是简单的标量；我们以向量化计算的方式的目的是，他能够在代码实现时减少计算量。
  • 这个过程中，我们需要存储以下几个数据，为反向传播服务：$a$, $J$, $\hat{y}$, $h$.

• 反向传播过程
  

• 目的：

  • 反向传播过程中，我们要做的就是计算每一层对应的参数的梯度项${▽}_{b}L$和${▽}_{W}L$
  • 需要注意的是，这里的算法表达也都是向量化的表达，每个变量代表的都是向量或者是矩阵

• 几个重要的计算过程：

  • 首先$g$是用于暂存得到梯度项的变量。它的的更新的起点是代价函数关于输出的偏导，我们通过求代价函数对$\hat{y}$的偏导数${▽}_{\hat{y}}L(\hat{y},y)$。

  • 这里要注意的一点是，正则项不直接参与反向传播链式法则的计算中，所以大家看到我们一开始求梯度时是基于${▽}_{\hat{y}}L(\hat{y},y)$，而不是$J$。正则项是在链式法则计算完毕后，在求${▽}_{b}L$和${▽}_{W}L$时，才分别加上$\lambda {▽}_{b^{(k)}}\Omega (\theta )$和$\lambda {▽}_{W^{(k)}}\Omega (\theta )$

  • 之后，我们需要利用我们在前馈传播中得到的每一层的输入数据$a$，根据我们前面推到的链式法则，我们可以递归的求解代价函数关于本层的带权输出的偏导值：
    $${▽}_{a^{(l-1)}}J=f^{{}^{\prime }}(a^{(l)})\odot {▽}_{h^{(l)}}J$$

  • 之后，我们根据公式：
    $${▽}_{W^{(l)}}J=h^{(l-1)}{▽}_{a^{(l)}}J$$
    $${▽}_{b^{(l)}}J={▽}_{a^{(l)}}J$$
    计算了${▽}_{w^{(l)}}J$和${▽}_{b^{(l)}}J$，并使用了正则项进行修正。

  • 最后，我们根据我们得到的$\bigtriangledown_{a^{(l)}} J $，求得\ast \ast 代价函数关于本层的输出(不加权)的偏导值\ast \ast$\bigtriangledown_{h^{(l-1)}} J$，赋值给$g$供前一层的网络使用，这个步骤通过以下公式实现：

$${▽}_{h^{(l-1)}}J=(W^{(l)}{)}^T{▽}_{a^{(l)}}J$$

4.3.5 [补充]基于计算图的更通用的反向传播伪代码

对于理解反向传播算法而言，前一节所提到整个思路已经包含了反向传播算法的主要思想，本节是对BP算法重新进行表述，使之更具备通用性：

• 上一个算法是基于全连接的，我们希望我们的算法能够对于每一个节点$z$，能够到达他反向传播所能达到的每一个可达到的路径，并且通过对到达该节点的所有路径的梯度进行加权求和。
• 同时，我们希望我们的算法是基于张量的，不仅仅是标量，向量。

4.3.5.1 上一节的代码的改进空间

对于理解反向传播算法而言，前一节所提到整个思路已经包含了反向传播算法的主要思想，本节是对BP算法重新进行表述，使之更具备通用性：

• 上一个算法是基于全连接的，我们希望我们的算法能够对于每一个节点z，能够到达他反向传播所能达到的每一个可达到的路径，并且通过对到达该节点的所有路径的梯度进行加权求和。
• 同时，我们希望我们的算法是基于张量的，不仅仅是标量，向量。

最后，这个部分我们只表述反向传播过程，不对前馈传播做赘述。

4.3.5.1 计算图(Computational Graphs)

• 定义：
  • 目的：计算图是用来精确的描述反向传播算法的形式化的语言
  • 成分：
    • 节点(node)：图中的每一个节点指向一个变量。
    • 变量(variables)：可以是一个标量、矩阵或者张量或者其他
    • 操作(operation)：操作在计算图中表现形式就是边(edge)，他是一个简单的函数，比如我们前面所说的sigmoid等，他有多个变量作为输入，一个变量作为输出。有以下几点需要注意的：
• 函数比操作更为复杂，他可能包含一个或者多个操作组成；
• 在实际的神经网络实现中，我们的输出不一定是一个变量，可能是多个变量（比如同时输出index和value等），但是为了避免理解混乱，我们将他定义为唯一的变量作为输出。

4.3.5.2 举例说明

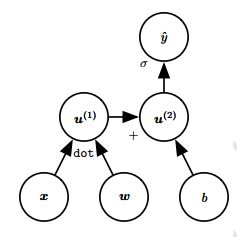
这是一个计算图的例子，我们可以看到，该计算图以$w$、$x$和$b $ 为输入，最后计算的是$ \hat{y} $,其对应的函数表达式是：$\hat{y}=\sigma{(x^Tw+b)}$

4.3.6.1 反向传播过程

我们还是以解释代码为导向，来解释我们的算法。

• 类型说明：

  • 变量(variables):为了保证最大的算法的通用性，我们规定所有的变量都是张量，张量包括了标量、向量和矩阵
  • $\mathcal{G}$：代表计算图，是一个图的数据结构，图中的每一个节点是一个变量(variable)。每一个边是一个操作(operation)
  • 在计算图中，儿子(children)指的是边的箭头指向的节点；反之则为父母(parent)

• 算法的执行框架部分：
  

  • 变量说明
    • T：T是我们需要计算梯度的一组变量的集合，这些变量是图中的一个个节点
    • $z$：这是我们需要计算微分的最根的节点的标量；
    • $\mathcal{G}$是网络架构完整的计算图；
    • ${\mathcal{G}}^{{}^{\prime }}$是那些$z$的子节点，并且属于$T$的节点的，并且是$z$的祖先的图
  • 流程说明：
    • 这个伪代码只是一个BP算法的驱动器，做的事情就是遍历所有的需要求梯度的点，计算他们的梯度，计算结果会被存储在$\mathcal{G}$中。

• build_grad算法的具体实现部分：
  

  • 变量说明
    • V：本轮需要计算梯度的节点
    • $\mathcal{G}$是网络架构完整的计算图。
    • ${\mathcal{G}}^{{}^{\prime }}$是那些$z$的子节点，并且属于$T$的节点的，并且是$z$的祖先的点。用来限制参加梯度计算的节点。
    • grad_table:用来存储每个节点的梯度，他有一个索引项，索引的内容就是节点。
    • **get_consumers($V,{\mathcal{G}}^{{}^{\prime }}$)**用来获取当前节点的儿子节点（也就是全连接层时网络的后一层）
    • get_inputs($C,{\mathcal{G}}^{{}^{\prime }}$)。用来获取当前节点的父亲节点（也就是全连接层时网络的前一层）
    • op$\leftarrow$ get_operation($C$)，用来获取C节点对应的数据结构，他应该是一个指向节点的类的一个实例对象的指针，为了保证我们算法的通用性，我们假设$C$的种类是多种多样的，这就意味着我们生成C的算法不一样，C的偏导数的求法不一样，我们将这些具体实现相关的东西封装在类的内部，当我们使用op.bprop来计算梯度项时，只需要调用封装好的接口即可
    • op.bprop(inputs,$X$,$G$):用来执行反向传播的操作，根据公式：
      KaTeX parse error: Got function '\bf' with no arguments as subscript at position 18: …igtriangledown _̲\bf{X} z=\sum_j…
      这里我们的对应表达是：
      KaTeX parse error: Got function '\bf' with no arguments as subscript at position 18: …igtriangledown _̲\bf{X} z=\sum_j…
      公式解释：
      • inputs应该用于计算当前操作的输出输入变量集合；
      • op.f 是该计算节点的对应操作；
      • $G_i$作为输入，是已经求好的梯度项
      • $X$ 是我们要计算的梯度项的分母
  • 算法流程：
    下面，我们以这个网络计算图，来模拟算法执行过程
    

    • 首先，我们明确，每次执行build_grad操作，获得的是$V$的梯度项，现在我们开始，计算图中$V$的梯度：

    • 正式开始之前，先做预判，如果该梯度已经求过了，就直接返回

    • 接着，我们需要获得当前节点的所有儿子节点$C_1,C_2,C_3$，并且获得所有$C_i$的实例，以方便下一步操作，现在我们先进入$C_1$

    • 我们再次调用build_grad，得到$C_1$对应的梯度项的值，如果此时$C_i$已经计算好了，那么进入前面的预处理步骤就能直接返回，我们可以避免重复计算。而在全连接层网络中，我们规定了网络之间明确的层次关系，每次计算某个层次网络的梯度项时其所依赖的梯度项已经计算完毕，也避免了这个递归调用的而过程。现在我们假设$C_1$的梯度项已经计算完毕

    • 获取$C_i$的所有父亲节点$V,F_1,F_2$，这步骤的目的就是用于求$C_i$节点的函数表达式，以便于之后求导，就像我们之前在全连接网络所求的$f^{{}^{\prime }}(a^{(l)})=f^{{}^{\prime }}(WX+b)$，这里做的，就是拿到$X$的操作。

    • 把$C_i$的父亲节点，当前要求梯度的节点$V$，儿子节点已经求好的梯度$D$带入brop函数，就能得到$C_i$关于$V$的梯度项$G^{(i)}$。最后，我们累加所有的梯度项，就可以得到当前的节点梯度了。在之前的全连接层例子中，还记得吗?我们使用这个公式解决了这个问题：
      $${▽}_{h^{(l)}}J=(W^{(l+1)}{)}^T{▽}_{a^{(l+1)}}J$$

    • 之后，就是做一些数据的赋值和函数返回操作。

4.4 参考资料

• 怎么通俗地理解张量?
  White Pillow的回答
  https://www.zhihu.com/question/23720923/answer/32739132
• 什是事张量？
  andrew shen的回答
  https://www.zhihu.com/question/20695804
• 《机器学习》 周志华 第五章 神经网络
• 《Deep Learning 》by lan Goodfellow in “6.5 Back-Propagation and Other Differentiation Algorithms”

5. 前馈传播过程：隐藏层激活函数

神经网络算法的整体分析已经完成了，本章中，我们将结合前面所述的原理介绍隐藏层的激活函数应该具有怎样的性质，并对常见的激活函数的特点进行简要的分析。
用哪种类型的激活函数作为隐藏层，是还没有定论的事情（但是ReLu通常是一个比较通用的选项）。我们一般通过交叉验证法来检验我们的算法的性能表现。

本章节会介绍以下几个部分的内容：

1. 神经网络的隐藏层激活函数应该具有什么性质
2. 介绍ReLu 单元和maxout单元
3. 比较logistic sigmoid 单元和tanh单元

5.1 激活函数期待具有的性质

明确激活函数的主要作用：增加非线性性，这个是必要的条件，我们甚至用他表达更复杂的特性（比如卷积），目的是使得神经网络能够更好、更快地拟合经验分布函数。从这个角度看，他解决的问题和之后提到的输出层的激活函数本质上略有不同

5.1.1 非线性

这个观点我们在上一章2.1.2 从非线性讲起：为什么使用激活函数中已经具体阐述了，激活函数的存在意义：他希望能够增加模型的非线性性，只有满足了这个条件，神经网络的通用逼近性质才成立，神经网络才有可能拟合一个非线性函数，所以这也是我们选择一个激活函数必须满足的标准之一。

5.1.2 只有有限个离散点不可微(non-differentiability)

在梯度下降法中，我们需要使用激活函数的梯度项来计算每一个单元的惩罚值。
$$x^{{}^{\prime }}=x-ϵ{▽}_{x}f(x)$$
因此，理论上，我们要求激活函数是处处可微的，实际上，一些隐藏层的单元并不是对于所有的输入点都可微的。比如max{0,z}，在z=0的时候不可微。这似乎将导致基于梯度的学习算法不再适用。但在生产实践中，这样的隐藏层单元的表现依然良好，原因如下：

• 神经网络不会真的训练到最小值，只是逐步减少他的值。所以我们不期望得到梯度为0的点，这也是可接受的

• 数学定义左导数右导数都存在且相等为可微。但是计算机不会因为其中一个导数不存在而报错，他通常返回其中一边的导数，所以不用完全意义的可微，也可以使得学习算法得以正常运行

• 计算机，只要可微点有限，离散，我们就可以忽略那些不可微点，选择其为隐藏层单元的激活函数

5.1.3 有限范围

我们希望激活函数的输出是在某一个有限范围内的(比如sigmoid输出是在(0,1))。学习的过程会更加的稳定，激活函数的输出对于权重的影响是有限的；相反的，如果激活函数输出不在一个有限范围内，权重的更新就会变得非常的不稳定，这可能使得学习更加高效，但是我们通常也会使用更小的学习速率或者其他方法来抑制他；

5.1.4 接近恒等函数

接近恒等函数说明他的不是线性函数，但是长得和线性函数差不多，我们可以认为同时具有以下特点的函数是接近恒等函数的：
KaTeX parse error: No such environment: align* at position 7: \begin{̲a̲l̲i̲g̲n̲*̲}̲ f(0)=0,\\ f^{'…

接近恒等函数的好处当它的权重用小的随机值初始化时，神经网络将有效地学习。 当激活函数在原点附近没有这个特征时，在初始化重量时需要考虑特例情况。这个在下面sigmoid函数和tanh函数的比较中具体说明。

5.2 线性整流单元(Rectified Linear Units)和其衍生单元

5.2.1 ReLu

• 形式(图片来自百度百科)：
  
  其表达式为：$$g(z)=\max (0,z)$$
• 特点：
  • 容易优化：他的右边是一个线性函数，当单元被激活（数输入大于零）时，导数一直保持着比较大的数据。并且是一个常数。
  • 死亡(dead)：当输入小于0时，梯度失效。比如当学习率过大时，将可能导致ReLU无法被激活或者在训练过程中死亡。
• 使用技巧：
  可以使其偏置单元$b$被初始化为略大于0的数字，比如0.1。这样，几乎所有的激活函数都会被激活。

5.2.2 ReLU的扩展

• 基于去掉零斜率的拓展：
  这种隐藏单元在$z_i<0$时，使用额外的非零斜率$a_i$来代替原本的0斜率，来避免ReLU容易死亡的特点：
  $$h_i=g(z,\alpha {)}_i=max(0,z_i)+{\alpha }_{i}min(0,z_i)$$
  当$a_i=-1$时，得到
  $$g(z)=|z|$$
  这是Absolute value unit。
  当${\alpha }_i$使用一个比较小的数据，比如0.01，就得到 leaky ReLU
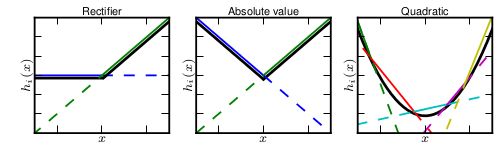
  当把${\alpha }_i$当成一个可以学习的参数时，就得到parametric ReLU
• Maxout:
  • 定义：
    把$z$分成有$k$个值的组，每个组计算自己组的输出$z_j$，取最大的输出，对应表达式：
    $$g(z{)}_i=\underset{j\in G^{(i)}}{\max }{z}_j$$
    $i$代表该神经元是该层网络的第$i$个神经元，其中$G^{(i)}$是我们划分的分组，对于第$i$组，我们把索引项为$\{(i-1)k+1,...,ik\}$的“隐隐层神经元”放进这组，在下图中就是黄色的小神经元，一共有$k$个。
  • 执行过程：
    下面我根据这张图来讲解Maxout的执行过程，图片来自(Maxout Network)
    
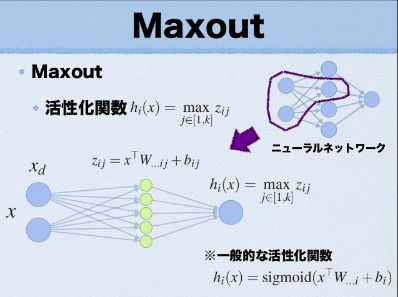
    紫色部分使用的激活函数就是maxout函数，我们可以将这个maxout等价为左下角这个网络，相当于激活函数内部有个隐藏层，这里中间有5个神经元，这说明我们使用的分组$k=5$，接下来，我们需要为每个隐藏的神经元分配一套参数$w_i,b_i$，接下来，计算每个分组的$z$：
    $$z_{ij}=x^T{W}_{ij}+b_{ij}$$
    $i$代表的是当前层（指的是隐藏层）的激活函数的下标；$j$是分组下标，接着，我们可以求得：
    $$g(z{)}_i=\underset{j\in G^{(i)}}{\max }{z}_j=\max (z_{i1},z_{i2},z_{i3},z_{i4},z_{i5})$$
    我们可以看到，他每个小的神经元是一个线性函数，有自己的一套参数。所以他做的是一个k段分段线性函数，这就是他可学习的原因。
  • 特点:

    1. 这是一个可学习的激活函数。根据发明作者证明，只要有1个maxout函数（前提是允许一个maxout函数有无穷小神经元），就可以逼近任意函数

    2. 如果一个maxout有两个以上的分组，就可以产生前面所说的线性整流函数和其衍生出来的几个激活函数的效果，就如下图所述，这个很好理解，因为他实际上就是一个任意多段的分段线性函数：
       

    3. 有k个参数向量而不是1个，所以比起ReLU需要更多的正则化。当然，如果训练集够大，并且分组比较小，不用正则化也是可以的；

5.2.3 ReLU的设计原则

不管使用哪一种ReLU，他的目标和output unit 的目标不太一样。他保证线性，或者说尽量线性。在这个基础上，尽量的提高优化速度，降低优化难度。

5.3 Logistic Sigmoid 和 Hyperbolic Tangent

5.3.1 logistic Sigmoid

• 定义：
  sigmoid这个函数我们之前介绍很多了，其表达式为：
  $$g(z)=\frac{1}{1+e^{-z}}$$
  $$g^{{}^{\prime }}(z)=g(z)(1-g(z))$$
• 特点：

  • 由于他的一阶导数容易饱和的原因（推导见前面证明），一般不建议在隐藏层中作为激活函数。但是在输出层，如果我们调整一下代价函数，比如使用交叉熵代价函数，解决饱和问题，那么，我们可以使用他作为代价函数

  • 在Recurrent network，和其他某些概率模型中。如果我们对激活函数有排除分段线性特征的要求，那么我们仍然会使用sigmoid，尽管他有饱和问题。

5.3.2 双曲切线函数：tanh

• 定义：
  $$g(z)=tanh(z)=\frac{2}{1+e^{-2z}}-1$$
  $$g^{{}^{\prime }}(z)=1-g(z{)}^2$$
  他的函数图如下所示：

  

  • 特点:
    • 他和sigmoid函数有密切的关联
      $$g(z)=2\sigma (2z)-1$$