随机梯度下降，批量梯度下降，牛顿法，拟牛顿法

转载地址：http://blog.csdn.net/lilyth_lilyth/article/details/8973972

转载地址：http://blog.csdn.net/z5718265/article/details/51599175

梯度下降（GD）是最小化风险函数、损失函数的一种常用方法，随机梯度下降和批量梯度下降是两种迭代求解思路，下面从公式和实现的角度对两者进行分析，如有哪个方面写的不对，希望网友纠正。

下面的h(x)是要拟合的函数，J(theta)损失函数，theta是参数，要迭代求解的值，theta求解出来了那最终要拟合的函数h(theta)就出来了。其中m是训练集的记录条数，j是参数的个数。

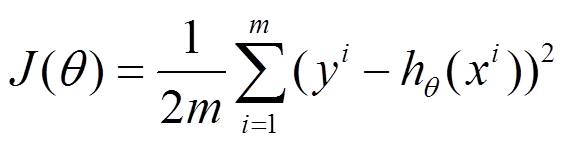
1、批量梯度下降的求解思路如下：

（1）将J(theta)对theta求偏导，得到每个theta对应的的梯度

   

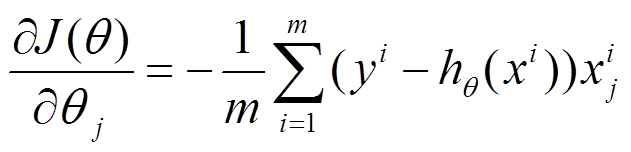
（2）由于是要最小化风险函数，所以按每个参数theta的梯度负方向，来更新每个theta

（3）从上面公式可以注意到，它得到的是一个全局最优解，但是每迭代一步，都要用到训练集所有的数据，如果m很大，那么可想而知这种方法的迭代速度！！所以，这就引入了另外一种方法，随机梯度下降。

2、随机梯度下降的求解思路如下：

（1）上面的风险函数可以写成如下这种形式，损失函数对应的是训练集中每个样本的粒度，而上面批量梯度下降对应的是所有的训练样本：

（2）每个样本的损失函数，对theta求偏导得到对应梯度，来更新theta

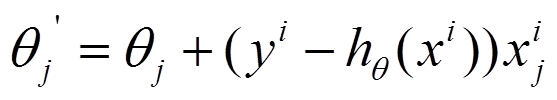
（3）随机梯度下降是通过每个样本来迭代更新一次，如果样本量很大的情况（例如几十万），那么可能只用其中几万条或者几千条的样本，就已经将theta迭代到最优解了，对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。

3、对于上面的linear regression问题，与批量梯度下降对比，随机梯度下降求解的会是最优解吗？

（1）批量梯度下降---最小化所有训练样本的损失函数，使得最终求解的是全局的最优解，即求解的参数是使得风险函数最小。

（2）随机梯度下降---最小化每条样本的损失函数，虽然不是每次迭代得到的损失函数都向着全局最优方向， 但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近。

4、梯度下降用来求最优解，哪些问题可以求得全局最优？哪些问题可能局部最优解？

对于上面的linear regression问题，最优化问题对theta的分布是unimodal，即从图形上面看只有一个peak，所以梯度下降最终求得的是全局最优解。然而对于multimodal的问题，因为存在多个peak值，很有可能梯度下降的最终结果是局部最优。

5、随机梯度和批量梯度的实现差别

以前一篇博文中NMF实现为例，列出两者的实现差别（注：其实对应Python的代码要直观的多，以后要练习多写python！）

 // 随机梯度下降，更新参数
 public void updatePQ_stochastic(double alpha, double beta) {
     for (int i = 0; i < M; i++) {
         ArrayList Ri = this.dataset.getDataAt(i).getAllFeature();
         for (Feature Rij : Ri) {
             // eij=Rij.weight-PQ for updating P and Q
             double PQ = 0;
             for (int k = 0; k < K; k++) {
                 PQ += P[i][k] * Q[k][Rij.dim];
             }
             double eij = Rij.weight - PQ;

             // update Pik and Qkj
             for (int k = 0; k < K; k++) {
                 double oldPik = P[i][k];
                 P[i][k] += alpha
                         * (2 * eij * Q[k][Rij.dim] - beta * P[i][k]);
                 Q[k][Rij.dim] += alpha
                         * (2 * eij * oldPik - beta * Q[k][Rij.dim]);
             }
         }
     }
 }

 // 批量梯度下降，更新参数
 public void updatePQ_batch(double alpha, double beta) {

     for (int i = 0; i < M; i++) {
         ArrayList Ri = this.dataset.getDataAt(i).getAllFeature();

         for (Feature Rij : Ri) {
             // Rij.error=Rij.weight-PQ for updating P and Q
             double PQ = 0;
             for (int k = 0; k < K; k++) {
                 PQ += P[i][k] * Q[k][Rij.dim];
             }
             Rij.error = Rij.weight - PQ;
         }
     }

     for (int i = 0; i < M; i++) {
         ArrayList Ri = this.dataset.getDataAt(i).getAllFeature();
         for (Feature Rij : Ri) {
             for (int k = 0; k < K; k++) {
                 // 对参数更新的累积项
                 double eq_sum = 0;
                 double ep_sum = 0;

                 for (int ki = 0; ki < M; ki++) {// 固定k和j之后,对所有i项加和
                     ArrayList tmp = this.dataset.getDataAt(i).getAllFeature();
                     for (Feature Rj : tmp) {
                         if (Rj.dim == Rij.dim)
                             ep_sum += P[ki][k] * Rj.error;
                     }
                 }
                 for (Feature Rj : Ri) {// 固定k和i之后,对多有j项加和
                     eq_sum += Rj.error * Q[k][Rj.dim];
                 }

                 // 对参数更新
                 P[i][k] += alpha * (2 * eq_sum - beta * P[i][k]);
                 Q[k][Rij.dim] += alpha * (2 * ep_sum - beta * Q[k][Rij.dim]);
             }
         }
     }
 }

1.牛顿法

在上一节中我们发现，如果在移动的步长中考虑了误差函数的二阶导数，误差函数收敛的速度非常快。其实 z′′(x) 已经不能看做步长了，因为梯度下降法中的步长指的是沿着梯度方向走多远的距离，而那个神奇的方法的迭代公式是： 

xk+1=xk−αz′(x)z′′(x)

只不过我们令 α=1 罢了。我们发现自变量的移动方向已经不是梯度方向了，而是一个“修正”的梯度方向——牛顿方向。 
这一公式的严格推导是这样的：若误差函数在 z(x) 二阶导数连续，将 z(x) 在 xk 处作Talor展开： 

z(x)=z(xk)+z′(xk)(x−xk)+z′′(xk)2(x−xk)2+O((x−xk)2)z′(x)≃z′(xk)+z′′(xk)(x−xk)

令 z′(x)=0 ，得到： 

xk+1=xk−z′(xk)z′′(xk)

 
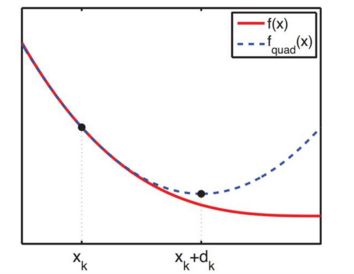牛顿法的实质是在当前位置，使用二次函数来逼近拟合误差函数，认为二次函数的最低点就是误差函数的最低点，在误差函数为严格凹的条件下， z′′(xk)>0 ，保证向误差下降的方向移动，这样反复迭代，就是在逼近真实的最低点。 
上面的公式描述的是一维情况，推广到高维情况公式如下： 

xk+1=xk−H(xk)−1▽z(xk)

即用梯度代替一阶导数，Hessian阵代替二阶导数。

2.牛顿法的问题

一旦出现了Hessian阵的逆，一个随之而来的问题就是当前的Hessian阵是否是可逆的。这是牛顿法一个很大的问题。 
另一个不容易注意到的问题是，Hessian阵是否是一个正定阵，如果Hessian阵是一个负定阵，算法就是在向一个错误的方向收敛。 
第三个问题是求解矩阵的逆是一个 O(n3) 时间复杂度的问题，所以这会成为一个限制求解速度的瓶颈。 
由于这三个问题的存在，牛顿法并不是一个好的优化方法，那么大家自然想到了能不能找到一个严格正定且可逆的阵来近似这个Hessian阵的逆矩阵呢？

3.拟牛顿方法:DFP

我们再来写一次上面Talor展开的高维版本。记误差函数 z(xi) 的梯度为 g(xi) ，海森阵为 H(xi) ，那么在 xi 处的Talor展开如下： 

z(x)=z(xi)+(x−xi)Tg(xi)+12(x−xi)TH(xi)(x−xi)+O((x−xi)2)

等式两边求导得： 

g(x)=g(xi)+H(xi)(x−xi)

令 x=xi−1 ，即上一轮迭代的点，得： 

g(xi−1)=g(xi)+H(xi)(xi−1−xi)g(xi−1)−g(xi)=H(xi)(xi−1−xi)H(xi)−1(gi−gi−1)=xi−xi−1

这里的简写记号 gi 代表 g(xi) 。 
我们把最后一个式子简写为： 

Ci△gi=△xi

我们之前谈过，计算一个矩阵的逆是非常耗费时间的，我们不想去计算 Ci ，而想找到它的一个迭代公式，可以猜想这个公式如下： 

Ci=Ci−1+ai−1vi−1vTi−1+bi−1ui−1uTi−1

其中 Ci−1 是上次迭代使用的 C 矩阵， vi−1和ui−1 是两个列向量， ai−1和bi−1 是两个未知的比例系数。 
结合上一个公式，构造一个方程组： 

{Ci=Ci△gi=△xiCi−1+αi−1vi−1vTi−1+bi−1ui−1uTi−1  (0)

⇒Ci−1△gi+αi−1vi−1vTi−1△gi+bi−1ui−1uTi−1△gi=△xi   (1)

如果说下面两个等式成立： 

{Ci−1△gi=−bi−1ui−1uTi−1△giαi−1vi−1vTi−1△gi=△xi  (2)

等式(1)就肯定成立。 
通过在方程组(2)中比对系数发现，如果令： 

{vi−1=△xiui−1=Ci−1△gi  (3)

系数就必须等于： 

⎧⎩⎨⎪⎪⎪⎪⎪⎪ai=1vTi−1△gibi=−1ui−1△gi  (4)

该等式中可以写成分数形式且可消去的原因是 vTi−1△gi 是一个实数。 
经过这个推导发现，只要按照(3)(4)来设置列向量和系数，方程组(0)就一定成立。有 C 矩阵的迭代公式如下： 

Ci=Ci−1+△xi(△xi)T(△xi)T△gi−(Ci−1△gi)(Ci−1△gi)T△gTiCi−1△gi

有了迭代公式，我们把初始的 C 设置成单位阵 I ，把每次的迭代值作为该点处Hessian矩阵逆矩阵的近似，如此就不需要计算矩阵的逆，所以这就是一个不错的近似方法。

4.拟牛顿方法：BFGS

由DFP的迭代公式： 

{Ci△gi=△xiCi=Ci−1+αi−1vi−1vTi−1+bi−1ui−1uTi−1⇒Ci=Ci−1+△xi△xTi△xTi△gi−(Ci−1△gi)(Ci−1△gi)T△gTiCi−1△gi

互换 g 和 x ，得： 

{△gi=Hi△xiHi=Hi−1+αi−1vi−1vTi−1+bi−1ui−1uTi−1⇒Hi=Hi−1+△xi△xTi△xTi△gi−(Hi−1△gi)(Hi−1△gi)T△gTiHi−1△gi  (5)

接下来如何求海森阵的逆呢？ 
根据 Sherman−Morrison 公式：若 A 是 n 阶可逆矩阵， u 和 v 是 n 维列向量，且 vTA−1u≠−1 ，则： 

(A+uvT)−1=A−1−A−1uvTA−11+vTA−1u

在（5）式中应用两次 Sherman−Morrison 公式，便可以得到 BFGS 方法 C 矩阵的迭代公式 

Ci=(I−△xi△gTi△gTi△xi)Ci−1(I−△gi△xTi△gTi△xi)+△xi△xTi△gTi△xi

下面是DFP方法的Python代码：

# -*- coding: utf-8 -*-
"""
Created on Thu Jul 14 11:59:56 2016

@author: zhangweijian
"""
import numpy as np,math

class Matrix_C(object):

    def __init__(self,a,ERR,ERR_D):
        self.a = a                               #之前一次迭代的自变量
        self.ERR = ERR                           #目标误差函数
        self.ERR_D = ERR_D                       #目标误差函数的导数
        self.n = len(a)                          #自变量的个数
        self.C = np.identity(self.n)             #之前一次迭代的C矩阵，初始值为单位阵
        self.xl = []                  #设定一个记录自变量变化过程的列表

    def next_C(self,x):
        g_d = np.matrix(self.ERR_D(x)-self.ERR_D(self.a))        #本次迭代梯度变化值
        x_d = np.matrix(x - self.a)                         #本次迭代自变量变化值

        denominator = x_d.T*g_d                          #计算两者的点乘，即迭代公式中的分母denominator
        if math.fabs(denominator)<1e-14:             #如果分母denominator过小，则不可作为除数，直接返回单位阵
            return np.identity(self.n)
        A = x_d*x_d.T/denominator                            #迭代公式中第一个添加的矩阵

        denominator_2 = g_d.T*self.C*g_d
        if math.fabs(denominator_2)<1E-14:
            return np.identity(self.n)
        B = (self.C*g_d)*(self.C*g_d).T/denominator_2        #迭代公式中第二个添加的矩阵

        nextC = self.C+A-B                             #本轮计算使用到的C矩阵
        self.C = nextC                                      #更新上一轮迭代的C矩阵,和自变量
        self.a = x
        return nextC

    def start(self):
        self.xl.append(np.matrix(self.a).tolist())
        x = self.a - 0.001*self.C*np.matrix(self.ERR_D(self.a)) #第一次还不能使用next_c函数，从第二次迭代才可以使用
        self.xl.append(x.tolist())
        for i in range(7):
            x = x - self.next_C(x)*np.matrix(self.ERR_D(x))
            print u"第%02d次迭代误差函数的值：%11.8f"%(i+1,self.ERR(x)[0,0]),
            print u'迭代产生的自变量值%+9.8f,%+9.8f'%(x.flatten()[0,0],x.flatten()[0,1])
            self.xl.append(x.tolist())
def Err(x):
    return 3*(x[0]+1)**2+4*(x[1]+2)**2

def Err_D(x):
    t = 6*(x[0]+1),8*(x[1]+2)
    return np.array(t).reshape(-1,1)

DFP = Matrix_C(np.array([40,50]).reshape(-1,1),Err,Err_D)
x = DFP.start()

#接下来进行数据可视化

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d

def err(x,y):
    return 3*(x+1)**2+4*(y+2)**2

x,y = np.mgrid[-60:60:300j,-60:60:300j]
z = err(x,y)
plt.contourf(x,y,z,cmap=plt.cm.gray,levels=[0,20,40,80,120,160,250,330]+range(400,20000,800),alpha=0.6)
h = []
l = []
z = []
for i in DFP.xl:
    h.append(i[0][0])
    l.append(i[1][0])
for x,y in zip(h,l):
    z.append(err(x,y))
plt.scatter(h,l,c='r',s=40)
plt.plot(h,l)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

梯度下降和拟牛顿法是近似计算中非常重要的两种优化方法，在机器学习中有非常广泛的应用，可以在不丧失太多精确性的条件下快速得到最优解。