unity 五种旋转方式localEulerAngles、eulerAngles、rotation、localRotation和Rotate的区别
1.1 transform.localEulerAngles
使用localEulerAngles进行旋转的时候,我们要使用transform.localEulerAngles = new Vector3(x, y,z); 其中,new Vector(x,y,z)为游戏物体最终旋转到的目标角度,x.y,z的值分别都是以0为基准,假设游戏物体的初始角度为(x1,y1,z1),则游戏物体从(x1,y1,z1)旋转到(x,y,z),但是是以父游戏物体的坐标系为参考(自己是顶级游戏物体除外)
举个例子:
假如游戏物体A,B,都没有父游戏物体,B初始旋转角度为(0,0,0),A的初始旋转角度为(0,0,45),编写脚本并把它挂载到B上,脚本编写如下:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class Test2 : MonoBehaviour {
private float agent;
void Start () {
agent = 0f;
}
// Update is called once per frame
void Update () {
agent += Time.deltaTime*50;
transform.localEulerAngles= new Vector3(0f,agent,0f);
}
}
这时,在程序还在跑着的时候,把B拽到A下,作为A的子游戏物体,这时,B的旋转角度为(0f,agent,0f),结果证明也是这样,如下动图:
结论:通过
transform.localEulerAngles= new Vector3(0f,agent,0f);
设置的角度是相对角度(类似于相对路径)
1.2 transform.eulerAngles
transform.eulerAngles= new Vector3(x,y,z)
new Vector(x,y,z)为游戏物体最终旋转到的目标角度,x.y,z的值分别都是以0为基准,假设游戏物体的初始角度为(x1,y1,z1),则游戏物体从(x1,y1,z1)旋转到(x,y,z),,同时也以世界坐标系为参考,而不是以父级游戏物体的坐标系为准。
举个例子:
假如游戏物体A,B,都没有父游戏物体,B初始旋转角度为(0,0,0),A的初始旋转角度为(0,0,45),编写脚本并把它挂载到B上,脚本编写如下:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class Test2 : MonoBehaviour {
private float agent;
void Start () {
agent = 0f;
}
// Update is called once per frame
void Update () {
agent += Time.deltaTime*50;
transform.eulerAngles= new Vector3(0f,agent,0f);
}
}
这时,在程序还在跑着的时候,把B拽到A下,作为A的子游戏物体,这时,你猜,B的旋转角度是如何变化?
如果是以父级游戏物体的坐标系为准为准的话,那么B的旋转角度为(0f,agent,0f)
但是,事实证明,B的旋转角度不仅仅是y轴的值变,连x轴、z轴的值都在变,如下动图:
结论:通过
transform.eulerAngles= new Vector3(x,y,z)
设置的角度是绝对角度(类似于绝对路径)
2.1 transform.rotation
//将欧拉旋转角转换为四元素旋转角
Quaternion rotation= Quaternion.Euler(new Vector3(x, y,z));
Transform.rotation=rotation;
new Vector(x,y,z)为游戏物体最终旋转到的目标角度,x.y,z的值分别都是以0为基准,假设游戏物体的初始角度为(x1,y1,z1),则游戏物体从(x1,y1,z1)旋转到(x,y,z),,同时也以世界坐标系为参考,而不是以父级游戏物体的坐标系为准。
举个例子:
假如游戏物体A,B,都没有父游戏物体,B初始旋转角度为(0,0,45),A的初始旋转角度为(0,0,45),编写脚本并把它挂载到B上,脚本编写如下:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class Test2 : MonoBehaviour {
private float agent;
void Start () {
agent = 0f;
}
// Update is called once per frame
void Update () {
agent += Time.deltaTime*50;
transform.rotation = Quaternion.Euler(new Vector3(0f,agent,45f));
}
}这时,在程序还在跑着的时候,把B拽到A下,作为A的子游戏物体,这时,你猜,B的旋转角度是如何变化?
如果是以父级游戏物体的坐标系为准为准的话,那么B的旋转角度为(0,agent,45f)
但是,事实证明,B的旋转角度不仅仅是y轴的值变,连x轴、z轴的值都在变,如下动图:
结论:通过
Quaternion rotation= Quaternion.Euler(new Vector3(x, y,z));
Transform.rotation=rotation;
设置的角度是绝对角度(类似于绝对路径)
2.2 transform.localRotation
类似于localEulerAngles,不再叙述
3 transform.Rotate(参数)
transform.Rotate(x,y,z):以自身坐标系为参考,而不是世界坐标系,分别以x度y度z度绕X轴、Y轴、Z轴匀速旋转
transform.Rotate(轴,Space.Self):以自身坐标系为参考
Transform.Rotate(轴,Space.World):以世界坐标系为参考
还有其它四种方式就不一一介绍了
3月3日补充:
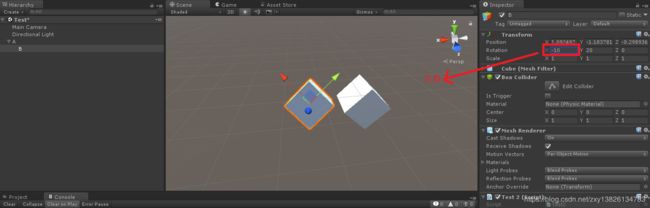
需求:我想拿到下面图中游戏物体B的相对与游戏物体A的三维坐标 (0,20,0)
只需通过 游戏物体B实例对象. transform.localEulerAngles 即可拿到,打印输出如下:
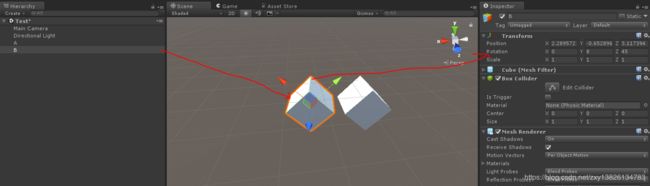
但是当B的坐标出现有负数呢?如下图:
打印输出为:
不知你有没有看出点什么?
是不是有这样的规律:
360+(-10)=350,360+20=380(即为20),360+0=360(即为0)
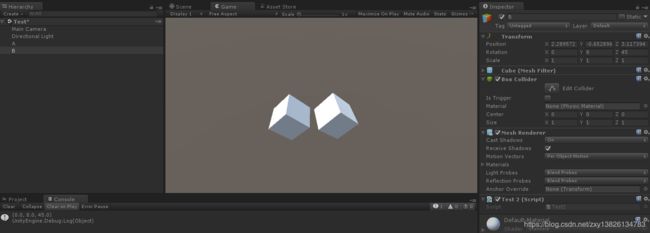
当游戏物体B不再是A的子物体时,如下图:
是否还能通过这种方式获取呢?
答案是肯定的,如下图: