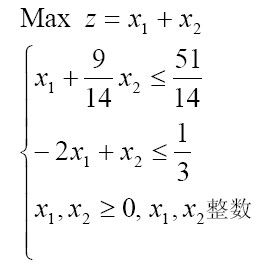LinGo基本用法总结
一、界面及基本用法
所有代码在 Lingo Model - Lingo 1中编写,写完后点击工具条上的红色的靶子运行
线性整数规划
model:
max=x1+x2;
x1+9/14*x2<=51/14;
-2*x1+x2<=1/3;
@gin(x1);@gin(x2);
end
求得x1=3,x2=1,最大值为4.运用matlab求时可以发现有两组解:x1=3,x2=1和x1=2,x2=2。通过验证也可知这两组解均满足。Lingo的一个缺陷是:每次只能输出最优解中的一个(有时不只一个)。那么,怎样求得其他解呢?一个办法是将求得的解作为约束条件,约束x1不等于3,x2不等于1,再求解。如下:
model:
max=x1+x2;
x1+9/14*x2<=51/14;
-2*x1+x2<=1/3;
@gin(x1);@gin(x2);
@abs(x1-3)>0.001;
@abs(x2-1)>0.001;
end
求得x1=2,x2=2.若再次排除这组解,发现Lingo解不出第三组解了,这时我们可以断定:此优化模型有两组解:
x1=3,x2=1和x1=2,x2=2.
求解模型时需注意:Lingo中,默认变量均为非负;输出的解可能是最优解中的一组,要判断、检验是否还有其他解(根据具体问题的解的情况或用排除已知最优解的约束条件法)。
二、常用函数及运算符
1、LINGO具有9种逻辑符号
#not# 否定该操作数的逻辑值,#not#是一个一元运算符
#eq# 若两个运算数相等,则为true;否则为flase
#ne# 若两个运算符不相等,则为true;否则为flase
#gt# 若左边的运算符严格大于右边的运算符,则为true;否则为flase
#ge# 若左边的运算符大于或等于右边的运算符,则为true;否则为flase
#lt# 若左边的运算符严格小于右边的运算符,则为true;否则为flase
#le# 若左边的运算符小于或等于右边的运算符,则为true;否则为flase
#and# 仅当两个参数都为true 时,结果为true;否则为flase
#or# 仅当两个参数都为false 时,结果为false;否则为true
这些运算符的优先级由高到低为:
高 #not#
#eq# #ne# #gt# #ge# #lt# #le#
低 #and# #or#
例:
2 #gt# 3 #and# 4 #gt# 2,其结果为假(0)。
2、Lingo中关系运算符
在LINGO中,关系运算符主要是被用在模型中,来指定一个表达式的左边是否等于、小于等于、或者大于等于右边,形成模型的一个约束条件。关系运算符与逻辑运算符截然不同,前者是模型中该关系运算符所指定关系的为真描述,而后者仅仅判断一个该关系是否被满足:满足为真,不满足为假。
LINGO有三种关系运算符:“=”、“<=”和“>=”。LINGO中还能用“<”表示小于等于关系,“>”表示大于等于关系。LINGO 并不支持严格小于和严格大于关系运算符。
3、数学函数
LINGO提供了大量的标准数学函数
@abs(x) 返回x 的绝对值
@sqrt() 开方
@sin(x) 返回x 的正弦值,x 采用弧度制
@cos(x) 返回x 的余弦值
@tan(x) 返回x 的正切值
@exp(x) 返回常数e 的x 次方
@log(x) 返回x 的自然对数
@lgm(x) 返回x 的gamma 函数的自然对数
@sign(x) 如果x<0 返回-1;否则,返回1
@floor(x) 返回x的整数部分。当x>=0 时,返回不超过x 的最大整数;当x<0
时,返回不低于x 的最大整数。
@smax(x1,x2,…,xn) 返回x1,x2,…,xn 中的最大值
@smin(x1,x2,…,xn) 返回x1,x2,…,xn 中的最小值
变量界定函数
变量界定函数实现对变量取值范围的附加限制,共4种
@bin(x) 限制x 为0 或1 — 用于0-1规划
@bnd(L,x,U) 限制L≤x≤U
@free(x) 取消对变量x 的默认下界为0 的限制,即x 可以取任意实数
@gin(x) 限制x 为整数
在默认情况下,LINGO 规定变量是非负的,也就是说下界为0,上界为+∞。@free 取消
了默认的下界为0的限制,使变量也可以取负值。@bnd用于设定一个变量的上下界,它也可 以取消默认下界为0的约束。
概率函数
1 . @pbn(p,n,x) 二项分布的累积分布函数。当 n 和(或)x 不是整数时,用线性插值法进行计算。
2.@pcx(n,x) 自由度为n的χ2分布的累积分布函数。
3.@peb(a,x) 当到达负荷为 a,服务系统有 x 个服务器且允许无穷排队时的 Erlang 繁忙概率。
4.@pel(a,x) 当到达负荷为 a,服务系统有 x 个服务器且不允许排队时的 Erlang 繁忙概率。
5.@pfd(n,d,x) 自由度为 n 和 d 的 F 分布的累积分布函数。
6.@pfs(a,x,c) 当负荷上限为 a,顾客数为 c,平行服务器数量为 x 时,有限源的 Poisson 服务系统的 等待或返修顾客数的期望值。a 是顾客数乘以平均服务时间,再除以平均返修时间。当 c 和 (或)x 不是整数时,采用线性插值进行计算。
7.@phg(pop,g,n,x) 超几何(Hypergeometric)分布的累积分布函数。pop 表示产品总数,g 是正品数。从 所有产品中任意取出 n(n≤pop)件。pop,g,n 和 x 都可以是非整数,这时采用线性插值 进行计算。
8.@ppl(a,x)Poisson 分布的线性损失函数,即返回 max(0,z-x)的期望值,其中随机变量 z 服从均值 为 a 的 Poisson 分布。
9.@pps(a,x) 均值为 a 的 Poisson 分布的累积分布函数。当 x 不是整数时,采用线性插值进行计算。
10.@psl(x) 单位正态线性损失函数,即返回 max(0,z-x)的期望值,其中随机变量 z 服从标准正态 分布。
11.@psn(x) 标准正态分布的累积分布函数。
12.@ptd(n,x) 自由度为 n 的 t 分布的累积分布函数。
13.@qrand(seed) 产生服从(0,1)区间的拟随机数。@qrand 只允许在模型的数据部分使用,它将用拟随机 数填满集属性。通常,声明一个 m×n 的二维表,m 表示运行实验的次数,n 表示每次实验所 需的随机数的个数。在行内,随机数是独立分布的;在行间,随机数是非常均匀的。这些随 机数是用“分层取样”的方法产生的。
14.@rand(seed) 返回 0 和 1 间的伪随机数,依赖于指定的种子。典型用法是 U(I+1)=@rand(U(I))。注 意如果 seed 不变,那么产生的随机数也不变。
集循环函数
其语法为
@function(setname[(set_index_list)[|conditional_qualifier]]:
expression_list);
@function相对应于下面罗列的四个集循环函数之一;setname是要遍历的集;set_index_list是集索引列表;conditional_qualifier 是用来限制集循环函数的范围,当集循环函数遍历集的每个成员时,LINGO都要对conditional_qualifier 进行评价,若结果为真,则对该成员执行@function操作,否则跳过,继续执行下一次循环。expression_list是被应用到每个集成员的表达式列表,当用的是@for函数时,expression_list 可以包含多个表达式,其间用逗号隔开。这些表达式将被作为约束加到模型中。当使用其余的三个集循环函数时, expression_list 只能有一个表达式。如果省略set_index_list ,那么在expression_list中引用的所有属性的类型都是setname集。
- @for
该函数用来产生对集成员的约束。基于建模语言的标量需要显式输入每个约束。@for函数允许只输入一个约束,然后LINGO 自动产生每个集成员的约束。
!具体用法:
例:
sets:
r/1..8/:d;
c/1..8/:; !就算没有集合属性也要写":";
link(r,c):x,y; !派生集合;
endsets
@for(r(i):@for(c(j):x(i,j)<=y(i,j))); !可用@for(link:x<=y)代替;
@for(r(i)|i#ge#2:d(i)>=3) !":"前说的是对哪个集合进行约束,":"后面说的事具体是什么样的约束;
!"|"表示过滤,即筛选r(i)下标集中i>=2的下标,即/2,3..8/;
plus:lingo注释方法;
!注释内容;
- @sum
该函数返回遍历指定的集成员的一个表达式的和。 - @min和@max
返回指定的集成员的一个表达式的最小值或最大值。
金融函数:
@fpa(I,,n):返回一个现值,其单位时间利率为I,连续支付n个时间段,该支付所对应的现值。
示例程序如下:
贷款金额 50000 元,贷款年利率 5.31%,采取分期付款方式(每
年年末还固定金额,直至还清)。问拟贷款 10 年,每年需偿还多少元?
50000 = x * @fpa(.0531,10)
@fpl(I,n):返回如下情形的净现值,单位时间的利率为I,第n个时间段支付单位费用的现值,可以认为对它求和得到@fpa(I,n)的值。
辅助函数
@if(logical_condition,true_result,false_result)
@if 函数将评价一个逻辑表达式logical_condition,如果为真返回true_ result,
否则返回false_result。
@warn(’text’,logical_condition)
如果逻辑条件logical_condition为真,则产生一个内容为’text’的信息框。
@text(’…/data.txt’)=xx; 将xx的值输入到相应路径下的文件中
参考:
https://wenku.baidu.com/view/9da2f6bff8c75fbfc67db215.html
https://blog.csdn.net/coco_happy1314/article/details/82078742
https://blog.csdn.net/lancecrazy/article/details/78306154
https://blog.csdn.net/gnoixl/article/details/81145892
https://blog.csdn.net/qq_26591517/article/details/50674581
https://blog.csdn.net/lancecrazy/article/details/78306154
https://blog.csdn.net/qq_41196612/article/details/88789605