【keras】利用LSTM进行单变量时间序列预测和多变量时间序列预测

        对于较为简单的时间序列预测问题，可以使用Exponential Smoothing和ARIMA等传统模型非常方便地求解。然而，对于复杂的时间序列预测问题，LSTM不失为一种很好的选择。因此，本文旨在探讨如何利用LSTM神经网络求解时间序列预测问题。首先，需要明白时间序列预测问题是如何转换为传统的监督学习问题的，即时间窗方法。有关时间序列预测问题转换为监督学习的过程请移步：Time Series Forecasting as Supervised Learning。

1.分析时间序列的特点        

        时间序列预测关键：确定已有的时间序列的变化模式，并假定这种模式会延续到未来。下面首先介绍一下时间序列的一般特点，具体请移步：时间序列分析和预测

（1）平稳序列（stationary series）
       基本上不存在趋势的序列，序列中的各观察值基本上在某个固定的水平上波动，在不同时间段波动程度不同，但不存在某种规律，随机波动。

（2）非平稳序列（non-stationary series）
       包含趋势、季节性或周期性的序列，只含有其中一种成分，也可能是几种成分的组合。可分为：有趋势序列、有趋势和季节性序列、几种成分混合而成的复合型序列。

       趋势（trend）：时间序列在长时期内呈现出来的某种持续上升或持续下降的变动，也称长期趋势。时间序列中的趋势可以是线性和非线性。

       季节性（seasonality）：季节变动（seasonal fluctuation）,是时间序列在一年内重复出现的周期波动。销售旺季，销售淡季，旅游旺季、旅游淡季，因季节不同而发生变化。季节，不仅指一年中的四季，其实是指任何一种周期性的变化。含有季节成分的序列可能含有趋势，也可能不含有趋势。

        周期性（cyclicity）：循环波动，是时间序列中呈现出来的围绕长期趋势的一种波浪形或振荡式波动。

        除此之外，还有偶然性因素对时间序列产生影响，致使时间序列呈现出某种随机波动。时间序列除去趋势、周期性和季节性后的偶然性波动，称为随机性（random），也称不规则波动（irregular variations）。

2.单变量时间序列预测

        有关航班乘客流量预测问题的具体细节，请移步：用 LSTM 做时间序列预测的一个小例子

问题：航班乘客预测 
数据：1949 到 1960 一共 12 年，每年 12 个月的数据，一共 144 个数据，单位是 1000 
下载地址 
目标：预测国际航班未来 1 个月的乘客数

'''
Created on 2019年2月16日
    时间序列预测问题可以通过滑动窗口法转换为监督学习问题
@author: Administrator
'''

import numpy
import matplotlib.pyplot as plt
from pandas import read_csv
import math
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
from keras.utils.vis_utils import plot_model

# 创建数据集
def create_dataset(dataset, look_back=1):
    dataX, dataY = [], []
    for i in range(len(dataset)-look_back-1):
        a = dataset[i:(i+look_back), 0]
        dataX.append(a)
        dataY.append(dataset[i + look_back, 0])
    return numpy.array(dataX), numpy.array(dataY)

if __name__ == '__main__':
    # 加载数据
    dataframe = read_csv('international-airline-passengers.csv', usecols=[1], engine='python', skipfooter=3)
    dataset = dataframe.values
    # 将整型变为float
    dataset = dataset.astype('float32')     
    
    # 数据处理，归一化至0~1之间
    scaler = MinMaxScaler(feature_range=(0, 1))
    dataset = scaler.fit_transform(dataset)
    
    # 划分训练集和测试集
    train_size = int(len(dataset) * 0.67)
    test_size = len(dataset) - train_size
    train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
    
    # 创建测试集和训练集
    look_back = 1
    trainX, trainY = create_dataset(train, look_back)           #单步预测
    testX, testY = create_dataset(test, look_back)
    
    # 调整输入数据的格式
    trainX = numpy.reshape(trainX, (trainX.shape[0], look_back, trainX.shape[1]))       #（样本个数，1，输入的维度）
    testX = numpy.reshape(testX, (testX.shape[0], look_back, testX.shape[1]))
    
    # 创建LSTM神经网络模型
    model = Sequential()
    model.add(LSTM(120, input_shape=(trainX.shape[1], trainX.shape[2])))            #输入维度为1，时间窗的长度为1，隐含层神经元节点个数为120
    model.add(Dense(1))
    model.compile(loss='mean_squared_error', optimizer='adam')
    model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=2)
    
    # 绘制网络结构
    plot_model(model, to_file='E:/model.png', show_shapes=True);
    
    # 预测
    trainPredict = model.predict(trainX)
    testPredict = model.predict(testX)
    
    # 反归一化
    trainPredict = scaler.inverse_transform(trainPredict)
    trainY = scaler.inverse_transform([trainY])
    testPredict = scaler.inverse_transform(testPredict)
    testY = scaler.inverse_transform([testY])
    
    # 计算得分
    trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
    print('Train Score: %.2f RMSE' % (trainScore))
    testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
    print('Test Score: %.2f RMSE' % (testScore))
    
    # 绘图
    trainPredictPlot = numpy.empty_like(dataset)
    trainPredictPlot[:, :] = numpy.nan
    trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict
    testPredictPlot = numpy.empty_like(dataset)
    testPredictPlot[:, :] = numpy.nan
    testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict
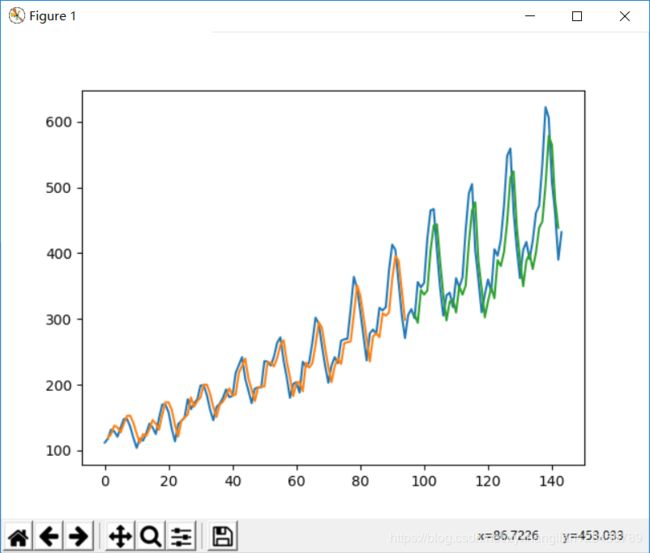
    plt.plot(scaler.inverse_transform(dataset))
    plt.plot(trainPredictPlot)
    plt.plot(testPredictPlot)
    plt.show();

        实验结果：

Using TensorFlow backend.
Epoch 100/100
 - 0s - loss: 0.0022
Train Score: 22.79 RMSE
Test Score: 50.42 RMSE

       注意，在进行数据处理时，将输入trainX改造为LSTM的输入格式，即[samples,timesteps,features]。

3.多变量时间序列预测

        有时，为了充分利用已有的信息，需要利用除了预测变量之外的其他若干个变量同时进行预测，即所谓的多变量时间序列预测。与单变量时间序列预测不同之处在于数据处理。

        例如，对于下述数据集：北京的美国大使馆在2010年至2014年共5年间每小时采集的天气及空气污染指数，其中包括日期、PM2.5浓度、露点、温度、风向、风速、累积小时雪量和累积小时雨量。

        在单变量时间序列预测中，数据通常被处理为下述格式：

   pollution(t-1)  pollution(t)
1   0.129779   0.148893
2   0.148893   0.159960
3   0.159960   0.182093
4   0.182093   0.138833
5   0.138833   0.109658

        然而，在多变量时间序列预测时，数据通常被处理为下述格式： 

   pollution(t-1)  dew(t-1)  temp(t-1)  press(t-1)  wnd_dir(t-1)  wnd_spd(t-1)  \
1   0.129779   0.352941   0.245902   0.527273   0.666667   0.002290
2   0.148893   0.367647   0.245902   0.527273   0.666667   0.003811
3   0.159960   0.426471   0.229508   0.545454   0.666667   0.005332
4   0.182093   0.485294   0.229508   0.563637   0.666667   0.008391
5   0.138833   0.485294   0.229508   0.563637   0.666667   0.009912

   snow(t-1)  rain(t-1)   pollution(t)
1   0.000000        0.0  0.148893
2   0.000000        0.0  0.159960
3   0.000000        0.0  0.182093
4   0.037037        0.0  0.138833
5   0.074074        0.0  0.109658

        多变量时间序列预测的具体实例请移步：基于Keras的LSTM多变量时间序列预测