多项式回归:向线性模型添加非线性
作者:chen_h
微信号 & QQ:862251340
微信公众号:coderpai
介绍
在这篇文章中,我们将学习如何解决线性模型的关键问题,即线性假设。我们将看一下线性回归,这是一种基础统计学习技术,了解模型引擎下发生的事情,然后更多的了解模型的一些弱点。然后,我们将引入多项式回归的思想作为线性模型关键弱点的解决方案,即本文中提出的一种线性回归。
让我们回顾一下线性回归
线性回归是一种机器学习技术,它允许我们将一个或者多个解释变量与自变量或者响应变量进行关联。在线性回归中,我们希望预测实际的数值。
与所有机器学习模型一样,我们试图近似 f(x) ,或者准确描述我们的独立变量和因变量之间关系的函数。指标与交易之间因果关系的建立是所有基于机器学习的交易模型共同的关键特征。在参数模型中,我们通过对函数结构 f(x) 做出一些假设来节省一些时间。在线性回归中,我们假设 f(x) 是线性的。
你可以从代数中回想一下,一条线的方程是 y = mx+b,其中 y 是我的响应,m 是斜率或者是微积分中的导数,b 是我的截距或者是当 x 等于零时 y 的值。
简单线性回归方程如下:
y = B 0 + B i x i + E i y = B_{0} + B_{i}x_{i} + E_{i} y=B0+Bixi+Ei
这里直线的系数只是采用不同的形式,我嗯添加一个误差项 E i E_{i} Ei 。误差项解释了我们无法建模的噪音或者随机性。
虽然现在很多的程序包帮助我抽象掉了大量的计算使得我们的生活变得更容易,但是当我们构建基于机器学习的线性回归模型时,会发生很多事情。我们的目标是近似我们的系数, B 0 B_{0} B0 是我们的截距, B 1 B_{1} B1 是我们的斜率。
一旦我们得到了系数的值,我们就可以将它们插入到我们的线性方程中,这样我们就可以预测给定 X 值的响应值。但是我们如何找到这些系数呢?
我们的斜率等式如下:
B 1 = ∑ i = 1 N ( y i − Y ) ( x i − X ) ∑ i = 1 N ( x i − X ) 2 B_{1} = \frac{\sum_{i=1}^{N}(y_{i} - Y)(x_{i} - X)}{\sum_{i=1}^{N}(x_{i} - X)^{2}} B1=∑i=1N(xi−X)2∑i=1N(yi−Y)(xi−X)
其中 Y 是 y 的平均值,X 是 x 的平均值。
截距 B 0 B_{0} B0 的等式如下:
B 0 = Y − B 1 X B_{0} = Y-B_{1}X B0=Y−B1X
其中 Y 是 y 的平均值, B 1 B_{1} B1 是我们预测的斜率,而 X 是我们解释变量 x 的平均值。
这些计算在 R 和 Python 中使用库和包时,这些计算都是为我们完成的。像往常一样,我们在开发模型时遇到的一个关键问题是我们的测试结果是否与整个样本的结果一致。换句话说,这个样本能代替整个样本的分布,还是只是我们观察到的纯粹的随机。这是我们的统计假设验证技巧的用武之地。简单线性回归的检验统计量如下:
t = B 1 − 0 S E ( B 1 ) t = \frac{B_{1} - 0}{SE(B_{1})} t=SE(B1)B1−0
回归假设我们的 x 和 y 变量之间存在某种关系。因此,我们的假设检验或我们的 H 0 H_{0} H0 的零假设是 B 1 = 0 B_{1} = 0 B1=0 ,我们的替代假设或者 HA 是 H 1 ≠ 0 H_{1} \neq 0 H1̸=0 。本质上,零表示我们的斜率为 0,或者我们的变量之间没有关系。
为了测试这一点,我们计算了 B 1 B_{1} B1 与 0 的偏差。在上面的等式中, B 1 B_{1} B1 是我们预测的斜率,SE( B 1 B_{1} B1 ) 是我们斜率的标准误差。标准误差是衡量斜率偏差的一种方法。
B 1 B_{1} B1 标准误差的等式如下:
S E ( B 1 ) = σ 2 ∑ i = 1 N ( x i − X ) 2 SE(B_{1}) = \frac{\sigma^{2}}{\sum_{i=1}^{N}(x_{i} - X)^{2}} SE(B1)=∑i=1N(xi−X)2σ2
其中, σ 2 = V a r ( E ) \sigma ^{2} = Var(E) σ2=Var(E) 或者是我们的误差项的方差。我们使用我们的数据通过下面的等式计算我们的 RSE 或者残差平方和来估计这个变量:
σ 2 = R S E = R S S ( n − 2 ) \sigma^{2} = RSE = \sqrt \frac{RSS}{(n-2)} σ2=RSE=(n−2)RSS
其中,n 是观测数量,RSS 是我们的剩余平方和。我们的 RSS 可以通过以下等式找到:
R S S = ∑ i = 1 N ( Y i − y i ) 2 RSS = \sum_{i=1}^{N}(Y_{i} - y_{i})^{2} RSS=∑i=1N(Yi−yi)2
其中 Y i Y_{i} Yi 是响应的实际值, y i y_{i} yi 是我们对第 i 次数据的预测值。
我们在简单线性回归的检验统计量对应于高斯分布。因此,一旦我们计算了 t-stat,并指定了显著性水平,我们就可以用来拒绝零假设。请注意,我没有说我会拒绝或接受 null,这是因为未能拒绝 null 并不一定意味着我们接受 null。我们只是无法在某个显著性水平或者某个置信区间内拒绝它。
然后我们得到我们的 p 值。我们的 p 值告诉我们,假设零假设为真,我们有多大可能观察到我们的检验统计值大于或者等于我们观察到的值。换句话说,我们的 p 值告诉我们,假设我们观察到的 t 统计量,我们的零假设的概率是正确的。它也是最低显著性水平,我们可以拒绝零假设 H 0 H_{0} H0 。
在某些情况下,我们不会有单个预测变量,都是有多个变量。这些解释变量可以是定量,变量,也可能是两者的混合。多元线性回归的等式如下:
y = B 0 + B 1 x 1 + B 2 x 2 + … … . . . + B n x n y=B_{0} + B_{1}x_{1} + B_{2}x_{2} + ……... + B_{n}x_{n} y=B0+B1x1+B2x2+……...+Bnxn
多元线性回归的上述方程类似于我们的初始简单线性回归方程,不同之处在于我们现在每个 x 项都有一个斜率 B 1 B_{1} B1 变量。这只是表达了特定 x 和我们的响应 y 之间的关系。
我们的检验统计量和分布也从 t 统计量和高斯分布变成了 f 统计量和 f 分布。
让我们建立一个模型
现在我们已经回顾了线性胡桂,我们可以构建一个模型来进行预测。我们将使用 PNB 数据,我们的目标是预测下一个收盘价。
接下来我们导入一些需要的库:
#data analysis and manipulation
import numpy as np
import pandas as pd
#data collection
import pandas_datareader as pdr
#data visualization
import matplotlib.pyplot as plt
import seaborn as sns
之后我们导入我们的数据:
#setting our testing period
start='2016-01-01'
end='2018-01-01'
pnb=pdr.get_data_yahoo('PNB.NS',start, end)
让我们看看我们的数据长什么样?
pnb.head()
| High | Low | Open | Close | Volume | Adj Close | |
|---|---|---|---|---|---|---|
| Date | ||||||
| 2016-01-01 | 117.900002 | 115.500000 | 116.000000 | 117.599998 | 4070369 | 117.599998 |
| 2016-01-04 | 117.000000 | 112.500000 | 117.000000 | 112.800003 | 6341172 | 112.800003 |
| 2016-01-05 | 113.349998 | 110.199997 | 113.000000 | 110.599998 | 7271156 | 110.599998 |
| 2016-01-06 | 111.800003 | 109.300003 | 110.949997 | 109.599998 | 5910731 | 109.599998 |
| 2016-01-07 | 108.449997 | 104.500000 | 108.099998 | 105.050003 | 7497260 | 105.050003 |
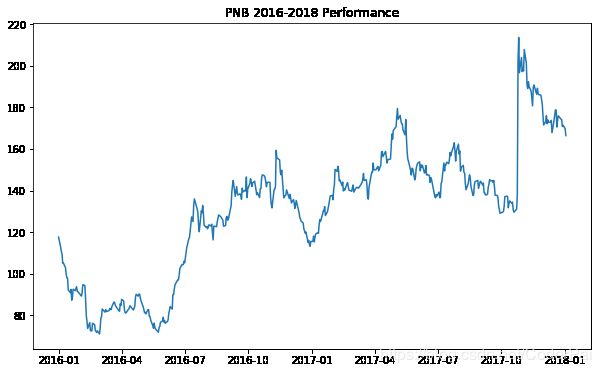
让我们看看 PNB 在我们的样本期间如何表现。
plt.figure(figsize=(10,6))
plt.plot(pnb['Close'])
plt.title('PNB 2016-2018 Performance')
plt.show()
我们现在可以创建解释变量,用于预测 PNB 的收盘价。我们将使用定量和定性变量的混合。
让我们将预测变量添加到数据框中。但首先,我们将复制原始数据帧。如果我们将来需要返回并重新初始化我们的数据,这是一个很好的做法。
#making a copy of our data frame
PNB=pnb.copy()
#creating our predictor variables
#Lag 1 Predictor
PNB['Lag 1']=PNB['Close'].shift(1)
#Lag 2 Predictor
PNB['Lag 2']=PNB['Close'].shift(2)
#Higher High Predictor
PNB['Higher High']=np.where(PNB['High'] > PNB['High'].shift(1),1,-1)
#Lower Low Predictor
PNB['Lower Low']=np.where(PNB['Low'] < PNB['Low'].shift(1),1,-1)
现在让我回顾一下我们的 PNB 数据帧。
PNB.head()
| High | Low | Open | Close | Volume | Adj Close | Lag 1 | Lag 2 | Higher High | Lower Low | |
|---|---|---|---|---|---|---|---|---|---|---|
| Date | ||||||||||
| 2016-01-01 | 117.900002 | 115.500000 | 116.000000 | 117.599998 | 4070369 | 117.599998 | NaN | NaN | -1 | -1 |
| 2016-01-04 | 117.000000 | 112.500000 | 117.000000 | 112.800003 | 6341172 | 112.800003 | 117.599998 | NaN | -1 | 1 |
| 2016-01-05 | 113.349998 | 110.199997 | 113.000000 | 110.599998 | 7271156 | 110.599998 | 112.800003 | 117.599998 | -1 | 1 |
| 2016-01-06 | 111.800003 | 109.300003 | 110.949997 | 109.599998 | 5910731 | 109.599998 | 110.599998 | 112.800003 | -1 | 1 |
| 2016-01-07 | 108.449997 | 104.500000 | 108.099998 | 105.050003 | 7497260 | 105.050003 | 109.599998 | 110.599998 | -1 | 1 |
现在让我们从 scikit-learn 导入我们的线性回归模型。
from sklearn.linear_model import LinearRegression
现在我们有了模型,让我们从 sklearn 导入我们的 train_test_split 对象。
from sklearn.model_selection import train_test_split
现在我们已经准备好为我们的数据创建训练和测试集。但首先,让我们初始化我们的 X 和 y 变量。记住 X 表示我们的预测变量,y 表示我们的响应或者我们实际想要预测的内容。
#creating our predictor variables
X=PNB.drop(['Open','High','Low','Close','Volume','Adj Close'],axis=1)
#initializing our response variable
y=PNB['Close']
现在我们将准备将我们的数据分成训练集合测试集。
X_train, X_test, y_train, y_test= train_test_split(X,y,test_size=.20, random_state=101)
我们现在有我们的训练集和测试集。注意,使用上面的 random_state ,这样当你重新创建此模型时,你将获得与此处相同的输出。
我们现在准备适合我们的模型并作出预测。我们将首先初始化我们的模型。
lm=LinearRegression()
现在我们可以将训练街传递给我们的模型。我们必须先在 X_train 集中填充 NaN 值。
#fitting our model to our training data
lm.fit(X_train.fillna(0),y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
现在我们已经将模型与我们的数据相匹配,让我们使用它来进行预测。我们将 X_test 数据集传递给 predict 方法。X_test 是我们的模型没有看到的数据。
#making predictions
predictions=lm.predict(X_test.fillna(0))
现在我们已经有了预测,我们可以检查一下我们的模型表现如何。我们希望通过各种不同的方式来评估模型的性能。我们的模型的 R2,R-Squared 告诉我们,我们的响应中的百分比方差,可以用我们的预测器来解释。我们还想看看我们模型的错误。我们的错误告诉我们模型偏离实际响应值的程度。我们的目标是创建一个是吸纳最低误差的模型。
我们还可以检查模型的系数。这些是 xi 值每个特征的斜率。
#checking our model's coefficients
lm.coef_
array([ 0.93884112, 0.01779704, 0.32920755, -1.89167465])
让我们得到我们模型的 R2 值。我们将从 sklearn 导入指标。
from sklearn import metrics
#getting our R-Squared value
print('R-Squared:',metrics.explained_variance_score(y_test,predictions))
R-Squared: 0.987638195799
现在让我们检查一下我们的错误。我们将查看我们的MSE,或者均方误差,MAE 或平均绝对误差,RMSE 或者均方根误差。
#printing our errors
print('MSE:',metrics.mean_squared_error(y_test,predictions))
print('MAE:',metrics.mean_absolute_error(y_test,predictions))
print('RMSE:',np.sqrt(metrics.mean_squared_error(y_test,predictions)))
MSE: 11.09225302230123
MAE: 2.485737884039122
RMSE: 3.3305034187493683
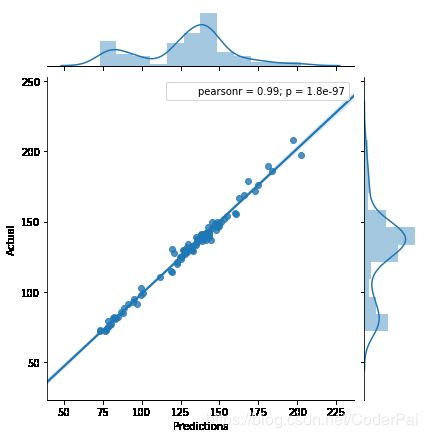
现在让我们绘制我们的实际响应和预测的响应。我们还可以计算残差或者误差。
sns.jointplot(predictions,y_test,kind='regplot')
plt.xlabel('Predictions')
plt.ylabel('Actual')
plt.show()
上图显示我们的预测和实际反应高度相关。它也显示了非常小的 p 值。我们现在绘制我们的残差。
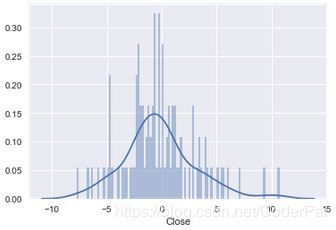
residuals=y_test-predictions
#plotting residuals
sns.distplot(residuals,bins=100)
plt.show()
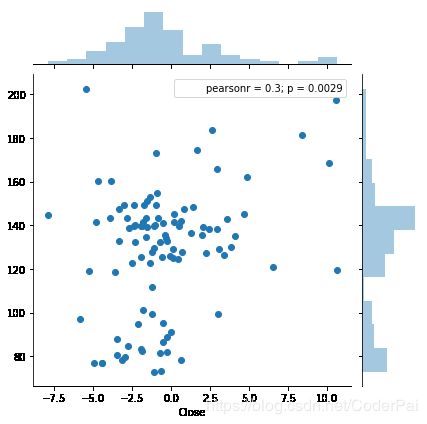
现在让我们将残差绘制到我们的预测中。
sns.jointplot(residuals,predictions)
plt.show()
让我们花一点时间来激烈我们到目前为止所涵盖的内容。我们手心使用定量或者数字和定性或者分类数据来创建我们的功能。我们将数据分为 80% 的训练和 20% 的测试。我们将模型与我们的数据进行拟合,然后通过传入我们的 X_test 集或我们的模型尚未看到的特征来使用它来进行预测。然后我们评估了我们的模型计算我们的 R-Squared 和我们的误差。
我们通过计算 y_test 和我们的预测之间的差异来计算残差或者误差。线性回归的关键假设是线性。这意味着该模型假设尽管我们的 x 值发生了变化,但斜率保持不变。为了检验这个假设,我们可以绘制残差的分布图。如果我们的残差是正太分布的,那么这意味着我们的线性假设是正确的。
我们还将残差绘制到我们的预测中。这是测试我们的线性数据的另一种方法。在简单线性回归中,我们可以将残差绘制为 X 或者预测变量。在这里,因为我们有多个预测变量,所以我们将残差或者误差绘制到我们的预测中。
当我们绘制残差的分布时,它们似乎不是正太分布的。此外,从查看残差图到我们的预测,我们可以看到我们的数据并不完全是线性的。这意味着我们可以通过使用非线性模型来改进模型并减少错误。我们可以通过引入多项式回归来实现这一目标。
多项式回归
我们将使用多项式回归来转换我们的线性模型,以更好的拟合非线性数据。
你可能想知道为什么它被称为多项式回归。这个方法之所以如此命名,是因为我们将线性方程转换为多项式方程。在我们的 PNB 示例中,我们有四个特征,所以我们的线性方程如下:
y = 6.08 + 0.93 x 1 + 0.02 x 2 + 0.28 x 3 − 1.94 x 4 y = 6.08+0.93x_{1} + 0.02x_{2} + 0.28x_{3} - 1.94x_{4} y=6.08+0.93x1+0.02x2+0.28x3−1.94x4
我们可以通过调用 lm 模型上的 .coef_ 和 .intercept 方法来检索我们的 B 0 B_{0} B0 和 B 1 B_{1} B1 。
检查我们的 B 1 B_{1} B1 。
lm.coef_
array([ 0.93884112, 0.01779704, 0.32920755, -1.89167465])
检查我们的 B 0 B_{0} B0
lm.intercept_
6.059062589910425
我们将创建一个数据框,以便更好的可视化我们的系数。
coefficients=pd.DataFrame(lm.coef_,index=X_train.columns,columns=['Coefficients'])
coefficients
| Coefficients | |
|---|---|
| Lag 1 | 0.938841 |
| Lag 2 | 0.017797 |
| Higher High | 0.329208 |
| Lower Low | -1.891675 |
现在我们可以清楚的看到每个特征的 B 1 B_{1} B1 。让我们可视化我们的特征,以便我们了解我们想要转换哪些功能。
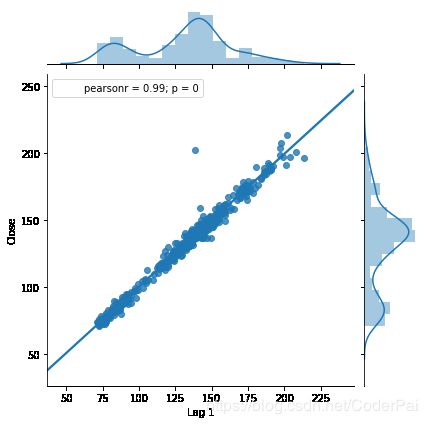
我们可以看到我们的 Lag 1 预测器具有更高系数。这表明它解释了我们的响应变量中大约 94% 的变化。让我们做一个回归图,以形成我们的 X 和 Y 变量之间的线性关系的基础。
sns.jointplot(PNB['Lag 1'], PNB['Close'], kind='regplot')
plt.show()
我们的 lower low 特征具有最低的 B1 值,让我们可视化它:
plt.figure(figsize=(10,6))
sns.boxplot(x='Lower Low',y='Close',hue='Lower Low',data=PNB)
plt.show()
我们可以看到 Lag 1 特征的系数与 Lag 2 特征之间的显著下降。让我们看看我们的 Lag 2 特征。
plt.figure(figsize=(10,6))
sns.lmplot('Lag 2', 'Close', data=PNB)
plt.show()
我们可以看到我们的 Lag 2 特征与 Lag 1 特征的匹配相差很大。这是我们想要关心的事情。我们的 Lag 1 特征的系数为 94%,而 Lag 2 特征的系数为 2%。这可以通过我们的数据与最佳拟合线的接近程度来看出。考虑到 Lag 1 和 Lag 2 之间的距离,这是一个显著的下降。我们还可以看到,在这两种情况下,我们都有远离我们数据和线的点。
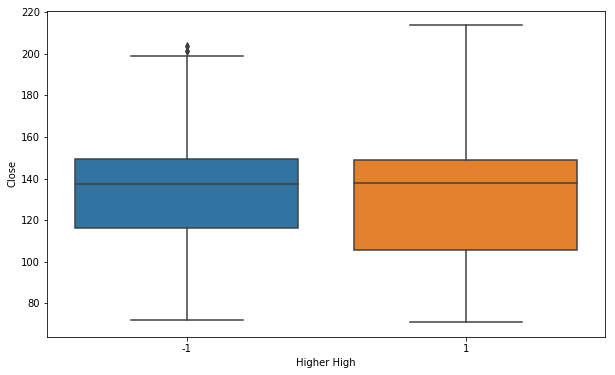
现在让我们看看我们的 Higher Highs 与 我们的收盘价。
plt.figure(figsize=(10,6))
sns.boxplot(x='Higher High',y='Close',data=PNB)
plt.show()
让我们改变我们的线性方程,以减少我们的均方误差。我们的模型看起来很适合我们的数据,可能是由于 Lag 1 和 Closing Price 之间的关系。但是,我们不一定能给予 Lag 1 所有的功劳,因为解释变量之间可能存在一些关系,这些关系可能会使他们与我们的回答的真实关系变得平静。这是线性模型的假设。
我们将改变我们的 Lag 2 变量,有点奇怪的是,Lag 2 系数与我们的 Lag 1差别很大。我们将重写我们的返程以包括 Lag 2 的平方并构建我们的模型,看看这是否会降低我们的 MSE。为实现这一点,我们将这个新变量添加到我们的数据帧中。
在添加新变量之前,让我们查看一下我们的 PNB 数据帧。
PNB.head()
| High | Low | Open | Close | Volume | Adj Close | Lag 1 | Lag 2 | Higher High | Lower Low | |
|---|---|---|---|---|---|---|---|---|---|---|
| Date | ||||||||||
| 2016-01-01 | 117.900002 | 115.500000 | 116.000000 | 117.599998 | 4070369 | 117.599998 | NaN | NaN | -1 | -1 |
| 2016-01-04 | 117.000000 | 112.500000 | 117.000000 | 112.800003 | 6341172 | 112.800003 | 117.599998 | NaN | -1 | 1 |
| 2016-01-05 | 113.349998 | 110.199997 | 113.000000 | 110.599998 | 7271156 | 110.599998 | 112.800003 | 117.599998 | -1 | 1 |
| 2016-01-06 | 111.800003 | 109.300003 | 110.949997 | 109.599998 | 5910731 | 109.599998 | 110.599998 | 112.800003 | -1 | 1 |
| 2016-01-07 | 108.449997 | 104.500000 | 108.099998 | 105.050003 | 7497260 | 105.050003 | 109.599998 | 110.599998 | -1 | 1 |
接下来,让我们添加 Lag 2 的平方变量。
PNB['Lag 2 Squared']=PNB['Lag 2']**2
PNB.head()
| High | Low | Open | Close | Volume | Adj Close | Lag 1 | Lag 2 | Higher High | Lower Low | Lag 2 Squared | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Date | |||||||||||
| 2016-01-01 | 117.900002 | 115.500000 | 116.000000 | 117.599998 | 4070369 | 117.599998 | NaN | NaN | -1 | -1 | NaN |
| 2016-01-04 | 117.000000 | 112.500000 | 117.000000 | 112.800003 | 6341172 | 112.800003 | 117.599998 | NaN | -1 | 1 | NaN |
| 2016-01-05 | 113.349998 | 110.199997 | 113.000000 | 110.599998 | 7271156 | 110.599998 | 112.800003 | 117.599998 | -1 | 1 | 13829.759641 |
| 2016-01-06 | 111.800003 | 109.300003 | 110.949997 | 109.599998 | 5910731 | 109.599998 | 110.599998 | 112.800003 | -1 | 1 | 12723.840688 |
| 2016-01-07 | 108.449997 | 104.500000 | 108.099998 | 105.050003 | 7497260 | 105.050003 | 109.599998 | 110.599998 | -1 | 1 | 12232.359662 |
好的,现在让我们重建我们的模型,看看我们是否能够减少我们的 MSE。
polynomial_model=LinearRegression()
我们重新设置我们的 X 和 y 变量。
#dropping all columns except our features and storing in X
X_2=PNB.drop(['Open','High','Low','Close','Adj Close','Volume','Lag 2'],axis=1)
#Initializing our Response
y_2=PNB['Close']
我们现在可以进行我们的数据切分了。
X_train_2, X_test_2, y_train_2, y_test_2=train_test_split(X_2,y_2,test_size=0.2,random_state=101)
现在我们有了训练数据和测试数据,我们可以使用它来拟合我们的模型并生成预测。
#fitting our model
polynomial_model.fit(X_train_2.fillna(0),y_train_2)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
我们刚刚将 polyomial_model 拟合到我们的训练数据中。现在让我们使用它来使用我们的测试数据进行预测。
predictions_2=polynomial_model.predict(X_test_2)
我们刚刚作出了预测,现在我们可以计算系数,残差和误差。让我们首先创建一个数据帧来保存多项式模型中的系数。
polynomial_df=pd.DataFrame(polynomial_model.coef_,index=X_train_2.columns,columns=['Polynomial Coefficients'])
现在让我们查看我们的多项式 df。
polynomial_df.head()
| Polynomial Coefficients | |
|---|---|
| Lag 1 | 0.712158 |
| Higher High | 0.798293 |
| Lower Low | -2.015106 |
| Lag 2 Squared | 0.000987 |
现在让我们创建我们的残差并绘制它们。然后我们将重新计算模型的指标。
sns.distplot(residuals_2,bins=100)
让我们计算我们的 MSE,MAE,RMSE 和 R-Squared。
回想一下,为了计算我们的 R-Squared,我们在 sklearn 中使用解释的方差分数。
R_Squared_2=metrics.explained_variance_score(y_test_2,predictions_2)
#printing the R-Squared of our polynomial model
print('Polynomial Model R-Squared:',R_Squared_2)
Polynomial Model R-Squared: 0.9885352017585385
现在让我们计算一下我们的误差。
#Calculating MSE
MSE_2=metrics.mean_squared_error(y_test_2,predictions_2)
#Calculating MAE
MAE_2=metrics.mean_absolute_error(y_test_2,predictions_2)
#Calculating RMSE
RMSE_2=np.sqrt(MSE_2)
#Printing out Errors
print('Polynomial MSE:',MSE_2)
print('Polynomial MAE:', MAE_2)
print('Polynomial RMSE:',RMSE_2)
Polynomial MSE: 10.28943678262987
Polynomial MAE: 2.4067176596789865
Polynomial RMSE: 3.207715196620465
好了,我们可以看到,我们已经实现了进一步减少误差,并且还改进了我们的 R-Squared。
现在,让我们编写 PNB 的多项式方程。
y = ( 0.000997 ) ( X 2 ) 2 + ( 0.709128 ) ( X 1 ] ) + ( 0.737462 ) ( X 3 ) + ( − 2.087720 ) ( X 4 ) + 20.37 y=(0.000997)(X_{2})^{2} + (0.709128)(X_{1]}) + (0.737462)(X_{3}) + (-2.087720)(X_{4}) + 20.37 y=(0.000997)(X2)2+(0.709128)(X1])+(0.737462)(X3)+(−2.087720)(X4)+20.37
来源:quantinsti