客户流失分析:使用Logistic回归预测风险客户
我们都知道线性回归例程非常简单易懂。如果它明确指出自变量的值增加1点,则因变量增加b个单位。
但是,在预测离散变量时 - 例如,客户是否会与服务提供商保持联系,或者是否会下雨 - 逻辑回归将会发挥作用。没有很多不同的值,结果只能是1或0。
在本文中,我们将学习如何在Excel中构建一个简单的客户流失模型,我们将使用Solver通过减少交叉熵误差来优化此模型。
在我们深入了解逻辑回归的细节之前,让我们理解为什么当我们必须基于线性回归的以下限制来预测离散结果时,线性回归不起作用:
-
线性回归假设每个变量之间存在线性关系。但是,如果与竞争对手相比,客户为特定服务支付的费用较低,则客户离开服务提供商的机会将呈指数级变化。
-
线性回归假设随着自变量的增加,概率成比例地增加。
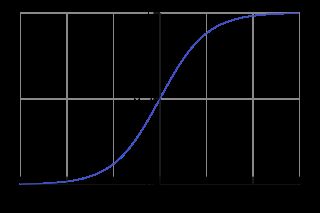
解决方案:Sigmoid曲线救援
如上所述,线性回归的主要问题是它假设变量之间存在线性关系,这在实践中非常罕见。
为了解决这个(以及其他一些)限制问题,我们将探索S形曲线。在外行人的语言中,我们可以说sigmoid函数(曲线)有助于返回概率值,然后可以将概率值映射到两个或更多个离散类。然而,一般来说,线性回归并不能告诉我们在某个范围之后事件发生的概率。
基于以上解释,我们可以说S形曲线可以比线性回归更好地解释离散现象。
为了简单起见,我将继续讨论本文的核心主题,即如何使用逻辑回归来留住客户。为此,我们将努力了解逻辑回归并了解如何实施。
众所周知,线性回归假设依赖变量和自变量之间存在线性关系。它表示为Y = x + b * X. Logistic回归通过应用S形曲线远离线性关系的概念。
上述符号清楚地表明逻辑回归如何使用自变量,这与线性回归相同。但是,同时,它还通过sigmoid激活将这些变量传递给0到1之间的输出。
现在,要看一下逻辑回归中输出如何变化,让我们借助一个例子来看一下逻辑回归方程的内幕:
-
如果X = 0,则Y = 1 /(1 + exp( - (2)))= 0.88
-
如果X增加2个单位(即X = 2),则Y的值为Y = 1 /(1 + exp( - (2 + 3 * 2)))= 1 /(1 + exp( - (( 5)))= 0.993
很明显Y的值从0.88变为0.99,因为X从0变为2.同样,如果X为-2,则Y将为0.017。因此,X中单位变化对Y的影响取决于等式。当X = 0时,值0.88可以解释为概率。例如,平均在88%的情况下,当X = 0时,Y的值为1。
物流回归在行动中
为了看到上面的等式和例程,我们将在Excel中运行构建逻辑回归方程。挑战在于能够根据下表中列出的一些变量来预测客户是否会与服务提供商保持联系。
要遵循的步骤
-
将自变量的权重初始化为随机值(假设各自为1)。
-
一旦权重和偏差被初始化,我们将通过对独立变量的多元线性回归应用S形激活来估计输出值(客户离开的概率= 1或停留= -0)。
下表包含有关sigmoid曲线的(a + b * X)部分和最终sigmoid激活值的信息:
获得上表中的数值的公式如下表所示:
前面的sigmoid激活col中的if条件。只是因为Excel在计算任何值> exp 500时有限制 - 因此裁剪。
误差估计
在线性回归中,我们考虑实际值和预测值之间的最小二乘(平方差)来估计总误差。在逻辑回归中,我们将使用称为交叉熵的不同误差度量。
交叉熵是两种不同分布之间差异的度量 - 实际和预测分布。
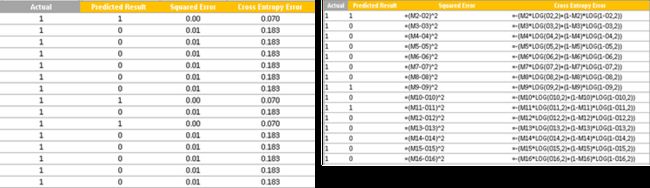
在因变量(Customer Churn)为1的情况下,让我们看一下两个成本函数(最小二乘法和熵成本):
上表清楚地表明,与平方误差相比,交叉熵方法对高预测误差进行了大量惩罚:较低的误差值在平方误差和交叉熵误差方面具有相似的损失,但是在存在高差异的情况下,交叉熵惩罚巨资。因此,在预测离散变量时,坚持使用交叉熵误差作为误差度量是一个好主意。
现在我们已经设置了问题,让我们改变参数,以减少整体错误。此步骤可以通过梯度下降来执行,这可以通过使用excel中的Solver功能来完成。
如何使用Solver执行逻辑回归?
注意:为了提高模型性能并减少错误,最好只引入具有统计意义的变量。对于此活动,可以遵循超出本文范围的不同方法。