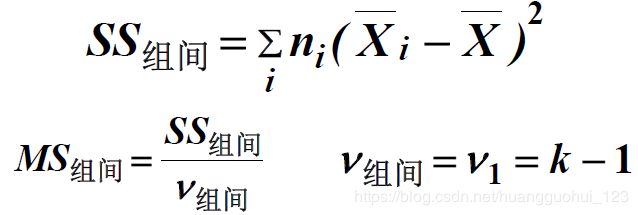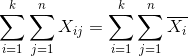统计推断——假设检验——方差分析
一、概述
方差分析（analysis of variance， ANOVA）用于两个或两个以上样本均数的比较，还可分析两个或多个研究因素的交互作用以及回归方程的线性假设检验等。
注意：方差分析常用于两个及两个以上独立样本均数的比较，当用于两个均数的比较时，同一资料所得结果与
检验等价，且有如下关系：
。
证明：
对于另个独立样本的的均值比较来说：
，
，
分子是组间的变异，分母是组内的变异之和。
基本思想：把全部观察值间的变异 —— 总变异按设计和需要分解成两个或多个组成部分，再比较每个部分的平均变异（均方）。
二、方差分析的基本思想
首先将总变异（
总）分解为组间变异(组间 )也叫处理变异和组内变异(组内 )也叫误差变异，然后比较两者的平均变异
组间 和组内 ，比较时采用两者的比值
值，即：
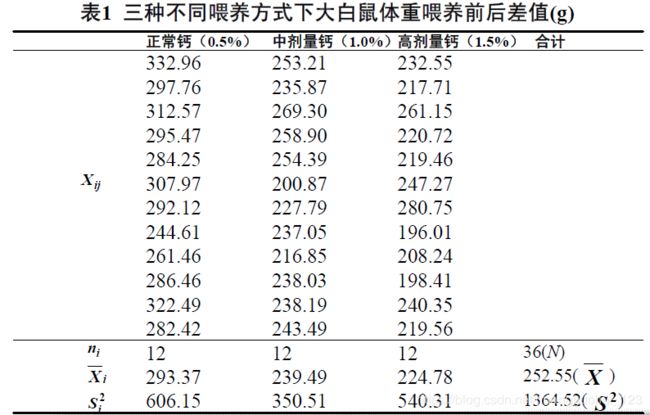
例 为研究钙离子对体重的影响作用，某研究者将36只肥胖模型大白鼠随机等分为三组，每组12只，分别给予高脂正常剂量钙(0.5%)、高脂中剂量钙(1.0%)和高脂高剂量钙(1.5%)三种不同的饲料，喂养9周，测其喂养前后体重的差值。问三个组不同喂养方式下大白鼠体重的改变是否不同？
其中，
表示各组的方差，
表示总体的方差，详细见《方差、协方差、标准差（标准偏差/均方差）、标准误、均方误差、均方根误差(标准误差)的区别》中的样本方差的计算。
总变异：也叫总的离均差平方和，反映全部个体之间总的变异情况。
总=
总=
为总体36个样本的均数，
为总体的样本数（该题为36），表示总体的方差，总为36个样本与总体均数的差异之和。
引起数据差异的原因有如下两个。
一是由于各组的水平不同，当假设
不真时，各个水平下指标的均值不同，这必然会使试验的结果不同，我们可以用组间变异来表示，如下。
组间变异：反映各组间均数的差异，即各组间均数与总的均数的差异，该变异除随机误差外，有可能存在处理因素的作用。
证明：方差分析算组间变异的时候为什么要乘以n？
设数据有
组，每组样本量为
，则总样本量为
。平方和的分解见下图
因为：
，中间一项消掉。
，对于每一个
来说，
都是相等的。
二是由于存在随机误差，即使在同一水平（同组）获得的数据，数据之间也有差异，这是除组间水平不同之外其他所有原因引起的，我们将他们归结为随机误差，可以用组内变异来表示，如下。
组内变异：也叫组内的离均差平方和，反映各组内个体间的差异，体现为每组的原始数据与该组均数的差异，因此可以认为是随机误差，又称误差变异，与处理因素没有关系。
为每组（3组，各12个样本）的均数，为组数，表示各组的方差，组内为36个样本与总体均数的差异之和。
如果各组的不同水平对结果没有影响（各组均值无差别），那么在组间误差中只包含随机误差，而没有系统误差。这时，组间误差与组内误差经过平均（F=MS组间/MS组内=[SS组间/(k-1)]/[SS组内/(N-k)]）后的数据就应该很接近，它们的比值就会接近1。反之，如果各组的不同水平对结果又影响（各组均值有所差别），那么组间误差除包含随机误差之外，还会包括系统误差，这时组间误差平均后的数值就会大于组内误差平均后的数值，它们之间的比值就会大于1.当这个比值大到某种程度时，就认为各组的不同水平之间存在显著差异，也就是自变量（控制自变量分成不同组）对因变量有显著影响。
方差分析的基本思想（二）
：
：至少有两个总体均数不相等
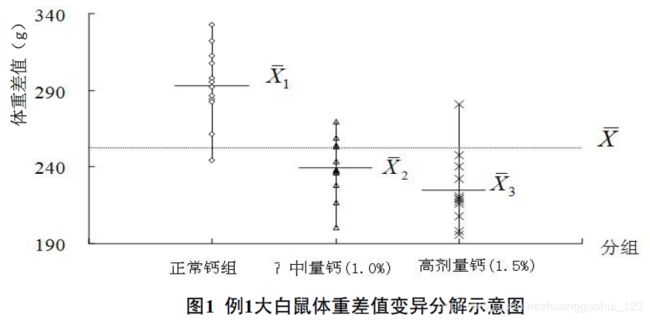
在本例中，若三组饲料的处理效应相同，则组间变异应与组内变异一样，只反映随机误差的作用大小。
如果三个总体均数相等，F 的数值不会太大（在1的左右不会太远）。相反，如果的数值过大，“三个总体均数相等”这个假设就值得怀疑了。
总离均差平方和分解为组间离均差平方和组内离均差平方和。
相应的总自由度分解为组间自由度和组内自由度。
证明：总=
=
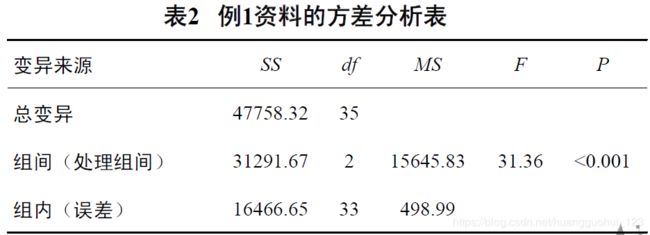
结合本例，将计算结果整理成如下的方差分析表。
表示离均差平方和，
表示自由度。
三、完全随机与随机区组设计资料的方差分析
1、完全随机设计（completely randomized design）
概述
是将同质的受试对象随机地分配到各处理组，再观察其实验效应。
完全随机设计是最常见的研究单因素两水平或多水平的实验设计方法，属单向方差分析(one-wayANOVA)。
完全随机设计资料方差分析的一般步骤
以上一节的例1为例
（1）建立检验假设，确定检验水准
：三组不同喂养方式下大白鼠体重改变的总体平均水平相同。
：三组不同喂养方式下大白鼠体重改变的总体平均水平不全相同。
（2）计算检验统计量
（3） 确定P值并作出推断结论
查F界值表，得 
，
。
由= 31.36 ，查表得到
< 0.001。按水准，差别有统计学意义，可以认为三组不同喂养方式下大白鼠体重改变的总体平均水平不全相同，即三个总体均数中至少有两个不等。
2、随机区组设计（randomized block design）
概述
又称配伍组设计，通常是将受试对象按性质(如动物的窝别、体重等非实验因素)相同或相近者组成
个区组(配伍组)，每个区组中的受试对象分别随机分配到
个处理组中去。
例2 为探索丹参对肢体缺血再灌注损伤的影响，将30只纯种新西兰实验用大白兔，按窝别相同分为10个区组。每个区组的3只大白兔随机接受三种不同的处理，即在松止血带前分别给予丹参2ml/kg、丹参1ml/kg、生理盐水2ml/kg，并分别测定松止血带前及松后1小时后血中白蛋白含量(g/L)，算出白蛋白的减少量如表2所示。问三种处理效果是否不同？
随机区组设计方差分析的总变异可以分为处理的变异、区组的变异和误差三部分。
随机区组设计资料方差分析的一般步骤
以例2为例
（1）建立检验假设，确定检验水准
对于处理组：
：三个处理组总体均数相等。
：三个处理组总体均数不全相等。
对于区组：
：十个区组总体均数相等。
：十个区组总体均数不全相等。
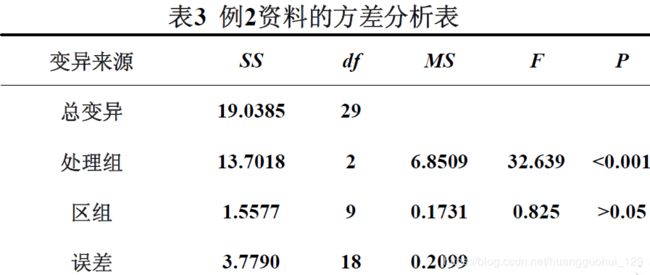
（2）计算检验统计量
（3）确定P值并作出推断结论
计算出处理和区组的值，并根据相应的自由度查界值表得出值。对于处理组， < 0.01，拒绝，可认为三种不同的处理效果不同，即三个总体均数中至少有两个不相同。对于区组，>0.05，不能拒绝，即尚不能认为十个区组的总体均数不同。
四、多个样本均数的两两比较
方差分析结果有统计学意义，则需要用两两比较的方法进一步确定哪些均数不相等；
1. 在研究设计阶段未预先考虑或预料到，经假设检验得出多个总体均数不全等的提示后，才决定进行多个均数的两两事后比较。这类情况常用于探索性研究，往往涉及到全部均数两两之间进行比较 ， 可采用 SNK(Students-Newman-Keuls)法、Bonferroni 法等。
2. 在设计阶段就根据研究目的或专业知识而计划好的某些均数间的两两比较。它常用于事先有明确假设的证实性研究，如多个处理组与对照组的比较，某一对或某几对在专业上有特殊意义的均数间的比较等，可采用Dunnett检验、LSD-t检验，也可用Bonferroni 法。
1、SNK法(又称q检验)：
属于多重极差检验，用于每两个均数间的比较。
例3 请对第二节例1资料喂养9周后体重差值的三组总体均数进行两两比较。
（1）建立检验假设，确定检验水准
：
，即两对比组的总体均数相等。
：
，即两对比组的总体均数不等。
（2）计算检验统计量：
首先将三个样本均数由大到小排列，并编组次：
注意：其中
误差=组内=498.99，自由度为误差的自由度
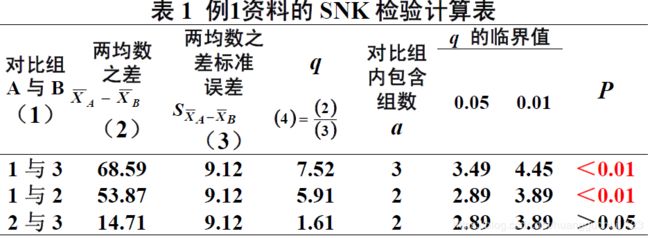
注意：对比组内包含组数a通俗理解为排列之后，对比组之间的步长，组1和组2的步长为2，组1和组3的步长为3。
（3） 确定P 值，下结论：
以组内自由度
组内 =33（本例取30）和对比组内包含组数 
查
界值表，得
和
的界值如表1所示。
按水准，组次 2 和 3（即中剂量钙 1.0%与高剂量钙 1.5%）不拒绝，差别无统计学意义，还不能认为这两种剂量钙喂养9周前后体重差值不同。其他两两组间均拒绝，差别有统计学意义，说明中、高剂量钙与正常钙喂养9周前后体重差值不同。
2、Bonferroni法：
属于调整
界值的方法。
若每次检验水准为
，共进行
次比较，若当为真时，犯第一类错误的累积概率
不超过
，也即
。此方法较为保守，检验功效低于SNK法，如果比较的次数过多（如大于10次），则一般不用Bonferroni法，因为检验功效太低。
例5 对例1资料，使用Bonferroni法对分别给予组1(高脂正常剂量钙0.5%)、组2(高脂中剂量钙1.0%)和组3(高脂高剂量钙1.5%)三种不同的饲料，喂养9周后体重差值的三组总体均数进行两两比较。
（1） 建立检验假设，确定检验水准
：，即两对比组的总体均数相等。
：，即两对比组的总体均数不等。
（2）计算检验统计量：
（3） 确定P 值，下结论：
按照
的水准，组2与组3差别无统计学意义，其他两两组间差别有统计学意义。
3、Dunnett法：
又称Dunnett–t 检验，适用于–1个实验组与对照组均数的比较。
例4 对第二节例2资料，问两种不同剂量丹参浓度分别与生理盐水对照组比较其总体均数是否不同？
（1）建立检验假设，确定检验水准
：
，即试验组与对照组的总体均数相等。
：
，即试验组与对照组的总体均数不等。
（2）计算检验统计量：
（3） 确定P 值，下结论：
根据自由度误差 =18，试验组数
(不含对照组）查Dunnett-t界值表。
按水准，丹参2ml/kg 与生理盐水组、丹参1ml/kg与生理盐水组均拒绝， 差别有统计学意义，可以认为两组试验组与对照组相比较大白兔血中白蛋白的减少量不同。
五、方差分析的前提条件和数据变换
1、方差分析的前提条件
理论上讲，进行方差分析的数据应满足如下两个基本假设：
(1) 各样本是相互独立的随机样本，均服从正态分布；
(2) 各样本的总体方差相等，即方差齐性。
2、方差分析的前提条件
Bartlett
检验：资料服从正态分布的多个总体方差齐性检验的方法 。
Levene检验：资料是任意分布时的方差齐性检验法，既可用于检验两总体方差齐性，也可用于检验多个总体的方差齐性。
3、方差齐性检验的基本步骤：（以例1为例）
（1）建立检验假设，确定检验水准
：
，即三个总体方差全相等。
：即三个总体方差不全相等。
（2）计算检验统计量：
（3） 确定P 值，下结论：
以自由度=2，查 界值表， 得0.50<<0.75。按= 0.1，不能拒绝 ，差异无统计学意义，尚不能认为三个总体方差不齐。
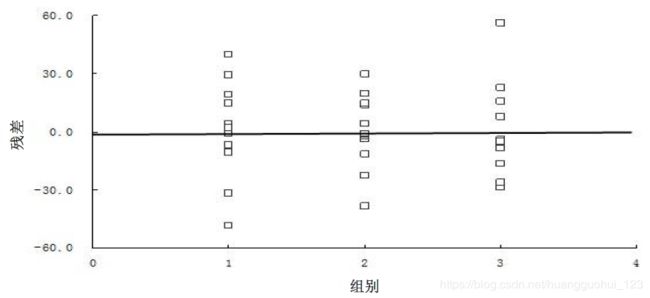
4、考察前提条件的残差图法
残差的计算公式：
完全随机设计资料：
随机区组设计资料：
5、数据变换
对于一些明显偏离正态性和方差齐性条件（不满足方差分析的前提条件）的资料，可以通过某种形式的数据变换使之满足方差分析、检验或其它统计方法对资料的要求。
所谓数据变换(data transformations)，即对原始数据作某种函数变换，它虽然改变了资料分布的形式，但未改变各组资料间的关系，其缺点是分析结果的解释欠直观。
常用的数据变换方法有：
1) 对数变换(logarithmic transformation) ：将原始数据取自然对数或常用对数。其变换公式为
，其中为零或正数。
该变换适用于：
(1)对数正态分布资料，如抗体滴度资料，疾病潜伏期等。
(2)标准差与均数成比例，或变异系数接近甚至等于某一常数的资料。
2) 平方根变换(square root transformation) ：将原始数据开算术平方根。
其变换公式为：
或
该变换适用于方差与均数成比例的资料，如服从Poisson分布的资料。
3) 平方根反正弦变换(arcsine square root transformation)：又称角度变换：就是将原始数据开平方根再取反正弦。
其变换公式为：
该变换适用于百分比的数据资料。
例如，
, 则变换为：