数据科学 案例6 逻辑回归2之 电信客户流失预警案例（代码）

8 逻辑回归

#subscriberID=“个人客户的ID”
#churn=“是否流失：1=流失”;
#Age=“年龄”
#incomeCode=“用户居住区域平均收入的代码”
#duration=“在网时长”
#peakMinAv=“统计期间内最高单月通话时长”
#peakMinDiff=“统计期间结束月份与开始月份相比通话时长增加数量”
#posTrend=“该用户通话时长是否呈现出上升态势：是=1”
#negTrend=“该用户通话时长是否呈现出下降态势：是=1”
#nrProm=“电话公司营销的数量”
#prom=“最近一个月是否被营销过：是=1”
#curPlan=“统计时间开始时套餐类型：1=最高通过200分钟；2=300分钟；3=350分钟；4=500分钟”
#avPlan=“统计期间内平均套餐类型”
#planChange=“统计结束时和开始时套餐的变化：正值代表套餐档次提升，负值代表下降，0代表不变”
#posPlanChange=“统计期间是否提高套餐：1=是”
#negPlanChange=“统计期间是否降低套餐：1=是”
#call_10086=“拨打10086的次数”

import os
import numpy as np
from scipy import stats
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt

1、导入数据和数据清洗

accepts = pd.read_csv(r'.\data\telecom_churn.csv',encoding='gbk')
accepts.head()

	subscriberID	churn	gender	AGE	edu_class	incomeCode	duration	feton	peakMinAv	peakMinDiff	posTrend	negTrend	nrProm	prom	curPlan	avgplan	planChange	posPlanChange	negPlanChange	call_10086
0	19164958.0	1.0	0.0	20.0	2.0	12.0	16.0	0.0	113.666667	-8.0	0.0	1.0	0.0	0.0	1.0	1.0	0.0	0.0	0.0	0.0
1	39244924.0	1.0	1.0	20.0	0.0	21.0	5.0	0.0	274.000000	-371.0	0.0	1.0	2.0	1.0	3.0	2.0	2.0	1.0	0.0	1.0
2	39578413.0	1.0	0.0	11.0	1.0	47.0	3.0	0.0	392.000000	-784.0	0.0	1.0	0.0	0.0	3.0	3.0	0.0	0.0	0.0	1.0
3	40992265.0	1.0	0.0	43.0	0.0	4.0	12.0	0.0	31.000000	-76.0	0.0	1.0	2.0	1.0	3.0	3.0	0.0	0.0	0.0	1.0
4	43061957.0	1.0	1.0	60.0	0.0	9.0	14.0	0.0	129.333333	-334.0	0.0	1.0	0.0	0.0	3.0	3.0	0.0	0.0	0.0	0.0

2、分类变量的相关关系

2.1 交叉表

#1两变量分析：检验该用户通话时长是否呈现出上升态势(posTrend)对流失(churn) 是否有预测价值
# ##  分类变量的相关关系
cross_table = pd.crosstab(accepts.posTrend,accepts.churn, margins=True)
#cross_table = pd.crosstab(accepts.bankruptcy_ind,accepts.bad_ind, margins=True)
cross_table

churn	0.0	1.0	All
posTrend
0.0	829	990	1819
1.0	1100	544	1644
All	1929	1534	3463

2.2 列联表

#法一：
def percConvert(ser):
    return ser/float(ser[-1])

cross_table = pd.crosstab(accepts.posTrend,accepts.churn, margins=True)
cross_table.apply(percConvert, axis=1)

churn	0.0	1.0	All
posTrend
0.0	0.455745	0.544255	1.0
1.0	0.669100	0.330900	1.0
All	0.557031	0.442969	1.0

print('''chisq = %6.4f 
p-value = %6.4f
dof = %i 
expected_freq = %s'''  %stats.chi2_contingency(cross_table.iloc[:2, :2]))

chisq = 158.4433 
p-value = 0.0000
dof = 1 
expected_freq = [[1013.24025411  805.75974589]
 [ 915.75974589  728.24025411]]

3、线性回归

3.1 数据预处理（字符型转化为数值型，查看变量间的关系）

# 中文乱码的处理
plt.rcParams['font.sans-serif'] = [u'SimHei']
plt.rcParams['axes.unicode_minus'] = False


accepts.plot(x = 'duration',y = 'churn', kind = 'scatter')
# plt.scatter(x=accepts2.age_oldest_tr, y=accepts2.bad_ind)

3.2 随机抽样，建立训练集与测试集

train = accepts.sample(frac=0.7, random_state=1234).copy()
test = accepts[~ accepts.index.isin(train.index)].copy()
print(' 训练集样本量: %i \n 测试集样本量: %i' %(len(train), len(test)))

 训练集样本量: 2424 
 测试集样本量: 1039

3.3 线性回归

lg = smf.glm('churn ~ duration', data=train, 
             family=sm.families.Binomial(sm.families.links.logit)).fit()  #逻辑回归，0-1分布（伯努利分布）
lg.summary()

Generalized Linear Model Regression Results

Dep. Variable:	churn	No. Observations:	2424
Model:	GLM	Df Residuals:	2422
Model Family:	Binomial	Df Model:	1
Link Function:	logit	Scale:	1.0000
Method:	IRLS	Log-Likelihood:	-1068.0
Date:	Thu, 20 Feb 2020	Deviance:	2136.0
Time:	10:35:15	Pearson chi2:	1.93e+03
No. Iterations:	7	Covariance Type:	nonrobust

	coef	std err	z	P>|z|	[0.025	0.975]
Intercept	2.5488	0.118	21.575	0.000	2.317	2.780
duration	-0.2422	0.011	-22.199	0.000	-0.264	-0.221

3.4 预测

train['proba'] = lg.predict(train)
test['proba'] = lg.predict(test)

test['proba'].head(10)

3     0.411422
5     0.591125
7     0.701216
8     0.792090
10    0.531554
12    0.531554
15    0.252598
16    0.860811
23    0.648136
26    0.003377
Name: proba, dtype: float64

3.5 模型评估

1、设定阈值

# 设定阈值

test['prediction'] = (test['proba'] > 0.5).astype('int')

2、混淆矩阵

pd.crosstab(test.churn, test.prediction, margins=True)

prediction	0	1	All
churn
0.0	427	156	583
1.0	88	368	456
All	515	524	1039

3、计算准确率

acc = sum(test['prediction'] == test['churn']) /np.float(len(test))
print('The accurancy is %.2f' %acc)

The accurancy is 0.77

#选取准确率最高的阈值
for i in np.arange(0.1, 0.9, 0.1):
    prediction = (test['proba'] > i).astype('int')
    confusion_matrix = pd.crosstab(prediction,test.churn,
                                   margins = True)
    precision = confusion_matrix.loc[0, 0] /confusion_matrix.loc['All', 0]
    recall = confusion_matrix.loc[0, 0] / confusion_matrix.loc[0, 'All']
    Specificity = confusion_matrix.loc[1, 1] /confusion_matrix.loc[1,'All']
    f1_score = 2 * (precision * recall) / (precision + recall)
    print('threshold: %s, precision: %.2f, recall:%.2f ,Specificity:%.2f , f1_score:%.2f'%(i, precision, recall, Specificity,f1_score))

threshold: 0.1, precision: 0.44, recall:0.97 ,Specificity:0.58 , f1_score:0.61
threshold: 0.2, precision: 0.53, recall:0.96 ,Specificity:0.62 , f1_score:0.69
threshold: 0.30000000000000004, precision: 0.59, recall:0.93 ,Specificity:0.64 , f1_score:0.72
threshold: 0.4, precision: 0.65, recall:0.89 ,Specificity:0.66 , f1_score:0.75
threshold: 0.5, precision: 0.73, recall:0.83 ,Specificity:0.70 , f1_score:0.78
threshold: 0.6, precision: 0.83, recall:0.77 ,Specificity:0.76 , f1_score:0.80
threshold: 0.7000000000000001, precision: 0.88, recall:0.75 ,Specificity:0.81 , f1_score:0.81
threshold: 0.8, precision: 1.00, recall:0.66 ,Specificity:1.00 , f1_score:0.79

4、绘制ROC曲线

import sklearn.metrics as metrics

fpr_test, tpr_test, th_test = metrics.roc_curve(test.churn, test.proba)
fpr_train, tpr_train, th_train = metrics.roc_curve(train.churn, train.proba)

plt.figure(figsize=[3, 3])
plt.plot(fpr_test, tpr_test, 'b--')
plt.plot(fpr_train, tpr_train, 'r-')
plt.title('ROC curve')
plt.show()
print('AUC = %.4f' %metrics.auc(fpr_test, tpr_test))

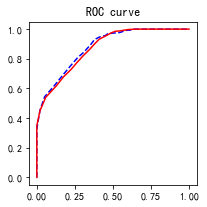
AUC = 0.8790

4、逻辑回归

4.1 包含分类预测变量的逻辑回归

# formula = '''churn ~ C(duration)'''

# lg_m = smf.glm(formula=formula, data=train, 
#              family=sm.families.Binomial(sm.families.links.logit)).fit()
# lg_m.summary()

4.2 多元逻辑回归

1、向前法

def forward_select(data, response):
    remaining = set(data.columns)
    remaining.remove(response)
    selected = []
    current_score, best_new_score = float('inf'), float('inf')
    while remaining:
        aic_with_candidates=[]
        for candidate in remaining:
            formula = "{} ~ {}".format(
                response,' + '.join(selected + [candidate]))
            aic = smf.glm(
                formula=formula, data=data, 
                family=sm.families.Binomial(sm.families.links.logit)
            ).fit().aic
            aic_with_candidates.append((aic, candidate))
        aic_with_candidates.sort(reverse=True)
        best_new_score, best_candidate=aic_with_candidates.pop()
        if current_score > best_new_score: 
            remaining.remove(best_candidate)
            selected.append(best_candidate)
            current_score = best_new_score
            print ('aic is {},continuing!'.format(current_score))
        else:        
            print ('forward selection over!')
            break
            
    formula = "{} ~ {} ".format(response,' + '.join(selected))
    print('final formula is {}'.format(formula))
    model = smf.glm(
        formula=formula, data=data, 
        family=sm.families.Binomial(sm.families.links.logit)
    ).fit()
    return(model)

#只有连续变量可以进行变量筛选，分类变量需要进行WOE转换才可以进行变量筛选

candidates = ['churn','duration','AGE','edu_class','posTrend','negTrend',\
              'nrProm','prom','curPlan','avgplan','planChange','incomeCode',\
              'feton','peakMinAv','peakMinDiff','call_10086']

data_for_select = train[candidates]

lg_m1 = forward_select(data=data_for_select, response='churn')
lg_m1.summary()

aic is 2139.9815513388403,continuing!
aic is 2015.2487668432518,continuing!
aic is 1950.666516634723,continuing!
aic is 1903.4002638032448,continuing!
aic is 1860.4602993108329,continuing!
aic is 1833.4423541609135,continuing!
aic is 1827.3343077471563,continuing!
aic is 1818.8478080369655,continuing!
aic is 1816.0480740672483,continuing!
aic is 1809.388996677547,continuing!
aic is 1806.4687346433138,continuing!
forward selection over!
final formula is churn ~ duration + feton + peakMinDiff + call_10086 + edu_class + AGE + prom + nrProm + posTrend + negTrend + peakMinAv 

Generalized Linear Model Regression Results

Dep. Variable:	churn	No. Observations:	2424
Model:	GLM	Df Residuals:	2412
Model Family:	Binomial	Df Model:	11
Link Function:	logit	Scale:	1.0000
Method:	IRLS	Log-Likelihood:	-891.23
Date:	Thu, 20 Feb 2020	Deviance:	1782.5
Time:	10:35:38	Pearson chi2:	1.93e+03
No. Iterations:	7	Covariance Type:	nonrobust

	coef	std err	z	P>|z|	[0.025	0.975]
Intercept	5.1489	0.456	11.298	0.000	4.256	6.042
duration	-0.2683	0.013	-20.387	0.000	-0.294	-0.242
feton	-1.2546	0.121	-10.367	0.000	-1.492	-1.017
peakMinDiff	-0.0024	0.000	-4.922	0.000	-0.003	-0.001
call_10086	-0.7969	0.120	-6.647	0.000	-1.032	-0.562
edu_class	0.4931	0.075	6.613	0.000	0.347	0.639
AGE	-0.0207	0.004	-4.720	0.000	-0.029	-0.012
prom	2.1936	0.660	3.326	0.001	0.901	3.486
nrProm	-0.6564	0.236	-2.776	0.006	-1.120	-0.193
posTrend	-1.5331	0.404	-3.797	0.000	-2.325	-0.742
negTrend	-1.2694	0.402	-3.161	0.002	-2.056	-0.482
peakMinAv	0.0010	0.000	2.203	0.028	0.000	0.002

2、计算方差膨胀因子

# Seemingly wrong when using 'statsmmodels.stats.outliers_influence.variance_inflation_factor'
#计算方差膨胀因子，若其> 10 表示某变量的多重共线性严重.
def vif(df, col_i):
    from statsmodels.formula.api import ols
    
    cols = list(df.columns)
    cols.remove(col_i)
    cols_noti = cols
    formula = col_i + '~' + '+'.join(cols_noti)
    r2 = ols(formula, df).fit().rsquared
    return 1. / (1. - r2)

exog = train[candidates].drop(['churn'], axis=1)

for i in exog.columns:
    print(i, '\t', vif(df=exog, col_i=i))
#posTrend,negTrend;curPlan,avgplan有明显的共线性问题,剔除其中两个后重新建模

duration 	 1.1649188214231452
AGE 	 1.060405955441583
edu_class 	 1.091937406580932
posTrend 	 10.87998721692619
negTrend 	 10.799093191856452
nrProm 	 10.594010492273254
prom 	 10.642709479318954
curPlan 	 228.06562536008082
avgplan 	 224.90961280080845
planChange 	 3.8781006983584954
incomeCode 	 1.0331700826612906
feton 	 1.032150079222362
peakMinAv 	 1.237319425737561
peakMinDiff 	 1.758824465225615
call_10086 	 1.027704090678157

3、岭回归和Lasso算法

（对最初的标准线性回归做一定的变化使原先无法求逆的矩阵变得非奇异，使得问题可以稳定求解。）

二分类：Logistic regression

多分类：Softmax分类函数

逻辑回归强烈推荐

#4）使用岭回归和Laso算法重建第三步中的模型，使用交叉验证法确定惩罚参数(C值)。并比较步骤四中Laso算法得到的模型和第三步得到的模型的差异
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
candidates = ['duration','AGE','edu_class','posTrend','negTrend','nrProm','prom','curPlan','avgplan','planChange','incomeCode','feton','peakMinAv','peakMinDiff','call_10086']
#data_for_select = churn[candidates]
scaler = StandardScaler()  # 标准化
X = scaler.fit_transform(accepts[candidates])
y = accepts['churn']

from sklearn import linear_model
from sklearn.svm import l1_min_c
# 构建“惩罚项”搜索空间，这里选择对数空间
cs = l1_min_c(X, y, loss='log') * np.logspace(0, 4)

print("Computing regularization path ...")
#start = datetime.now()
clf = linear_model.LogisticRegression(C=1.0, solver='liblinear',penalty='l1',tol=1e-6,max_iter =500)
coefs_ = []
for c in cs:
    clf.set_params(C=c)
    clf.fit(X, y)
    coefs_.append(clf.coef_.ravel().copy())
#print("This took ", datetime.now() - start)

coefs_ = np.array(coefs_)
plt.plot(np.log10(cs), coefs_)
ymin, ymax = plt.ylim()
plt.xlabel('log(C)')
plt.ylabel('Coefficients')
plt.title('Logistic Regression Path')
plt.axis('tight')
plt.show()

Computing regularization path ...

d:\Anaconda3\lib\site-packages\sklearn\svm\base.py:931: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
  "the number of iterations.", ConvergenceWarning)

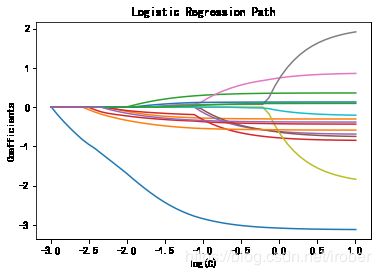
4、交叉验证

cs = l1_min_c(X, y, loss='log') * np.logspace(0, 4)
import matplotlib.pyplot as plt #可视化模块  
#将 cross_validation 改为 model_selection 即可
from sklearn.model_selection import cross_val_score # K折交叉验证模块  
#硬核消除警告
import warnings
warnings.filterwarnings("ignore")

k_scores = []  
clf = linear_model.LogisticRegression(penalty='l1')
#藉由迭代的方式来计算不同参数对模型的影响，并返回交叉验证后的平均准确率  
for c in cs:  
    clf.set_params(C=c)
    scores = cross_val_score(clf, X, y, cv=10, scoring='roc_auc')  #http://scikit-learn.org/stable/modules/model_evaluation.html
    k_scores.append([c,scores.mean(),scores.std()])  

5、可视化

data=pd.DataFrame(k_scores)#将字典转换成为数据框
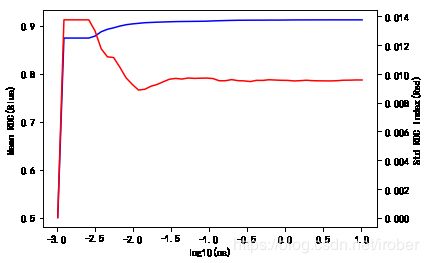
fig = plt.figure()

ax1 = fig.add_subplot(111)
ax1.plot(np.log10(data[0]), data[1],'b')
ax1.set_ylabel('Mean ROC(Blue)')
ax1.set_xlabel('log10(cs)')
ax2 = ax1.twinx()
ax2.plot(np.log10(data[0]), data[2],'r')
ax2.set_ylabel('Std ROC Index(Red)')

Text(0, 0.5, 'Std ROC Index(Red)')

5、合理的C

#得到合理的C为 np.exp(-1.9)
#重新实现Laso算法
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler

candidates = ['duration','AGE','edu_class','posTrend','negTrend','nrProm','prom','curPlan','avgplan','planChange','incomeCode','feton','peakMinAv','peakMinDiff','call_10086']
#data_for_select = churn[candidates]
scaler = StandardScaler()  # 标准化
X = scaler.fit_transform(accepts[candidates])
y = accepts['churn']

from sklearn import linear_model

clf = linear_model.LogisticRegression(C=np.exp(-1.9), penalty='l1')
clf.fit(X, y)
clf.coef_

array([[-2.91550192, -0.28678388,  0.31940015, -0.47182529, -0.29610763,
        -0.24445793,  0.33416986,  0.06622358,  0.        ,  0.        ,
         0.12293815, -0.5545222 ,  0.06489269, -0.3879872 , -0.35258674]])

5、KNN算法

from sklearn.neighbors import KNeighborsClassifier # K最近邻(kNN，k-NearestNeighbor)分类算法  
k_range = range(1, 40)  
  
k_scores = []  
  
#藉由迭代的方式来计算不同参数对模型的影响，并返回交叉验证后的平均准确率  
for k in k_range:  
    knn = KNeighborsClassifier(n_neighbors=k)  
    scores = cross_val_score(knn, X, y, cv=3, scoring='roc_auc')  
    k_scores.append([k,scores.mean(),scores.std()])  
#%%  
#可视化数据  
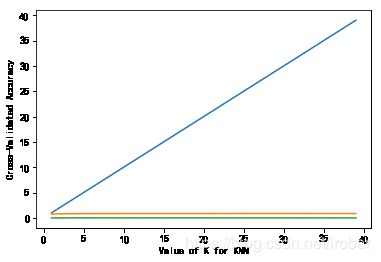
plt.plot(k_range, k_scores)  
plt.xlabel('Value of K for KNN')  
plt.ylabel('Cross-Validated Accuracy')  
plt.show()