【Codeforces Global Round 7】 A.B.C.D1.D2

Educational Codeforces Round 20

前言

好久没打cf的老年选手趁着早下班开了一场，感受到对于acm的某些思维有些淡忘了，但感觉这并不完全是坏事，只能说成绩与付出还是很有关系滴，以后尽量找时间再打打吧，不管打的怎么样，题解还是要写滴，只是补题很难有时间了~

A.Bad Ugly Number

题意

构造一个长度为n的数字X，要求X的每一位大于0而且X不是每一位的倍数。

做法

555555555555555558
由于558不是8的倍数，而且1000是8的倍数，所以这个数一定不是8的倍数~
做法估计有很多，用来做面试题估计效果不错~

B.Maximums

题意

给定长度为$n$($1\le n\le 10^5$)的$a$数组 $a_1,a_2,a_3...a_n$，
$b_1=0,b_2=max(b_1,a_1),b_3=max(b_2,a_2)....$
对于所有的$i$,$x_i=a_i-b_i$.

现在给出$x$数组，让你复原$a$数组。

做法

由于b数组是单调递增的而且$b_i$ 只与 $a_j(j<i)$有关，所以让$b_1=0$,之后可以得到$a_1$,之后可以得到$b_2$，依此类推，从前往后不断构造即可。

代码

#include
using namespace std;
const int maxn = 2e5+10;
int a[maxn];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    int mx=0;
    for(int i=1;i<=n;i++)
    {
        int res = a[i] + mx;
        mx = max(res,mx);
        printf("%d ",res);
    }
    return 0;
}

C.Permutation Partitions

题意

给你一个长度为$n(1\le n\le 2\ast 10^5)$的排列，现在要把整个排列划分成k段，每段的val为这段中的最大值，现在想让所有val的和最大，问最大值和方案数，注意方案数可能很大，要对998244353取模。

做法

很显然答案一定是最大的k个数相加，那么方案数呢？
设在答案中的数为Ans,那么很显然相邻的两个Ans一定不在同一个组，那么他们之间就可以产生一个分界线，分界线以左归左边的组，分界线以右归右面的组，而分界线的选择方案数就是两者的下标差，而对于每两个分界线，方案数应该是相乘的，所以最终把所有方案数相乘就是答案。

代码

#include
using namespace std;
typedef long long ll;
const int maxn = 2e5+10;
const int Mod = 998244353;
ll a[maxn];
int main()
{
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
    ll ans=0,cnt=1;
    for(int i=n;i>=n-k+1;i--) ans+=i;
    int pre=-1;
    for(int i=1;i<=n;i++)
    {
        if(a[i]>=n-k+1)
        {
            if(pre==-1) 
            {
                pre=i;
            }
            else
            {
                cnt = 1LL*cnt*(i-pre)%Mod;
                pre=i;
            }
        }
    }
    printf("%lld %lld",ans,cnt);
    return 0;
}

D.Prefix-Suffix Palindrome

题意

给出一个字符串s,找出一个最长的字符串t满足。
t是由s的前缀(可能为空)和s的后缀(可能为空)拼接而成的，而且t是一个回文串。

做法

首先考虑一个问题，会不会有这种情况。

红色区域表示前后相等的区域，而蓝色区域表示答案。
首先要考虑清楚，这种情况是否存在，也就是说舍弃两端相同的字符，只保留某一端的回文串，仔细思考可以发现，这种情况下，两个绿框也是回文的。

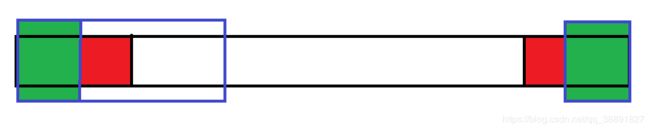
而且三个紫框(长度为1) 中的字符也是相同的。

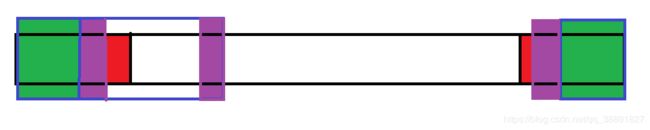
所以上述方案等价于：

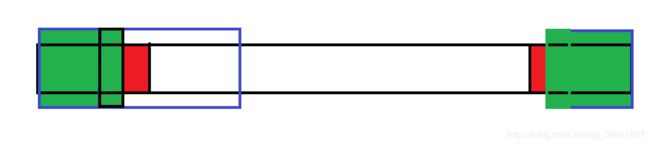
依次类推，可以把两端相同的元素都成对的去掉，那么只剩下中间一段字符串，我们分别求出前缀最长回文串和后缀最长回文串，取max即可,这里我用的是回文自动机PAM实现的，当然也可以用manacher。

代码

#include
using namespace std;
const int N=1e6+5,Max=26;
//记录一个以i为下标结尾得最长的字符串的长度
struct PAM{
    int nex[N][26],fail[N],s[N],len[N],ans[N],las,tot,n;
    int newnode(int le){
        for(int i=0;i<Max;++i) nex[tot][i]=0;
        len[tot]=le;
        return tot++;
    }
    void init(){
        tot=0,newnode(0),newnode(-1);
        n=las=0,s[0]=-1,fail[0]=1;
    }
    int get_fail(int x){
        while(s[n-len[x]-1]!=s[n]) x=fail[x];
        return x;
    }
    void add(int c,int pos){
        c-='a',s[++n]=c;
        int cur=get_fail(las);
        if(!nex[cur][c]){
            int now=newnode(len[cur]+2);
            fail[now]=nex[get_fail(fail[cur])][c];
            nex[cur][c]=now;
        }
        las=nex[cur][c],ans[pos]=len[las];//以pos这个位置的最长后缀回文串的长度为len[las]。
    }
}A;
int l[N],r[N];
char str[N];
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%s",str+1);int len=strlen(str+1);
        A.init();
        for(int i=1;i<=len;++i) A.add(str[i],i);//向左最长的后缀回文串
        for(int i=1;i<=len;i++) l[i]=A.ans[i];
        A.init();
        for(int i=len;i>=1;--i) A.add(str[i],i);//向右最长的前缀回文串(倒过来就是后缀回文串哦)
        for(int i=1;i<=len;i++) r[i]=A.ans[i];
        int ans=0;
        for(int i=1,j=len;i<=j && str[i]==str[j];i++,j--)
        {
            if(i==j) ans+=1;
            else ans+=2;
        }
        if(ans==len) cout<<str+1<<endl;
        else
        {
            if(r[ans/2+1]>l[len-ans/2])
            {
                for(int i=1;i<=ans/2;i++) printf("%c",str[i]);
                for(int i=ans/2+1;i<=ans/2+r[ans/2+1];i++) printf("%c",str[i]);
                for(int i=ans/2;i>=1;i--) printf("%c",str[i]);
            }
            else
            {
                for(int i=1;i<=ans/2;i++) printf("%c",str[i]);
                for(int i=len-ans/2-l[len-ans/2]+1;i<=len-ans/2;i++) printf("%c",str[i]);
                for(int i=ans/2;i>=1;i--) printf("%c",str[i]);
            }
            printf("\n");
        }
    }
}