Python数据分析实战之营销组合模型

营销组合模型概述

Marketing Mix Modeling （MMM）营销组合模型是一套统计分析技术，用来测量和预测不同营销行为对销售及ROI的影响。它被用来测量整体的marketing effectiveness并用来在不同的营销渠道中决定最优的预算分配

Marketing Mix中的“Mix”一词最早指的是Mix of 4Ps（Product，Price，Place & Promotion）。早期MMM分析的目的就是为了理解并找到这4P的最优组合，同时测量并预测不同的营销活动对销售的不同影响。

时至今日，MMM中包含的变量更加广泛，一个Marketing Mix Model可以由以下这些类型的数据组成：

• Target Audience data （目标用户数据）
• Product data （产品数据，包括产品价格、产品特征）
• Competitive data（竞品数据）
• Industry data（行业数据）
• Economic data（经济数据）
• Marketing data（营销数据）
• Conversion data（转化数据如sales，profit，ROI）

营销组合模型实战

1.首先导入数据与所需要的库

import pandas as pd
import numpy as np
import matplotlib.patches as mpatches
import matplotlib.pyplot as plt

data = pd.read_excel('MMM.xlsx')

2.EDA(探索性数据分析)

先大致的看一下各列数据

print (data.describe())

>>>         Brand ID         Year     Absolut  Aristocrat      Barton  \
count  263.000000   263.000000  263.000000  263.000000  263.000000   
mean    12.596958  2001.695817    0.049430    0.049430    0.049430   
std      7.654584     3.639093    0.217177    0.217177    0.217177   
min      1.000000  1995.000000    0.000000    0.000000    0.000000   
25%      6.000000  1999.000000    0.000000    0.000000    0.000000   
50%     12.000000  2002.000000    0.000000    0.000000    0.000000   
75%     18.000000  2005.000000    0.000000    0.000000    0.000000   
max     31.000000  2007.000000    1.000000    1.000000    1.000000   

        Belvedere     Burnett      Chopin  Crystal Palac   Finlandia  ...  \
count  263.000000  263.000000  263.000000     263.000000  263.000000  ...   
mean     0.026616    0.041825    0.026616       0.049430    0.049430  ...   
std      0.161265    0.200571    0.161265       0.217177    0.217177  ...   
min      0.000000    0.000000    0.000000       0.000000    0.000000  ...   
25%      0.000000    0.000000    0.000000       0.000000    0.000000  ...   
50%      0.000000    0.000000    0.000000       0.000000    0.000000  ...   
75%      0.000000    0.000000    0.000000       0.000000    0.000000  ...   
max      1.000000    1.000000    1.000000       1.000000    1.000000  ...   

       LagTotalMinusSales     TierSales  OutsideTierSales  LagTierSales  \
count          263.000000    263.000000        263.000000    263.000000   
mean         62673.935361   9547.235741      53106.615970   9215.528517   
std           1548.346560   2917.310122       2259.775837   2946.563257   
min          55687.000000    846.000000      48358.000000    697.000000   
25%          62459.000000   8151.500000      51863.000000   7493.000000   
50%          63204.000000  10605.000000      52335.000000  10400.000000   
75%          63616.000000  11209.000000      54570.000000  11127.500000   
max          64131.000000  15790.000000      59760.000000  14299.000000   

       LagOutsideTierSales  Firstintro  Marketshare  LagMktshare      YearID  \
count           263.000000  263.000000   263.000000   263.000000  263.000000   
mean          53458.406844    0.015209     0.046972     0.047470    9.695817   
std            2327.430916    0.122617     0.053831     0.054685    3.639093   
min           49806.000000    0.000000     0.001468     0.000971    3.000000   
25%           51947.000000    0.000000     0.014762     0.014655    7.000000   
50%           52419.000000    0.000000     0.029463     0.029181   10.000000   
75%           55392.000000    0.000000     0.053087     0.053633   13.000000   
max           59868.000000    1.000000     0.270477     0.270477   15.000000   

           total ad  
count    263.000000  
mean    7386.359312  
std    14280.852135  
min        6.000000  
25%        6.000000  
50%        6.000000  
75%     9691.400000  
max    70489.200000 

可以看出数据总共有263行，同时查看有没有缺失数据的存在。

#查看是否有空值
data.isnull().any()
                       ...  
diff                   False
IfDom                  False
DollarSales            False
PriceRerUnit           False
LagPrice                True
LnPrice                False
LnLPrice                True
Mag                    False
News                   False
                       ...  

查看列，数据的数据字典已经放在MMM数据文件中，可以对照着看一下各列的含义
注意：数据已经清洗过，所以缺失值较少，同时由于需要的字段中的数字数量级相差较大，所以对其进行取对数处理

print (data.columns)

>>>     [8 rows x 66 columns]
Index(['BrandName', 'Brand ID', 'Year', 'Absolut', 'Aristocrat', 'Barton',
       'Belvedere', 'Burnett', 'Chopin', 'Crystal Palac', 'Finlandia',
       'Fleischmann's', 'Fris', 'Gilbey's', 'Gordon's', 'Grey Goose',
       'Kamchatka', 'Ketel One', 'Level', 'McCormick', 'Polar Ice', 'Popov',
       'Pravda', 'Seagram's', 'Skol', 'Sky', 'Smirnoff', 'Stolicnaya',
       'Tanqueray', 'Three Olives', 'TotalSales', 'LagTotalSales',
       '2LagTotalSales', 'LnSales', 'LnLSales', 'Ln2Lsales', 'LnDiff', 'diff',
       'IfDom', 'DollarSales', 'PriceRerUnit', 'LagPrice', 'LnPrice',
       'LnLPrice', 'Mag', 'News', 'Outdoor', 'Broad', 'Print', 'LnMag',
       'LnNews', 'LnOut', 'LnBroad', 'LnPrint', 'Tier1', 'Tier2',
       'TotalMinusSales', 'LagTotalMinusSales', 'TierSales',
       'OutsideTierSales', 'LagTierSales', 'LagOutsideTierSales', 'Firstintro',
       'Marketshare', 'LagMktshare', 'YearID', 'total ad'],
      dtype='object')

接下来再看数据中一共有多少个品牌：

print (data['BrandName'].unique())
print ('\n')
print ('Total Number of brands',len(data['BrandName'].unique()))

>>>
['Absolut' 'Aristocrat' 'Barton' 'Belvedere' 'Burnett' 'Chopin'
 'Crystal Palac' 'Finlandia' "Fleischmann's" 'Fris' "Gilbey's" "Gordon's"
 'Grey Goose' 'Kamchatka' 'Ketel One' 'Level' 'McCormick' 'Polar Ice'
 'Popov' 'Pravda' "Seagram's" 'Skol' 'Sky' 'Smirnoff' 'Stolicnaya'
 'Tanqueray' 'Three Olives']


Total Number of brands 27

可以看到该数据集包括总共27个伏特加制造公司品牌。对于MMM，让我们选择一个品牌并分析价格对销售的影响。例如，让我们选择’Absolut’作为我们的分析品牌。

Absolut = data[data['BrandName'] == 'Absolut']]
Pr_Absolut = Absolut[['LnSales','LnPrice']]

之后画出Absolut的价格与销售之间的关系

plt.scatter(Pr_Absolut['LnPrice'],Pr_Absolut['LnSales'])
plt.xlabel('Log of Price')
plt.ylabel('Log of Sales')
plt.show()

matplotlib.pyplot.scatte函数的语法为：

matplotlib.pyplot.scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None, vmin=None, vmax=None, alpha=None, linewidths=None, verts=None, edgecolors=None, *, data=None, **kwargs)

参数的解释：
x，y：表示的是大小为(n,)的数组，也就是我们即将绘制散点图的数据点

s:是一个实数或者是一个数组大小为(n,)，这个是一个可选的参数。

c:表示的是颜色，也是一个可选项。默认是蓝色’b’,表示的是标记的颜色，或者可以是一个表示颜色的字符，或者是一个长度为n的表示颜色的序列等等，感觉还没用到过现在不解释了。但是c不可以是一个单独的RGB数字，也不可以是一个RGBA的序列。可以是他们的2维数组（只有一行）。

marker:表示的是标记的样式，默认的是’o’。

cmap:Colormap实体或者是一个colormap的名字，cmap仅仅当c是一个浮点数数组的时候才使用。如果没有申明就是image.cmap

norm:Normalize实体来将数据亮度转化到0-1之间，也是只有c是一个浮点数的数组的时候才使用。如果没有申明，就是默认为colors.Normalize。

vmin,vmax:实数，当norm存在的时候忽略。用来进行亮度数据的归一化。

alpha：实数，0-1之间。

linewidths:也就是标记点的长度

得到的散点图如下所示：

从生成的散点图中我们可以知道随着价格的增长销量增加。

import statsmodels.formula.api as sm
result = sm.ols(formula = 'LnSales ~ LnPrice',data = Pr_Absolut).fit()
result.summary()

Statsmodels 是 Python 中一个强大的统计分析包，包含了回归分析、时间序列分析、假设检
验等等的功能,当我们需要使用回归时，只需要import statsmodels.formula.api as sm即可（也可以import statsmodels.api as sm，两者的用法会有一些差别，但是具有相同的功能）。

使用sm.ols(formula = ‘LnSales ~ LnPrice’,data = Pr_Absolut).fit()即可获取拟合结果

#获取计算出的回归系数
print(result.params)

#打印出全部摘要
print(result.summary())

得到的回归系数与概要：

Intercept 2.836674
LnPrice 1.130972

从上述的描述中可以得到R方（R-squared）的值为0.688，即此函数接近69％的数据点。价格系数表明，每增加单位价格，销售额便增加1.13倍。同时P>|t|的值为0.表示两者之间有非常显著的关系

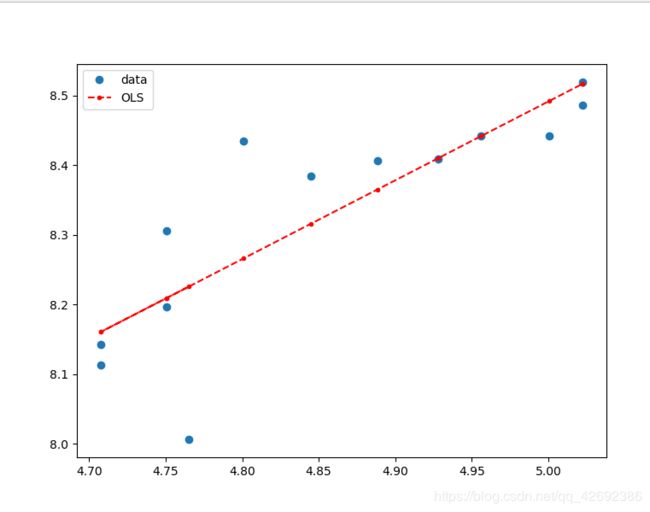
我们还可以将拟合结果画出来。

#先调用拟合结果的 fittedvalues 得到拟合的 y 值。
y_fitted = result.fittedvalues
#然后使用 matplotlib.pyploft 画图。首先设定图轴，图片大小为 8×6。
fig, ax = plt.subplots(figsize=(8,6))
#画出原数据，图像为圆点，默认颜色为蓝。
ax.plot(x, y, 'o', label='data')
#画出拟合数据，图像为红色带点间断线。
ax.plot(x, y_fitted, 'r--.',label='OLS')
#放置注解。
ax.legend(loc='best')

得到的拟合曲线与散点图的关系如图

接下来我们向回归中添加更多变量，看看R方会发生什么。

首先尝试使用广告和价格列

Ad_Absolut = Absolut[['LnSales','LnMag','LnNews','LnOut','LnBroad','LnPrint','LnPrice']]
result_ad = sm.ols('LnSales ~ LnMag + LnNews + LnOut + LnBroad + LnPrint + LnPrice',data=Ad_Absolut).fit()
result_ad.summary()

得到如下结果

调整R方值（Adj. R-squared）显示该模型能够解释87％的数据点。但是，此处某些变量的p值很高，这可能是由于相互作用效应和其他一些因素导致的。

• 注:多元回归实际应用中，判定系数R平方有个最大的问题：增加自变量的个数时，判定系数就会增加，即随着自变量的增多，R平方会越来越大，会显得回归模型精度很高，有较好的拟合效果。而实际上可能并非如此，有些自变量与因变量（即预测）完全不相关，增加这些自变量，并不会提升拟合水平和预测精度。调整R方同时考虑了样本量（n）和回归中自变量的个数（k）的影响，这使得调整R方永远小于R方，而且调整R方的值不会由于回归中自变量个数的增加而越来越接近1。因此，在多元回归分析中，通常用调整的多重判定系数来评价拟合效果

同时我们也可以通过其他的单因素的回归分析来判断各个媒体对实际销售的影响

通过回归系数，我们知道某一个自变量对自变量的影响的程度有多大

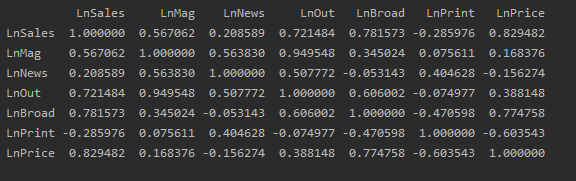
同时，我们还可以看一下各个因素与销售量之间相关性

print(Ad_Absolut.corr())

得到相关系数如图：

源码和实验数据文件可以关注公众号：Romi的杂货铺，回复"MMM"获取