重磅!深度学习圣经“花书”核心笔记、代码发布
点击上方“AI有道”,选择“置顶”公众号
重磅干货,第一时间送达![]()
《深度学习》,又名“花书”。该书由三位大佬 Ian Goodfellow、Yoshua Bengio 和 Aaron Courville 撰写,是深度学习领域奠基性的经典教材,被誉为深度学习的“圣经”。
原书内容非常充实,接近 800 页。这本书内容很深很全面,但起点稍微高了一些,对数学理论基础知识要求的比较多。因此,读完之后,及时进行高度概括和经验总结是十分有帮助的。石头君最近在 GitHub 上发现一个关于花书各章摘要的项目,内容非常精炼,除了笔记的同时,部分章节还配备代码,值得推荐,我们一起来看一下。
该项目的名称是:Deep-Learning-Book-Chapter-Summaries,作者是 Aman Dalmia 和 Ameya Godbole 两位小哥。项目地址为:
https://github.com/dalmia/Deep-Learning-Book-Chapter-Summaries
主要内容
这份花书核心笔记主要涉及的章节包括:
ch02 线性代数
ch03 概率与信息理论
ch04 数值优化
ch07 深度学习正则化
ch08 深度模型中的优化
ch09 卷积网络
ch11 实践方法论
ch13 线性因子模型
笔记的形式是 .ipynb,便于在 Jupyter Notebook 上打开和观看。例如,我们来看一下第二章线性代数的笔记。
可见,Jupyter 笔记不仅包含了知识点的总结,也有相关代码。再来看第九章的卷积网络部分,配备了一些完整的图片处理代码。
import numpy as np
from scipy import signal
from scipy import misc
import matplotlib.pyplot as plt
# %matplotlib inline
img = misc.ascent()
kernel = np.random.randn(5,5)
# kernel = np.array([[0,-10,0,10,0],[-10,-30,0,30,10],[0,-10,0,10,0]])
img = img.astype(np.float32)/255
orig_in = img
offsetx = offsety = 20
shift_in = np.zeros(orig_in.shape)
shift_in[offsetx:,offsety:] = img[:-offsetx,:-offsety]
rot_in = misc.imrotate(img, 90)
scale_in = misc.imresize(orig_in, 1.5)
output1 = signal.convolve2d(orig_in, kernel, mode='same')
output2 = signal.convolve2d(shift_in, kernel, mode='same')
output3 = signal.convolve2d(rot_in, kernel, mode='same')
output4 = signal.convolve2d(scale_in, kernel, mode='same')
fig, axes = plt.subplots(2, 4, figsize=(14, 7))
ax_orig = axes[0,0]
ax_shift = axes[0,1]
ax_rot = axes[0,2]
ax_scale = axes[0,3]
diff_orig = axes[1,0]
diff_shift = axes[1,1]
diff_rot = axes[1,2]
diff_scale = axes[1,3]
ax_orig.imshow(output1, cmap='gray')
ax_orig.set_title('Original')
ax_shift.imshow(output2, cmap='gray')
ax_shift.set_title('Shifted')
ax_rot.imshow(output3, cmap='gray')
ax_rot.set_title('Rotated')
ax_scale.imshow(output4, cmap='gray')
ax_scale.set_title('Scaled')
def shift(arr, offset):
output = np.zeros(arr.shape)
output[offset:, offset:] = arr[:-offset,:-offset]
return output
def rotate(arr, angle):
return misc.imrotate(arr, angle)
def resize(arr, scale):
return misc.imresize(arr, scale)
diff_orig.hist(np.ravel(output1),bins=100)
diff_orig.set_title('Output histogram')
diff_shift.hist(np.ravel(np.abs(output2-shift(output1, 20))),bins=100)
diff_shift.set_title('Shift histogram difference')
diff_rot.hist(np.ravel(np.abs(output3-rotate(output1, 10))),bins=100)
diff_rot.set_title('Rotate histogram difference')
diff_scale.hist(np.ravel(np.abs(output4-resize(output1, 1.5))),bins=100)
diff_scale.set_title('Scale histogram difference')
ax_orig.set_xticks([])
ax_shift.set_xticks([])
ax_rot.set_xticks([])
ax_scale.set_xticks([])
ax_orig.set_yticks([])
ax_shift.set_yticks([])
ax_rot.set_yticks([])
ax_scale.set_yticks([])
plt.tight_layout()
# plt.show()
plt.savefig('images/conv_equivariance.png')
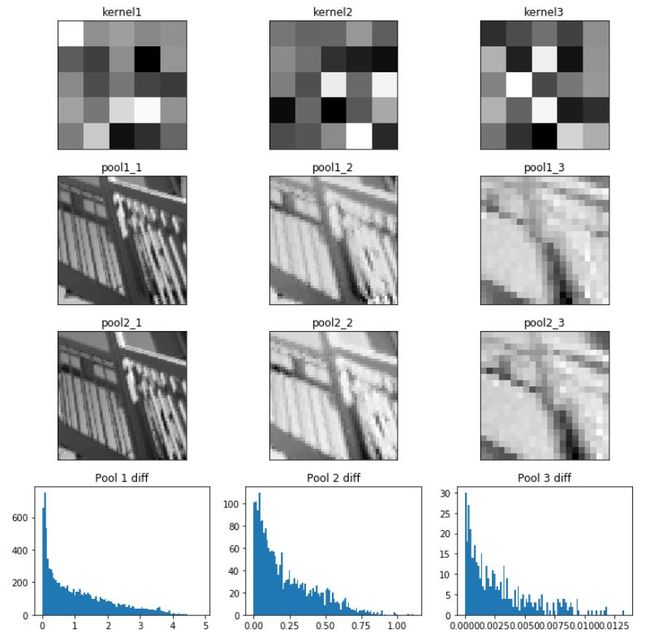
对于池化层的代码示例:
import numpy as np
np.random.seed(101)
from scipy import signal
from scipy import misc
import matplotlib.pyplot as plt
%matplotlib inline
img = misc.ascent()
img = img.astype(np.float32)/255
# The image is more interesting here
orig_in = img[-200:,-300:-100]
offsetx = offsety = 15
shift_in = img[-200-offsetx:-offsetx,-300-offsety:-100-offsety]
kernel1 = np.random.randn(5,5)
kernel2 = np.random.randn(5,5)
kernel3 = np.random.randn(5,5)
def sigmoid(arr):
# Lazy implementation of sigmoid activation
return 1./(1 + np.exp(-arr))
def maxpool(arr, poolsize, stride):
# Lazy looping implementation of maxpool
output_shape = np.floor((np.array(arr.shape)-poolsize)/stride)+1
output_shape = output_shape.astype(np.int32)
output = np.zeros(output_shape)
for x in range(output_shape[0]):
for y in range(output_shape[1]):
output[x,y] = np.max(arr[x*stride:x*stride+poolsize,y*stride:y*stride+poolsize])
return output
output1_1 = signal.convolve2d(orig_in, kernel1, mode='valid')
pool1_1 = maxpool(output1_1, 2, 2)
actv1_1 = sigmoid(pool1_1)
output1_2 = signal.convolve2d(actv1_1, kernel2, mode='valid')
pool1_2 = maxpool(output1_2, 2, 2)
actv1_2 = sigmoid(pool1_2)
output1_3 = signal.convolve2d(actv1_2, kernel3, mode='valid')
pool1_3 = maxpool(output1_3, 2, 2)
output2_1 = signal.convolve2d(shift_in, kernel1, mode='valid')
pool2_1 = maxpool(output2_1, 2, 2)
actv2_1 = sigmoid(pool2_1)
output2_2 = signal.convolve2d(actv2_1, kernel2, mode='valid')
pool2_2 = maxpool(output2_2, 2, 2)
actv2_2 = sigmoid(pool2_2)
output2_3 = signal.convolve2d(actv2_2, kernel3, mode='valid')
pool2_3 = maxpool(output2_3, 2, 2)
fig, axes = plt.subplots(4, 3, figsize=(10, 10))
k1, k2, k3 = axes[0,:]
p1_1, p1_2, p1_3 = axes[1,:]
p2_1, p2_2, p2_3 = axes[2,:]
h1, h2, h3 = axes[3,:]
k1.imshow(kernel1, cmap='gray')
k1.set_title('kernel1')
k2.imshow(kernel2, cmap='gray')
k2.set_title('kernel2')
k3.imshow(kernel3, cmap='gray')
k3.set_title('kernel3')
k1.set_xticks([])
k2.set_xticks([])
k3.set_xticks([])
k1.set_yticks([])
k2.set_yticks([])
k3.set_yticks([])
p1_1.imshow(pool1_1, cmap='gray')
p1_1.set_title('pool1_1')
p1_2.imshow(pool1_2, cmap='gray')
p1_2.set_title('pool1_2')
p1_3.imshow(pool1_3, cmap='gray')
p1_3.set_title('pool1_3')
p1_1.set_xticks([])
p1_2.set_xticks([])
p1_3.set_xticks([])
p1_1.set_yticks([])
p1_2.set_yticks([])
p1_3.set_yticks([])
p2_1.imshow(pool2_1, cmap='gray')
p2_1.set_title('pool2_1')
p2_2.imshow(pool2_2, cmap='gray')
p2_2.set_title('pool2_2')
p2_3.imshow(pool2_3, cmap='gray')
p2_3.set_title('pool2_3')
p2_1.set_xticks([])
p2_2.set_xticks([])
p2_3.set_xticks([])
p2_1.set_yticks([])
p2_2.set_yticks([])
p2_3.set_yticks([])
h1.hist(np.ravel(np.abs(pool1_1-pool2_1)),bins=100)
h1.set_title('Pool 1 diff')
h2.hist(np.ravel(np.abs(pool1_2-pool2_2)),bins=100)
h2.set_title('Pool 2 diff')
h3.hist(np.ravel(np.abs(pool1_3-pool2_3)),bins=100)
h3.set_title('Pool 3 diff')
plt.tight_layout()
# plt.show()
plt.savefig('images/pool_invariance.png')
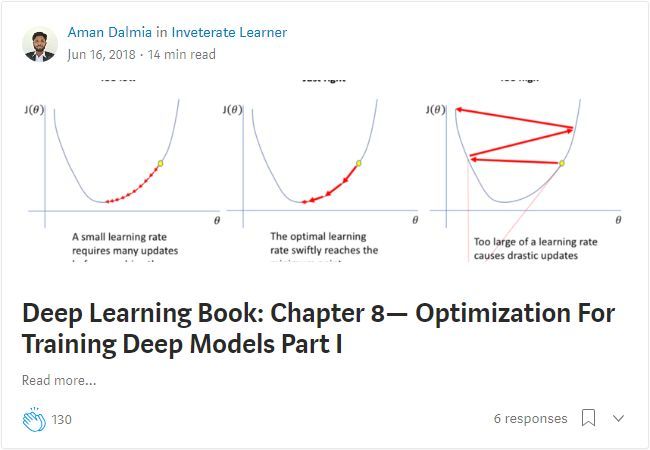
博客笔记
该项目的作者还在自己的个人网站上发布了花书的精炼笔记,地址为:
https://medium.com/inveterate-learner/tagged/deep-learning
附加资源
除了这份花书重点章节摘要之外,石头君还推荐一份来自 Microsoft 计算机软件工程师 Jeff Macaluso 总结的关于花书的经验法则!
在线版阅读地址:
https://jeffmacaluso.github.io/post/DeepLearningRulesOfThumb/
离线地址:
链接:
https://pan.baidu.com/s/1eLlJy3xB6Hs0w_Q7bO536g
提取码:7q1d
希望这份资源对你有所帮助~
【推荐阅读】
干货 | 公众号历史文章精选(附资源)
我的深度学习入门路线
我的机器学习入门路线图
![]()
?欢迎加入