吴恩达深度学习卷积神经网络学习笔记(1)

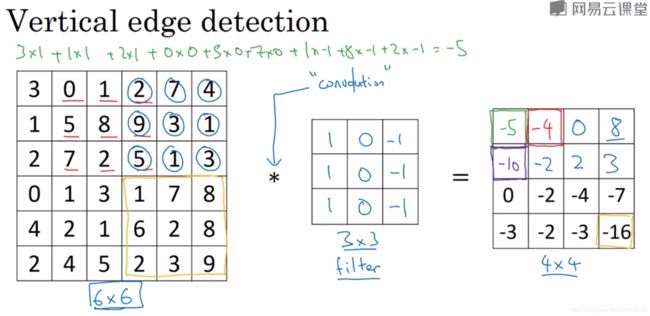
1垂直边缘检测器

图1.1

实现上图的卷积运算：

• python 中使用函数conv_forward
• 在tensorflow中使用函数tf.nn.conv2d
• 在keras框架中使用函数Conv2D

其实这个就是数字图像处理里图像分割里面的梯度算子。要得到一幅图像的梯度，要求在图像的每个像素处计算偏导数和。我们处理的是数字量，因此要求关于一点的领域上的偏导数的数字近似。

（1.1-1）

   (1.1-2)

这两个公式对所有x和y的有关值可用如图1.2所示的一维模板通过对的滤波来执行。

图1.2

左边实现公式（1.1-1）的一维模板，右边是实现公式（1.1-2）的一维模板。

在此基础上提出2x2大小的模版，但是它们对于用关于中心点对称的模版来计算边缘方向不是很有用，所以其最小模版大小为3x3。这些模板考虑了中心点对端数据的性质，并携带有关于边缘方向的更多信息。用大小为3x3的模板来近似偏导数的最简数字近似由下式给出：

（1.1-3）

（1.1-4）

这两个公式对应的模板称为Prewitt算子，如下图1.3所示。Prewitt算子实现比Sobel算子更简单，但是Sobel算子能够较好地抑制噪声，因为Sobel算子的模板中所有的系数之和为零，恒定灰度区域的响应为零。

 

图1.3

深度学习中的卷积层的过滤器与图像处理中的那些模板的区别在于，深度学习是通过学习去确定过滤器里面的参数，而图像处理中模版的参数一旦选择就确定了。

图像大小为X，过滤器大小为X，卷积层输出的大小为X。

2 填充（padding）

padding分为两种：

2.1.valid convalutions：

 X 

2.2.same convalutions：

 X 

 

3卷积步长（stride）

原图大小X，过滤器模板X，padding大小为，步长为，卷积层输出的大小为 X 

其中，表示向下取整。

 

4卷积和互相关

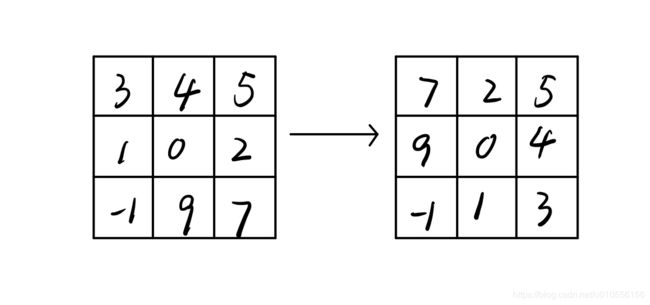
卷积在数学和信号处理中的定义与上面提到的卷积不同。例如一个过滤器，在进行卷积运算之前会进行翻转，如下图所示。

实际上我们之前做的被称之为互相关而不是卷积。但是按照深度学习和机器学习的惯例，我们将这个称为卷积运算。

 

在数学和信号处理中的卷积之所以需要翻转，是因为这种会带来结合律的性质：。在深度学习中不需要这个性质，所以省略了这个步骤。

 

5 多维矩阵

例如彩色图像就是三维矩阵，三个通道。过滤器的通道数（channel）必须和原图像的通道数相同。

XX * XX          卷积层输入大小 XX

不论输入的图片多大，卷积层的参数是固定的，这就是卷积神经网络的“避免过拟合”特征。

 

6 卷积层的一些标记方法（卷积标示法）

 filter size

 stride 步长

 padding 填充

 number of filter 通道数目

input：XX

output：XX

每一层过滤器的大小：XX

应用偏差和非线性函数之后，这一层的输出等于它的激活值    XX

当执行批量梯度下降，如果有m个例子，就是有m个激活值的集合，那么输出   X XX

如果采用批量梯度下降，变量的排列顺序如下：首先是索引和训练示例，然后是其他三个变量。

过滤器的权重（weight）就是所有过滤器的集合再乘以过滤器的总数目：XXX

损失数量L就是层中过滤器的个数。

偏差参数（bias）：     1X1X1X，偏差在代码中表示为一个1X1X1X的四维张量。

一个典型的卷积神经网络通常有三层：

• 一层是卷积层，我们通常用Conv来标注；
• 一个是池化层，称为为pool；
• 最后一个是全连接层（Fully connected），用FC表示。

7 池化层（pooling）

除了卷积层，卷积网路也是经常使用池化层来缩减模型的大小，提高计算速度，同时提高所提取特征的鲁棒性（robust）。

7.1 最大池化（Max Pooling）

池化的超级参数（hyperparameters包括：过滤器大小f，步幅s。常用数值f=2，s=2。使用最大池化很少用padding这个参数。

（注：里面有提高CAP特征，这个下来查一下资料）

最大化操作的功能就是只要在任何一个象限内提取到某个特征，它都会保留在最大池化的输出里。实际作用就是如果在过滤器中提取到某个特征，那么保留其最大值。如果没有提取到这个特征，可能在右上象限中不存在这个特征，那么其中的最大值也还是很小。

池化层虽然有超级参数，但是这些参数是不用学习的，一旦确定了f和s，它就是一个固定运算。执行反向传播（例如梯度下降）无需改变任何值。超级参数可以手动设置，也可以通过交叉验证设置。

上面提到的卷积层输入大小公式同样适用于池化层：

如果输入是xx(信道数目)，输出就是xx。个信道中的每个信道都单独执行最大池化计算。

7.2平均池化（Average pooling）

这个不太常用。

深度很深的神级网络，可以用平均池化来分解规模为7x7x1000的网络的表示层，在整个空间内求平均值，得到1x1x1000。但是在神经网络中最大池化还是比平均池化用的更多。

8 卷积神级网络示例

用类似LeNet-5这个神经网络模型来举例，许多参数选择都与LeNet-5类似。

人们在说神经网络有多少层的时候通常只是统计具有权重和参数的层，因为池化层没有权重和参数，只有超级参数，这里我们把Conv1和Pool1共同作为一个卷积，并标记为Layer1。

Layer2的输出5x5x16矩阵包含400个元素，将Pool2的输出平整化一个大小为400的一维向量。

池化层没有参数，卷积层参数相对较少，许多参数都是存在于神经网络的全连接层；随着神经网络的加深，激活值会逐渐变小，如果激活值下降的太快，会影响网络性能。

尽量不要自己设置超级参数，而是查看文献中别人采用了哪些超级参数。选一个在别人任务中效果很好的架构。

随着神经网络深度的加深，高度和宽度通常会减少，而信道数增加。

常见的神经网络模式：Conv（一个或者多个） Pool  Conv（一个或者多个） Pool  FC  FC  FC  softmax

 

9. 为什么使用卷积神经网络？

和只用全连接层相比，卷积层的两个主要优势在于：

• 参数共享；
• 稀疏链接。

卷积网络映射这么少参数有两个原因：1.参数共享。根据观察发现，特征检测如垂直边缘检测如果适用于图片的某个区域， 那么它也可能是适用于图片的其他区域；2.稀疏连接。如果过滤器是3x3，那么输出只依赖于3x3的输入单元，输出仅与输入特征中的9个相连接，而其他像素值都不会对输出产生任何影响。神经网络可以通过这两种机制减少参数，以便于我们用更小的训练集来训练它，从而预防过度拟合。

卷积神经网络善于捕捉平移不变。因为神经网络的卷积结构即使移动几个像素，这张图片依然具有非常相似的特征，应该属于同样的输出标记。实际上，我们在用同一个过滤器生成各层中图片的所有像素值，希望网络通过自动学习变得更加健壮，以便更好地取得所期望的平移不变属性。

例如要构建一个猫咪检测器，我们有下面这个标记训练集：表示一张图片，是二进制标记或某个重要标记。

卷积层和全连接层有不同的的参数w和偏差b，我们可以用任何参数集合来定义代价函数：

并随机初始化参数w和b，等于神经网络对整个训练集的预测的损失总和再除以m。使用梯度下降法（或者其他算法，例如含冲量的梯度下降、含RMSProp或者其他因子的梯度下降）训练网络来优化神经网络中的所有参数，以减少代价函数的值。