notice : 这篇文章仅仅具有上机实验的参考作用,并且需要配套的文件
_寄存器
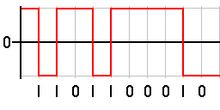
信号边缘
信号的一个 上升沿(rising edge) 是数字信号从低电平向高电平的转换;是下图的某些红色竖线
实践上高低电平的转变不是瞬间完成的,信号边缘不一定与时间轴垂直,有一定的延迟
rising edge-triggered
如果一个 触发器/Flip-flop/latch 忽略高电平转向低电平,只有当接入的时间脉冲信号从低电平向高电平转变(rising edge)才被触发;
这个触发器就被称为rising edge-triggered
下面介绍logisim中的寄存器
输入端:
| 使能Enable |
Enable=0时,使寄存器不能被时钟信号触发 |
| 时钟电路输入端 |
|
| 清空Reset |
Reset =1 时,寄存器值被清空 |
| 数据 |
被时钟触发时,储存到寄存器里的值 |
输出端
一个输出当前寄存器值的端口
电路时钟
能产生像时钟一样精确的震荡电路
_定点乘法运算
原码一位乘法
补码一位乘法
booth算法
假设有一个8位乘数multiplier:0111 1110,将产生6行非零的部分积;如果将multiplier记成1 0 0 0 0 0 -1 0 就可以大大减少非零行的数目
这种变换称为booth encoding,保证每两个连续位中最多只有一个是1或-1;这一变换把乘数变换成一个四进制形式
改进的booth encoding
编码如下
|
|
|
|
|
| 0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
X |
| 0 |
1 |
0 |
X |
| 0 |
1 |
1 |
2X |
| 1 |
0 |
0 |
-2X |
| 1 |
0 |
1 |
-X |
| 1 |
1 |
0 |
-X |
| 1 |
1 |
1 |
-0 |
所以 0111 1110 改写为01(1) 11(1) 11(1) 10(0) → 10(2Y) 00 00 -10(-2Y)
回过头来看经典的booth算法,如下图,是不是很简单
|
|
|
|
| 0 |
0 |
+0 |
| 0 |
1 |
+X |
| 1 |
0 |
-X |
| 1 |
1 |
+0 |
![]()
![]()
同时符号位增加一位,以便检验溢出(见课本)
部分积 0
部分积 0+00.1001
部分积 00.0010 01(>>2)
+11.0111
部分积 11.1001 01
部分积 11.1110 0101
+00.1001
=00.0111 0101
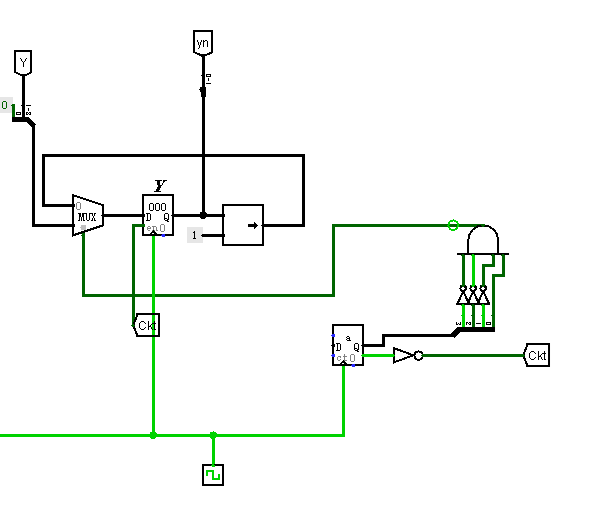
电路设计一位补码乘法器
输入被乘数X,与乘数Y
被乘数X符号位要增加一位
第8,9位是符号位
乘数Y后面要加一位0
然后把Y booth编码:
用yn表示y_(i+1)y_i
本文非常乱
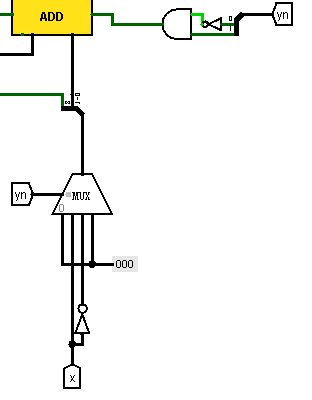
yn怎么产生呢?需要寄存器 {Memory}→Register
假设Y右移后的值是R(9位),存在一个寄存器里面
| auto R=bitset<9>(Y); iter_num=0; yn=bitset<2>(0b00); while(rising_edge){ iter_num++; if(iter_num==10) exit(0); elseif(iter_num==1) R=Y'; else R=R>>1; yn[0]=R[0]; yn[1]=R[1]; } |
iter_num可以用计数器实现 {Memory}→counter
隧道Ckt就是exit信号
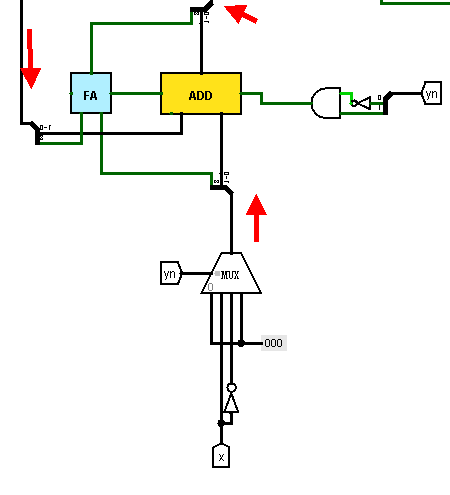
根据booth编码,求出 部分积PPi
如果 yn = 10 , 加法器还需要进位,才算求出-x的补码
部分积与之前累积的部分相加
红箭头标明了两个9位数之间的相加过程
剩下部分
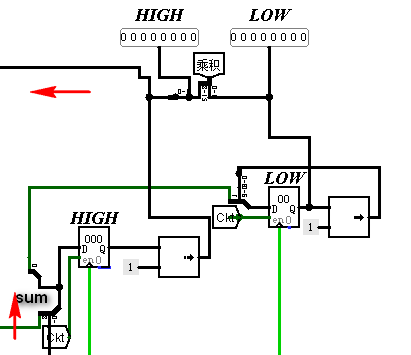
建两个寄存器,一个寄存器放乘积的高8位,一个放低8位,
目前为止出现的三个寄存器都用同一个时钟的上升沿触发,并用ckt隧道启动
每次求出的和(上图红箭头的输出部分:)记为S
S的最低位记作L
LOW寄存器存放的数记为Q
L作为最高位与(Q>>1)存入LOW寄存器,
![]()
S其余位存入HIGH寄存器,并右移作为下一次的被加数(上图左边的红箭头);