标准化和归一化，请勿混为一谈，透彻理解数据变换

1、标准化(Standardization)和归一化(Normalization)概念

1.1、定义

归一化和标准化都是对数据做变换的方式，将原始的一列数据转换到某个范围，或者某种形态，具体的：

归一化($Normalization$)：将一列数据变化到某个固定区间(范围)中，通常，这个区间是[0, 1]，广义的讲，可以是各种区间，比如映射到[0，1]一样可以继续映射到其他范围，图像中可能会映射到[0,255]，其他情况可能映射到[-1,1]；

标准化($Standardization$)：将数据变换为均值为0，标准差为1的分布切记，并非一定是正态的；

中心化：另外，还有一种处理叫做中心化，也叫零均值处理，就是将每个原始数据减去这些数据的均值。

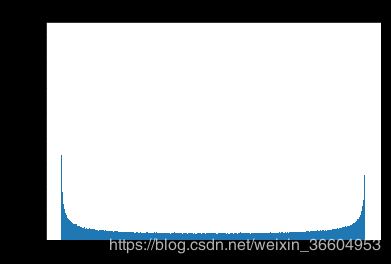
我在这里多写一点，很多博客甚至书中说，$Standardization$是改变数据分布，将其变换为服从$N(0,1)$的标准正态分布，这点是错的，Standardization会改变数据的均值、标准差都变了(当然，严格的说，均值和标准差变了，分布也是变了，但分布种类依然没变，原来是啥类型，现在就是啥类型)，但本质上的分布并不一定是标准正态，完全取决于原始数据是什么分布。我个举例子，我生成了100万个服从$beta(0.5,0.5)$的样本点(你可以替换成任意非正态分布，比如卡方等等，beta(1,1)是一个服从$U(0,1)$的均匀分布，所以我选了$beta(0.5,0.5)$)，称这个原始数据为$b_0$，分布如下图所示：

通过计算机计算，样本$b_0$的均值和方差分别为0.49982和0.12497(约为0.5和0.125)
对这个数据做$Standardization$，称这个标准化后的数据为$b_1$，分布如下：

可以看到数据形态完全不是正态分布，但是数学期望和方差已经变了。beta分布的数学期望为$\frac{a}{a+b}$，方差为$\frac{ab}{(a+b{)}^2(a+b+1)}$，所以$E(b_0)=\frac{0.5}{0.5+0.5}=\frac{1}{2}$，$Var(b_0)=\frac{1}{8}$，这也和我们上文所计算的样本均值和方差一致，而$b_1$的均值和方差分别为：-1.184190523417783e-1和1，均值和方差已经不再是0.5和0.125，分布改变，但绝不是一个正态分布，你不信的话，觉得看分布图不实锤，通过$qq$图和检验得到的结果如下：

你要的qqplot

你要的KS检验，拒绝正态性原假设。
当然，如果你原始数据就是正太的，那么做了$Standardization$，生成的就是标准正态的数据，切记哦，谁再和你说$Standardization$之后得到$N(0,1)$你就反驳他。
之所以大家会把标准化和正态分布联系起来，是因为实际数据中大部分都是正态分布，起码近似正态，另外，我看到很多人说标准化的基本假设是对正态数据，我并没有从哪些知名度较高的课本教材中查询到依据，如果有知道的同学也可以给我普及

1.2、联系和差异

一、联系

说完$Standardization$和$Normalization$的定义和通常的计算方式，再说说二者的联系和差异。
说道联系，$Standardization$和$Normalization$本质上都是对数据的线性变换，广义的说，你甚至可以认为他们是同一个母亲生下的双胞胎，为何而言，因为二者都是不会改变原始数据排列顺序的线性变换：
假设原始数据为$X$，令$\alpha =X_{max}-X_{min}$，令$\beta =X_{min}$(很明显，数据给定后$\alpha 、\beta$就是常数)，则$X_{Normalization}=\frac{X_i-\beta }{\alpha }=\frac{X_i}{\alpha }-\frac{\beta }{\alpha }=\frac{X_i}{\alpha }-c$，可见，$Normalization$是一个线性变换，按$\alpha$进行缩放，然后平移$c$个单位。其实$\frac{X_i-\beta }{\alpha }$中的$\beta$和$\alpha$就像是$Standardization$中的$\mu$和$\sigma$(数据给定后，$\mu$和$\sigma$也是常数)。线性变换，必不改变原始的排位顺序。

二、差异

1. 第一点：显而易见，$Normalization$会严格的限定变换后数据的范围，比如按之前最大最小值处理的$Normalization$，它的范围严格在$[0,1]$之间；
   而$Standardization$就没有严格的区间，变换后的数据没有范围，只是其均值是$0$，标准差为$1$。
2. 第二点：归一化($Normalization$)对数据的缩放比例仅仅和极值有关，就是说比如100个数，你除去极大值和极小值其他数据都更换掉，缩放比例$\alpha =X_{max}-X_{min}$是不变的；反观，对于标准化($Standardization$)而言，它的$\alpha =\sigma$，$\beta =\mu$，如果除去极大值和极小值其他数据都更换掉，那么均值和标准差大概率会改变，这时候，缩放比例自然也改变了。

1.3、标准化和归一化的多种方式

广义的说，标准化和归一化同为对数据的线性变化，所以我们没必要规定死，归一化就是必须到$[0,1]$之间，我到$[0,1]$之间之后再乘一个255你奈我何？常见的有以下几种：

1. 归一化的最通用模式$Normalization$，也称线性归一化(我看有些地方也叫rescaling，有待考证，如果大家看到这个词能想到对应的是归一化就行)：

$X_{new}=\frac{X_i-X_{min}}{X_{max}-X_{min}}$，范围[0,1]

2. Mean normalization：

$X_{new}=\frac{X_i-mean(X)}{X_{max}-X_{min}}$，范围[-1,1]

3. 标准化($Standardization$)，也叫标准差标准化：

$X_{new}=\frac{X_i-\mu }{\sigma }$，范围实数集

另外，我会在文章最后介绍一些比较常用的非线性数据处理方式比如boxcox变换等

2、标准化、归一化的原因、用途

为何统计模型、机器学习和深度学习任务中经常涉及到数据(特征)的标准化和归一化呢，我个人总结主要有以下几点，当然可能还有一些其他的作用，大家见解不同，我说的这些是通常情况下的原因和用途。

1. 统计建模中，如回归模型，自变量$X$的量纲不一致导致了回归系数无法直接解读或者错误解读；需要将$X$都处理到统一量纲下，这样才可比；
2. 机器学习任务和统计学任务中有很多地方要用到“距离”的计算，比如PCA，比如KNN，比如kmeans等等，假使算欧式距离，不同维度量纲不同可能会导致距离的计算依赖于量纲较大的那些特征而得到不合理的结果；
3. 参数估计时使用梯度下降，在使用梯度下降的方法求解最优化问题时， 归一化/标准化后可以加快梯度下降的求解速度，即提升模型的收敛速度。

3、什么时候Standardization，什么时候Normalization

我个人理解：如果你对处理后的数据范围有严格要求，那肯定是归一化，个人经验，标准化是ML中更通用的手段，如果你无从下手，可以直接使用标准化；如果数据不为稳定，存在极端的最大最小值，不要用归一化。在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，标准化表现更好；在不涉及距离度量、协方差计算的时候，可以使用归一化方法。
PS：PCA中标准化表现更好的原因可以参考(PCA标准化)

4、所有情况都应当Standardization或Normalization么

当原始数据不同维度特征的尺度(量纲)不一致时，需要标准化步骤对数据进行标准化或归一化处理，反之则不需要进行数据标准化。也不是所有的模型都需要做归一的，比如模型算法里面有没关于对距离的衡量，没有关于对变量间标准差的衡量。比如决策树，他采用算法里面没有涉及到任何和距离等有关的，所以在做决策树模型时，通常是不需要将变量做标准化的；另外，概率模型不需要归一化，因为它们不关心变量的值，而是关心变量的分布和变量之间的条件概率。

5、一些其他的数据变换方式

5.1、log变换

$X_{new}=lo{g}_{10}(X_i)/lo{g}_{10}(X_{max})$

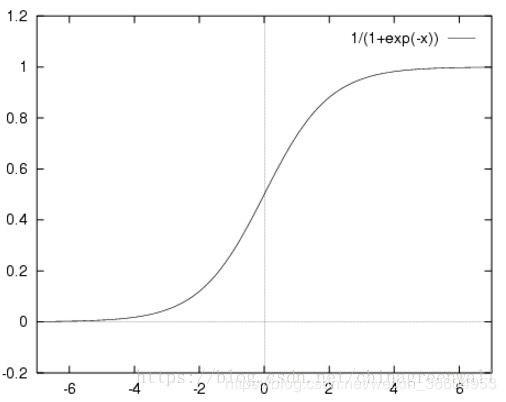
5.2、sigmoid变换(sigmoid函数)

$X_{new}=\frac{1}{1+e^{-X_i}}$

其图像如下：

5.3、softmax变换(softmax函数)

$X_{nex}=\frac{e^{X_i}}{\sum e^{X_i}}$

5.4、boxcox变换

下源自百度百科：

boxcox变换主要是降低数据的偏度，通常回归模型残差非正态或异方差的时候，会选择对y做boxcox变换，降低y的偏度，让y更接近正态。具体的，我以后如果写到回归或boxcox回归，和读者同学一起探讨。

6、结语

以上，及我个人对数据预处理中标准化和归一化的一些理解和说明。