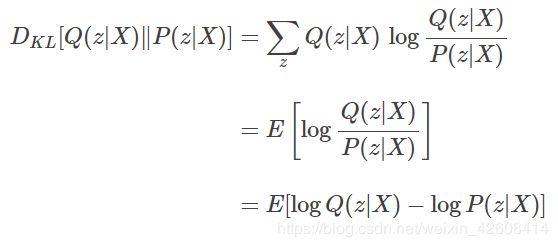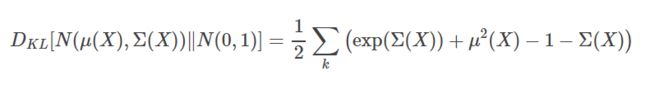使用VAE(变分自动编码器)，来预测用户流失.

原作者:Susan Li

原文来自Medium,略有增删。

变分自编码器（VAE）与生成对抗网络（GAN）一样，是无监督学习最具前景的方法之一，VAE类似于经典的自动编码器和是由一个编码器，一个解码器和一个损失函数构成的一个神经网络。它可以让我们设计复杂的数据生成模型，并使它们适合大型数据集。

在阅读有关使用卷积网络和自动编码器的文章后，我想VAE可以对有关用户流失问题的预测提供帮助，所以我决定将VAE应用于IBM样本数据集下载的电信流失数据中。将VAE应用于这样的相对较小的数据集有点过分，但为了学习VAE，我还是会这样做。

数据

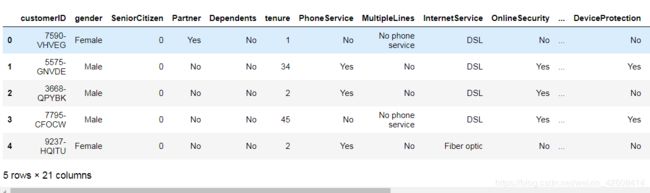
数据集中的每一行代表一个用户，每一列表示用户的属性,在这些属性中我们可能不太明白它的含义，不过这并不重要。

该数据集包括以下信息：

• Churn：目标变量,表示用户是否流失的标志
• 用户注册的服务如: phone, multiple lines, internet, online security, online backup, device protection, tech support, and streaming TV and movies.
• 客户帐户信息 - 他们成为客户的时长，合同，付款方式，无纸化帐单，每月费用和总费用
• 有关客户的人口统计信息 - 性别，年龄范围，以及是否有合作伙伴和家属。

import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler,MinMaxScaler
import collections
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import preprocessing
from sklearn.metrics import (confusion_matrix, precision_recall_curve, auc,
                             roc_curve, recall_score, classification_report, f1_score,
                             precision_recall_fscore_support, accuracy_score)
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler,MinMaxScaler
from keras.layers import Input, Dense, Lambda
from keras.models import Model
from keras.objectives import binary_crossentropy
from keras.callbacks import LearningRateScheduler
from keras.utils.vis_utils import model_to_dot
from keras.callbacks import EarlyStopping, ModelCheckpoint
import keras.backend as K
from keras.callbacks import Callback
import matplotlib
matplotlib.rcParams['figure.figsize'] = (10.0, 6.0)

df = pd.read_csv('./data/WA_Fn-UseC_-Telco-Customer-Churn.csv')
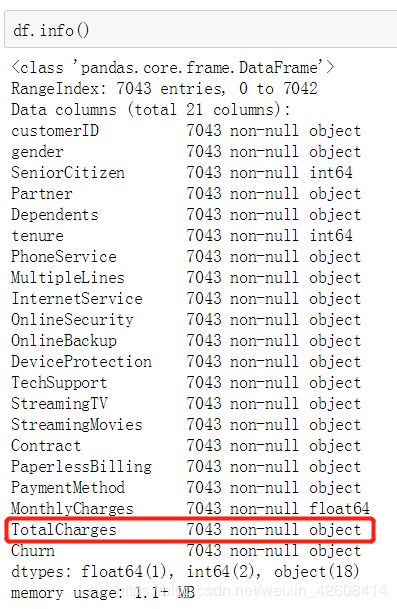
df.head()

接下来我们查看一下数据集中各个字段的信息： 

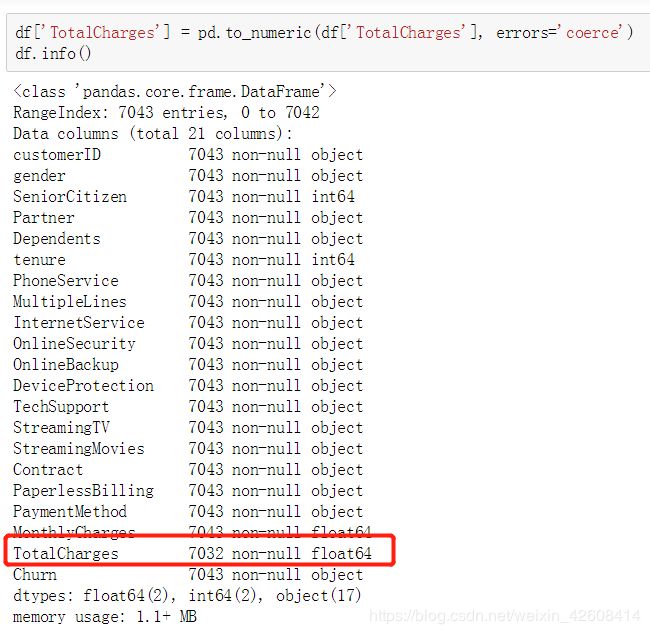
 我们看到大部分字段都是object，object表示为string型的分类型变量，其中TotalCharges表示为“总费用”,它应该是浮点型的，这里它被错误的定义为object的分类型变量，因此我们需要将其转换为float型的数值型变量:

 分类型变量的数据分析

接下来我们要对所有object类型的变量进行分析，我们想通过可视化的方式来观察它们与目标变量Churn之间是否存在某种关联关系

Gender(性别)

我们想查看性别字段和目标变量churn之间是否存在关联关系，是否存在特定性别的用户流失特别多的情况，我们通过画堆叠图的可视化方法,将两个性别的流失数量分别堆叠在性别数量的柱状分布图上，这个小技巧可以使我们同时对2个分类型变量进行交叉分析：

gender_plot = df.groupby(['gender', 'Churn']).size().reset_index().pivot(columns='Churn', index='gender', values=0)
print(gender_plot)
gender_plot.plot(x=gender_plot.index, kind='bar', stacked=True);
print('Gender', collections.Counter(df['gender']))

我们看到两个性别的用户流失数量非常接近，似乎性别对用户流失(churn)没有太多的关联关系。

Partner(伙伴)

接下来我们看一下Partner变量对用户流失的影响:

partner_plot = df.groupby(['Partner', 'Churn']).size().reset_index().pivot(columns='Churn', index='Partner', values=0)
partner_plot.plot(x=partner_plot.index, kind='bar', stacked=True);
print('Partner', collections.Counter(df['Partner']))

我看到 Partner变量有两个值yes和no，当Partner的值为no时流失数量是1200人，而当Partner的值为Yes时流失数量是699人,前者的流失数量接近后者流失数量的2倍，从上图中我们也可以很清晰的看到这一点，由此可见Partner和我们的目标变量Churn存在一定的关联关系。

phoneservice(电话服务)

接下来我们查看phoneservice与目标变量之间的关系

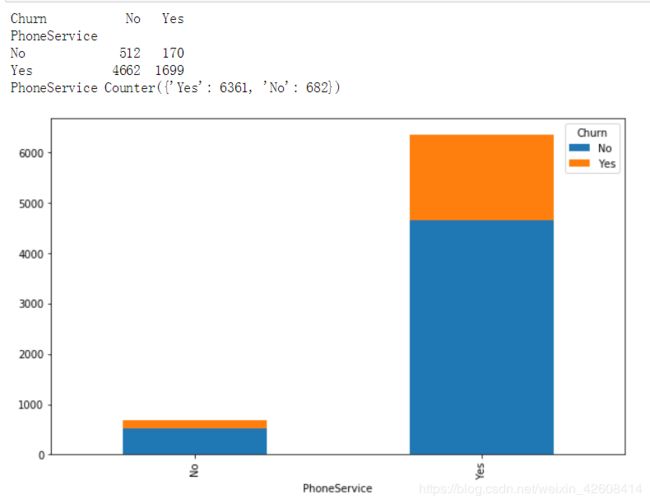
phoneservice_plot = df.groupby(['PhoneService', 'Churn']).size().reset_index().pivot(columns='Churn', index='PhoneService', values=0)
phoneservice_plot.plot(x=phoneservice_plot.index, kind='bar', stacked=True);
print(phoneservice_plot)
print('PhoneService', collections.Counter(df['PhoneService']))

 我们发现phoneservice包含两个值Yes和No,其中大部分的用户流失都发生在phoneservice为yes的时候。

MultipleLines

下面我们查看MultipleLines变量与目标变量的关系

multiplelines_plot = df.groupby(['MultipleLines', 'Churn']).size().reset_index().pivot(columns='Churn', index='MultipleLines', values=0)
multiplelines_plot.plot(x=multiplelines_plot.index, kind='bar', stacked=True);
print(multiplelines_plot)
print('MultipleLines', collections.Counter(df['MultipleLines']))

InternetService 

下面我继续查看InternetService变量与目标变量的关系

OnlineSecurity 

onlinesecurity_plot = df.groupby(['OnlineSecurity', 'Churn']).size().reset_index().pivot(columns='Churn', index='OnlineSecurity', values=0)
onlinesecurity_plot.plot(x=onlinesecurity_plot.index, kind='bar', stacked=True);
print(onlinesecurity_plot)
print('OnlineSecurity', collections.Counter(df['OnlineSecurity']))

OnlineBackup 

onlinebackup_plot = df.groupby(['OnlineBackup', 'Churn']).size().reset_index().pivot(columns='Churn', index='OnlineBackup', values=0)
onlinebackup_plot.plot(x=onlinebackup_plot.index, kind='bar', stacked=True);
print(onlinebackup_plot)
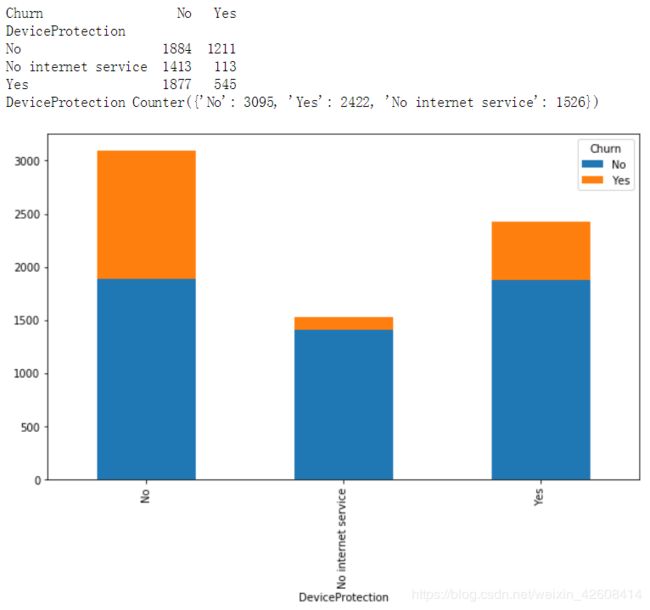
print('OnlineBackup', collections.Counter(df['OnlineBackup']))

DeviceProtection

deviceprotection_plot = df.groupby(['DeviceProtection', 'Churn']).size().reset_index().pivot(columns='Churn', index='DeviceProtection', values=0)
deviceprotection_plot.plot(x=deviceprotection_plot.index, kind='bar', stacked=True);
print(deviceprotection_plot)
print('DeviceProtection', collections.Counter(df['DeviceProtection']))

 

PaymentMethod 

paymentmethod_plot = df.groupby(['PaymentMethod', 'Churn']).size().reset_index().pivot(columns='Churn', index='PaymentMethod', values=0)
paymentmethod_plot.plot(x=paymentmethod_plot.index, kind='bar', stacked=True);
print(paymentmethod_plot)
print('PaymentMethod', collections.Counter(df['PaymentMethod']))

我们从上图中可以看到，当使用电子支票(Electronic check)时，用户的流失数量较多。

数值变量的分析 

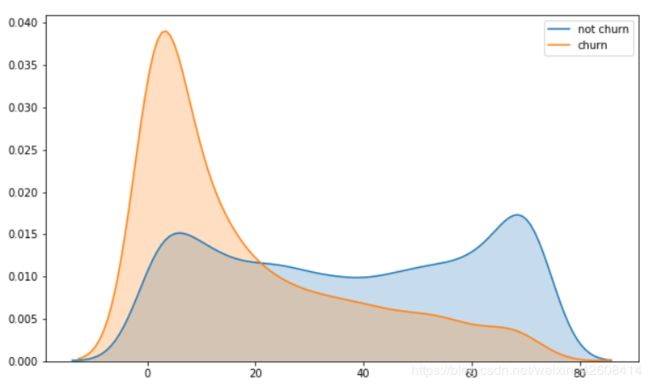
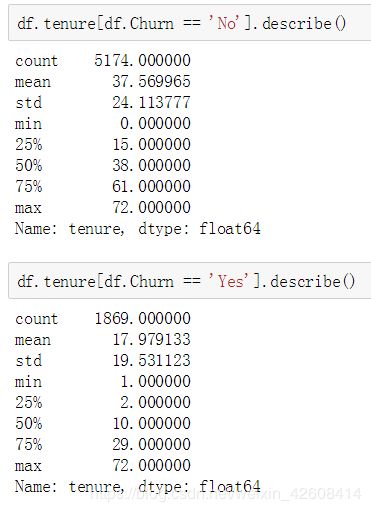
Tenure

接下来我们要查看Tenure变量的核密度图

sns.kdeplot(df['tenure'].loc[df['Churn'] == 'No'], label='not churn', shade=True);
sns.kdeplot(df['tenure'].loc[df['Churn'] == 'Yes'], label='churn', shade=True);

MonthlyCharges

 

sns.kdeplot(df.MonthlyCharges[df.Churn == 'No'], label='not churn', shade=True);
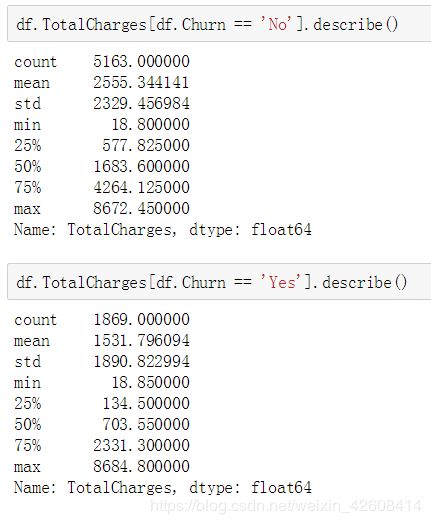
sns.kdeplot(df.MonthlyCharges[df.Churn == 'Yes'], label='churn', shade=True);

Total Charges 

sns.kdeplot(df['TotalCharges'].loc[df['Churn'] == 'No'], label='not churn', shade=True);
sns.kdeplot(df['TotalCharges'].loc[df['Churn'] == 'Yes'], label='churn', shade=True);

 数据预处理

对流失标志进行编码用0和1来代替No和Yes 

le = preprocessing.LabelEncoder()
df.Churn = le.fit_transform(df.Churn.values)

 用均值填充每一列的空值

df = df.fillna(df.mean())

对分类型变量进行one-hot编码

categorical =  ['gender', 'Partner', 'Dependents', 'PhoneService', 'MultipleLines', 'InternetService', 
                'OnlineSecurity', 'OnlineBackup', 'DeviceProtection', 'TechSupport', 'StreamingTV', 
                'StreamingMovies', 'Contract', 'PaperlessBilling', 'PaymentMethod']
for f in categorical:
    dummies = pd.get_dummies(df[f], prefix = f, prefix_sep = '_')
    df = pd.concat([df, dummies], axis = 1)
df.drop(categorical, axis = 1, inplace = True)

拆分数据(训练集、验证集、测试集)

X_train, X_val = train_test_split(df, test_size=2958)

cols = [c for c in df.columns if c not in ['customerID','Churn']]
y_train = X_train['Churn'].as_matrix()
X_train = MinMaxScaler().fit_transform(X_train[cols])
y_val= X_val['Churn'].as_matrix()
X_val = MinMaxScaler().fit_transform(X_val[cols])

X_val, X_test, y_val, y_test = train_test_split(X_val, y_val, test_size=1479, random_state=0)

def fit_batchsize(X,y,batch_size):
    n_size = (len(X)//batch_size)*batch_size
    X = X[0:n_size]
    y = y[0:n_size]
    return X, y

batch_size = 100

X_train, y_train = fit_batchsize(X_train,y_train, batch_size)
X_val, y_val = fit_batchsize(X_val, y_val, batch_size)

X_test,y_test = fit_batchsize(X_test,y_test, batch_size)

VAE(变分自动编码器)的解释

关于VAE大家可以参考这篇文章，当前有两种数据自动生成模型:生成性对抗网（GAN）和变分自动编码器（VAE）。这两种模型的差异在于他们训练模型的方式的不同。GAN是基于博弈论(game theory)，其目标是找到discriminator网络与generator 网络之间的纳什均衡(Nash Equilibrium)。而VAE是基于贝叶斯推理，即它想要模拟数据的基本概率分布，以便它可以从该分布中采样新数据。

我们的目标是是想通过前面分析的特征变量来预测用户流失的概率，经过前面的分析这些特征变量或多或少都与目标变量(Churn)存在关联关系，而这些关联关系并非直接的因果关系，这就好比吸引和肺癌之间的关系，大部分的肺癌患者都有吸烟的历史，吸烟似乎和肺癌之间存在较强的关联关系，但目前并不能认定吸烟和肺癌之间存在直接的因果关系即只要吸烟就会得肺癌。因为仍然有很多吸烟的人没有得肺癌。

使用VAE模型来分析用户流失预测的问题

联系到我们现在要解决的用户流失预测的问题，用VAE模型是这样来解释用户流失问题是这的：所有用户流失的数据都服从一个特定的分布，而这个特定的分布包含了一个我们还没有发现了的潜在变量z,正是这个潜变量z它决定了特定分布的形状和范围。假如我们能找到了这个潜变量z,那我们就知道了这个特定分布的形状和范围，那么只要遇到符合这个特定分布的特征变量(如Partner，phoneservice，MultipleLines等)，我们就可以认定用户会流失。因此我们的目标就是要找到这个潜变量z,并用这个潜变量z来生成用户流失数据的特定分布。我们做如下的定义:

• X: 表示我们当前的数据
• z: 潜变量(能够生成流失数据的特定分布)
• P(X): 当前数据的分布
• P(z): 潜变量的分布
• P(X|z): 用潜变量z生成用户流失的特定分布。

这里许说明一下，因为我们不知道潜变量z的具体数值，因此我们假定潜变量z其自身也服从某一分布记作P(z)，只是我们并不知道这个分布的具体参数。那么VAE的思想就是通过P(z|X)来推断出P(z)。但是我们并不知道P(z|X)的参数，无法确定P(z|X)的分布，此时VAE会使用一个简单的容易评估的分布记作Q(z|X)(如正太分布)来推断P(z|X)，并使用相对熵（KL divergence）来测量Q(z|X)和P(z|X)这两个分布之间的差异:

最后经过一系列的推导以后我们得到VAE的理论目标函数:

这里需要说明一下：

• Q(z|X): 用来推断P(z|X)的分布
• z: 潜变量
• P(X|z): 使用潜变量生成的用户流失数据的分布。

如果大家熟悉GAN的自动编码器(Autoencoder) 的话，很容易看出来其实Q (z|X )是编码器网络，z是编码的表示，P (X | z ）是解码器网络。

最后再经过一系列的推导以后，我们将理论目标损失函数相对熵（KL divergence）转换成可以实战的目标函数:

VAE在Keras中的实现

以下的代码来自于这篇博客，请大家仔细阅读。代码结构大致如下

• 定义输入图层。
• 定义编码器层。
• 编码器模型，将输入编码为潜在变量。
• 我们使用均值作为输出，因为它是中心点表示正太分布，。
• 我们从2个密集层的输出中进行采样。
• 在VAE模型中定义解码器层。
• 定义整体VAE模型，用于重建和训练。
• 定义生成器模型，根据潜变量z生成新数据。
• 将我们的损失翻译成Keras代码。
• 开始训练。

# 定义输入层
input_dim = X_train.shape[1]
inputs = Input(shape=(input_dim,))
# 定义 Encoder 层
n_z = 2
n_epoch = 200

h_q = Dense(512, activation='relu')(inputs)
mu = Dense(n_z, activation='linear')(h_q)
log_sigma = Dense(n_z, activation='linear')(h_q)

# Encoder model, to encode input into latent variable
# We use the mean as the output as it is the center point, the representative of the gaussian
encoder = Model(inputs, mu)

def sample_z(args):
    mu, log_sigma = args
    eps = K.random_normal(shape=(batch_size, n_z), mean=0., stddev=1.)
    return mu + K.exp(log_sigma / 2) * eps


# Sample z ~ Q(z|X)
z = Lambda(sample_z, name='sampleZ', output_shape=(n_z,))([mu, log_sigma])

# Define decoder layers in VAE model
decoder_hidden = Dense(512, activation='relu')
decoder_out = Dense(input_dim, activation='sigmoid')

h_p = decoder_hidden(z)
outputs = decoder_out(h_p)

# Overall VAE model, for reconstruction and training
vae = Model(inputs, outputs)

# Generator model, generate new data given latent variable z
d_in = Input(shape=(n_z,))
d_h = decoder_hidden(d_in)
d_out = decoder_out(d_h)
decoder = Model(d_in, d_out)

定义好模型以后，我们查看一下模型结构

print("encoder model structure：")
print(encoder.summary())
print()
print()
print("decoder model structure：")
print(decoder.summary())
print()
print()
print("vae model structure：")
print(vae.summary())

定义keras损失函数:

def vae_loss(y_true, y_pred):
    """ Calculate loss = reconstruction loss + KL loss for each data in minibatch """
    recon = K.sum(K.binary_crossentropy(y_pred, y_true), axis=1)
    kl = 0.5 * K.sum(K.exp(log_sigma) + K.square(mu) - 1. - log_sigma, axis=1)

    return recon + kl

 编译模型:

vae.compile(optimizer='adam', loss=vae_loss)
vae_history = vae.fit(X_train, X_train, batch_size=batch_size, shuffle=True, 
                      validation_data = (X_val, X_val),
                    epochs=n_epoch, callbacks = [EarlyStopping(monitor='loss',patience = 3)])

评估

plt.plot(vae_history.history['loss'])
plt.plot(vae_history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
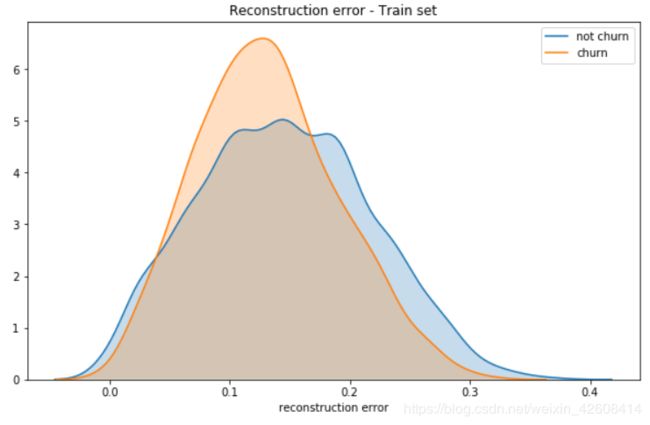
plt.show();

 在训练集中的误差分布

x_train_encoded = encoder.predict(X_train)

pred_train = decoder.predict(x_train_encoded)
mse = np.mean(np.power(X_train - pred_train, 2), axis=1)
error_df = pd.DataFrame({'recon_error': mse,
                        'churn': y_train})

plt.figure(figsize=(10,6))
sns.kdeplot(error_df.recon_error[error_df.churn==0], label='not churn', shade=True, clip=(0,10))
sns.kdeplot(error_df.recon_error[error_df.churn==1], label='churn', shade=True, clip=(0,10))
plt.xlabel('reconstruction error');
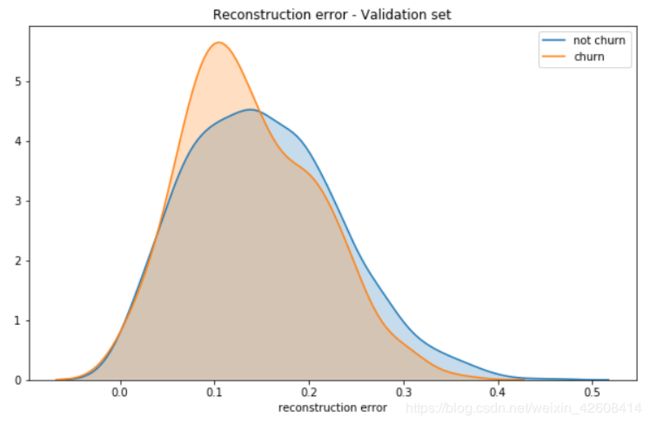
plt.title('Reconstruction error - Train set');

在验证集中的误差分布 

x_val_encoded = encoder.predict(X_val)
pred = decoder.predict(x_val_encoded)
mseV = np.mean(np.power(X_val - pred, 2), axis=1)
error_df = pd.DataFrame({'recon_error': mseV,
                        'churn': y_val})
plt.figure(figsize=(10,6))
sns.kdeplot(error_df.recon_error[error_df.churn==0], label='not churn', shade=True, clip=(0,10))
sns.kdeplot(error_df.recon_error[error_df.churn==1], label='churn', shade=True, clip=(0,10))
plt.xlabel('reconstruction error');
plt.title('Reconstruction error - Validation set');

潜变量空间可视化 

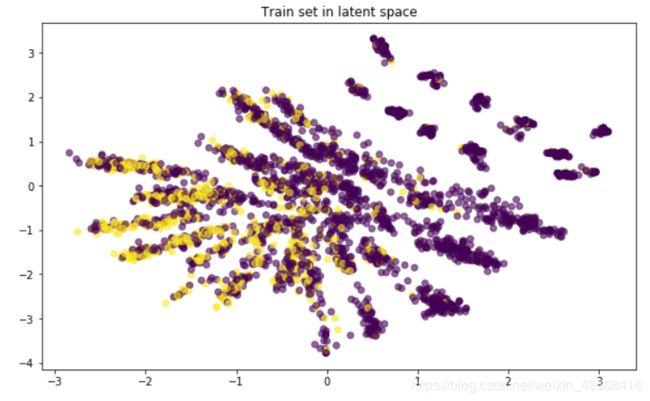
x_train_encoded = encoder.predict(X_train)

plt.scatter(x_train_encoded[:, 0], x_train_encoded[:, 1], 
            c=y_train, alpha=0.6)
plt.title('Train set in latent space')
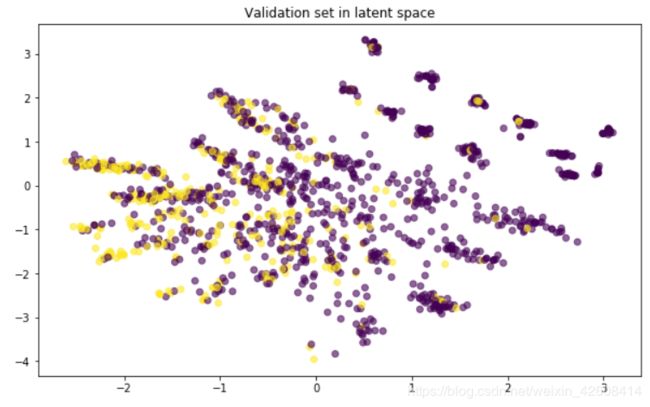
plt.show();

x_val_encoded = encoder.predict(X_val)

plt.scatter(x_val_encoded[:, 0], x_val_encoded[:, 1], 
            c=y_val, alpha=0.6)

plt.title('Validation set in latent space')
plt.show();

 

以上是在潜变量空间中对流失和未流失数据进行可视化，通过encoder模型将原始特征数据进行了降维，从原来特征的的45维(one-hot展开后)降至现在的2维，我们发现流失数据主要集中在图中的左下角区域,大致可分，但准确率应该不会很高。

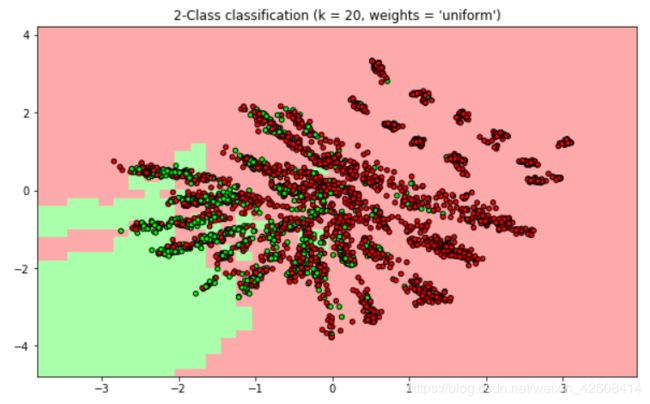
在潜变量空间中进行分类

下面我们使用KNN算法在潜变量空间中进行二分类

from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets
weights='uniform'
n_neighbors=20
clf = neighbors.KNeighborsClassifier(n_neighbors, weights=weights)
X=x_train_encoded
y=y_train
clf.fit(X, y)

h=0.2
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00'])
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),np.arange(y_min, y_max, h))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])

# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx, yy, Z, cmap=cmap_light)

# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold,
            edgecolor='k', s=20)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title("2-Class classification (k = %i, weights = '%s')"
            % (n_neighbors, weights));

 

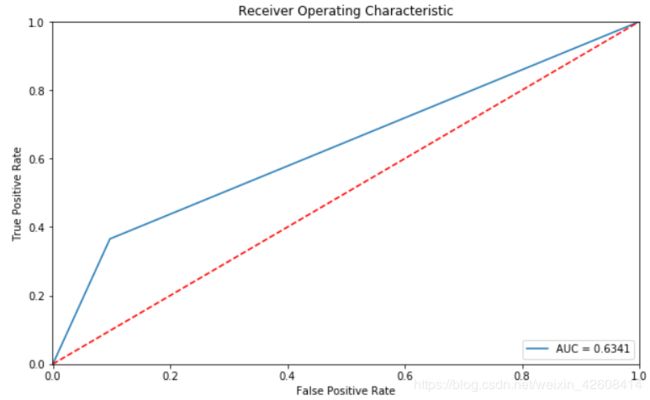
对分类模型进行评估 

x_val_encoded = encoder.predict(X_val)
fpr, tpr, thresholds = roc_curve(y_val, clf.predict(x_val_encoded))
roc_auc = auc(fpr, tpr)

plt.title('Receiver Operating Characteristic')
plt.plot(fpr, tpr, label='AUC = %0.4f'% roc_auc)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.xlim([-0.001, 1])
plt.ylim([0, 1.001])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show();

print('Accuracy:')
print(accuracy_score(y_val, clf.predict(x_val_encoded)))
print("Confusion Matrix:")
print(confusion_matrix(y_val,clf.predict(x_val_encoded)))
print("Classification Report:")
print(classification_report(y_val,clf.predict(x_val_encoded)))

 

 从上面的统计结果来看虽然准确率达到0.75，但是召回率很低，只有0.37.在实际的应用场景中我们更关心的是召回率。

VAE在MNIST 数据集中的实现

MNIST是一个用来训练识别手写数字(0-9)的图像数据集,数据集中包含了各种手写数字的图片如:

将VAE模型运用于MNIST数据集中，可以得到较好的识别效果，在潜变量空间中可以明显的看到 0-9分别位于各自不同的区域中,且识别的误差较小:

总结 

为什么用VAE来预测用户流失的误差要比预测MNIST大？个人觉得，与MNIST数据预测相比，用户流失是一个复杂的问题，可能还有更多用户流失的原因并未被搜集到当前数据中，要提高对流失用户的预测准确率，关键并不在预测模型，而是应该对用户流失原因的全面仔细分析同时引入更多更有价值的特征因子。

完整代码在此下载

https://github.com/tongzm/ml-python/blob/master/%E7%94%A8%E6%88%B7%E6%B5%81%E5%A4%B1%E9%A2%84%E6%B5%8B(VAE).ipynb