实战七：kaggle实战之房价预测

案例背景

       要求一个购房者描述心目中的好房子，他们可能不会从地下室的高度或者与铁路的远近开始说起。这个训练赛的数据集证明，价格谈判比卧室或栅栏数量更重要。数据集中共有79个解释性变量描述了住宅的每一个方面，比赛要求是对每个房子的最终价格进行预测。

第一步:导入基本的模块，并加载数据。

       首先引用numpy、pandas等必要模块，然后通过pandas的read_csv函数读入训练数据和测试数据。一般来说，数据集中的Id那一栏没有什么用，我们可以将其作为索引，之后检索起来也方便一些。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# index_col=0  将第0列作为行索引
train_df = pd.read_csv('D:\PyCharm\PycharmProjects\机器学习 七月！\kaggle_house_price/train.csv', index_col=0)
test_df = pd.read_csv('D:\PyCharm\PycharmProjects\机器学习 七月！\kaggle_house_price/test.csv', index_col=0)
print(train_df.head())
print(train_df.shape)

    

第二步：数据平滑及合并

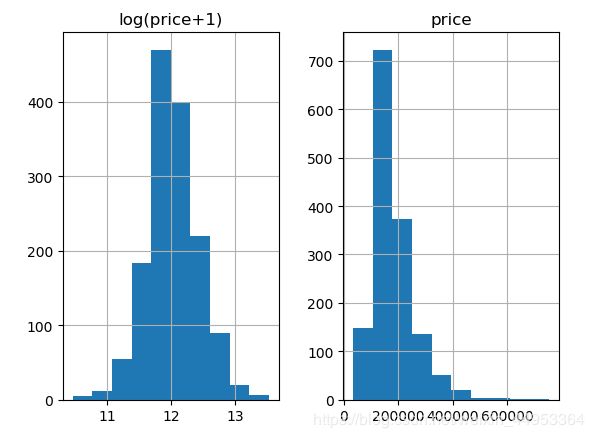
由于是对房屋价格进行预测，所以我们要注意价格的分布。通过下面的图片可以发现，房屋价格集中在200000附近的区间，这是一个比较偏的分布。为了使我们最后的更加精确，我们需要对价格进行平滑。这里我们使用log(price+1)来进行数据的平滑，可以看出，进行平滑之后的价格比较符合正态分布。log1p(x) 就是log(x+1)。  这里我们将数据进行了平滑，最后的预测结果就需要expm1()。 也就是将预测结果变为真实的房价数。   log1p反运算就是expm1()。

 kaggle平台提供了两张表，一张是带标签的数据（训练数据）， 一张是不带标签的数据（测试数据）。接下来，我想做的就是将带有标签数据的标签列删除，它也就变成不带标签的数据。在将测试数据与其进行合并。这么做主要是为了统一进行数据预处理的时候更加方便。等所有的需要的预处理进行完之后，我们再把他们分隔开。

prices = pd.DataFrame({'price': train_df['SalePrice'], 'log(price+1)': np.log1p(train_df['SalePrice'])})
prices.hist()  # 画图 看一下标签是否平滑
plt.show()

y_train = np.log1p(train_df.pop('SalePrice'))  # 将原来的标签删除 剩下log(price+1)列的数据
all_df = pd.concat((train_df, test_df), axis=0)  # 将train_df, test_df合并

第三步：特征工程（处理缺失值等）

数据集合并之后，我们就可以对整个数据集进行处理了。首先我们要注意变量的类型。比如，MSSubClass是一个类别型的变量而非数值型变量，尽管它是由数字来表示的。pandas会将这类数字符号当成数字处理。这样会使我们后面的模型训练不准确，所以我们要把它变回string类型。

# 有些数据的取值只有四五，或者可数个。这类数据我们转为one_hot编码

# 发现MSSubClass值应该是分类值
print(all_df['MSSubClass'].dtypes)  # int64
all_df['MSSubClass'] = all_df['MSSubClass'].astype(str)
print(all_df['MSSubClass'].value_counts())

把它变回string类型之后，我们的工作并没有完成。机器学习的模型处理类别型数据还是比较麻烦，我们还得将它变成数值型变量。这里，我们通过One-Hot（独热码）编码进行数据变换。在pandas中，可以使用get_dummies实现这一转换：

# 我们将category的变量转变为numerical表达形式
# 当我们用numerical来表达categorical的时候，要注意，数字本身有大小。
# 不能乱指定大小，我们采用one_hot编码
# pandas自带的get_dummies方法可以一键做到one_hot
print(pd.get_dummies(all_df['MSSubClass'], prefix='MSSubClass').head())
# 此刻MSSubClass被我们分成了12个column，每一个代表一个category。是就是1，不是就是0。

   

上面的结果显示，我们把MSSubClass这一列扩展成了很多列，每一列只有0和1这两个值，这样我们就实现了类别型数据到数值型数据的转变。根据数据描述，有很多列都是类别型数据，所以我们要对所有类别型数据进行变换：

# 同理,我们把所有的category数据都转化为One_hot
all_dummy_df = pd.get_dummies(all_df)

全部转换之后，所有类别型的数据都已经转换成数值型。下面我们进行缺失值的处理。

# 统计每列缺失值情况
print(all_dummy_df.isnull().sum().sort_values(ascending=False).head())

可以看到，缺失最多的列是LotFrotage，其次是GarageYrBlt。处理缺失信息需要我们好好审题。一般来说，数据集的描述中会写清楚这些缺失代表什么。当然，如果没有写明，也只能靠猜了…这里，我们用平均值填补缺失值。

# 我们用均值填充
mean_cols = all_dummy_df.mean()
all_dummy_df = all_dummy_df.fillna(mean_cols)

# 再检查一下是否有缺失值
print(all_dummy_df.isnull().sum().sum())    #0

接着，我们将数值型数据标准化。在进行回归预测时，我们应该尽量把数据集放在一个标准分布内，不能让数据之间的差距太大。当然，我们不需要把进行One-Hot编码的那些数据标准化，我们的目标是那些本来就是数值型的数据。下面先来看看哪些数据本来就是数值型的：

# 先找出数字型数据
numeric_cols = all_df.columns[all_df.dtypes != 'object']
print(numeric_cols)

标准化numerical数据，这一步并不是必要，但是得看你想要用的分类器是什么。一般来说，regression的分类器都比较傲娇，最好是把源数据给放在一个标准分布内。不要让数据间的差距太大。

用这种方式进行数据平滑：                                         

# 对其标准化
numeric_col_mean = all_dummy_df.loc[:, numeric_cols].mean()
numeric_col_std = all_dummy_df.loc[:, numeric_cols].std()
all_dummy_df.loc[:, numeric_cols] = (all_dummy_df.loc[:, numeric_cols]-numeric_col_mean) / numeric_col_std

把数据集分回训练集和测试集：

# 将合并的数据此时进行拆分  分为训练数据和测试数据
dummy_train_df = all_dummy_df.loc[train_df.index]
dummy_test_df = all_dummy_df.loc[test_df.index]

到此我们分别进行了：

1. 将训练数据和测试数据进行合并，主要是为了方便进行统一处理；
2. 将category型的数据转化为one_hot编码；
3. 对缺失值进行填充；
4. 标准化数据；
5. 将合并的数据又分开。

第四步：模型训练

 模型1：岭回归-Ridge Regression

首先把数据放到岭回归模型里面跑一遍看看（对于多因子的数据集，这种模型可以把所有变量都无脑地丢进去）。

from sklearn.linear_model import Ridge
from sklearn.model_selection import cross_val_score
 
X_train = dummy_train_df.values
X_test = dummy_test_df.values
 
#用sklearn自带的交叉验证方法来测试模型：
alphas = np.logspace(-3, 2, 50)
test_scores = []
for alpha in alphas:
    clf = Ridge(alpha)
    test_score = np.sqrt(-cross_val_score(clf, X_train, y_train, cv=10, scoring='neg_mean_squared_error'))
    test_scores.append(np.mean(test_score))
 
# 看那个alpha下 模型预测的更好
plt.plot(alphas, test_scores)
plt.title('Alpha vs CV Error')
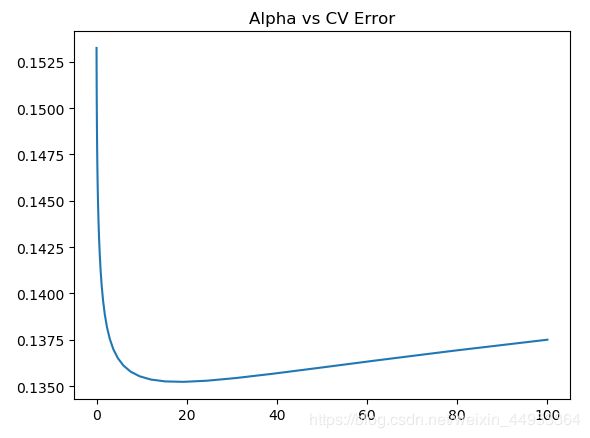
plt.show()

根据图象可以看出，alpha在15左右时，模型最佳。均方误差大概在0.136左右。

模型二：随机森林（基本模型我们设为岭回归。一般默认为回归树）

from sklearn.ensemble import RandomForestRegressor
 
max_features = [0.1, 0.3, 0.5, 0.7, 0.9, 0.99]
test_scores = []
for max_feat in max_features:
    clf = RandomForestRegressor(n_estimators=200, max_features=max_feat)
    test_score = np.sqrt(-cross_val_score(clf, X_train, y_train, cv=5, scoring='neg_mean_squared_error'))
    test_scores.append(np.mean(test_score))
plt.plot(max_features, test_scores)
plt.title('Max Features vs CV Error')
plt.show()

 max_features 代表的划分是考虑的最大特征数，可以是大于1的具体数字， 代表考虑多少个特征。 如果是小于1的数字，代表的是特征的百分之多少。

当max_feature为0.3时，随机森林的错误最小，大概在0.137左右。

模型三：Stacking集成 （用stacking的思维来汲取两种或多种模型的优点）

# 我们用一个Stacking的思维来汲取两种或多种模型的优点
ridge = Ridge(alpha=15)
rf = RandomForestRegressor(n_estimators=500, max_features=0.3)
 
ridge.fit(X_train, y_train)
rf.fit(X_train, y_train)
 
# 上面提到了，因为最前面我们给label做了个log(1+x), 于是这里我们需要把predit的值给exp回去，并且减掉那个"1"
# 所以就是我们的expm1()函数。
 
y_ridge = np.expm1(ridge.predict(X_test))
y_rf = np.expm1(rf.predict(X_test))
 
y_final = (y_ridge + y_rf) / 2
submission_df = pd.DataFrame(data={'ID': test_df.index, 'SalePrice': y_final})
print(submission_df)

   submission_df 就是我们这场比赛需要提交的结果。也就是测试样本的预测值。

模型四： bagging模型

from sklearn.ensemble import BaggingRegressor
from sklearn.model_selection import cross_val_score

params = [1, 10, 15, 20, 25, 30, 40]
test_scores = []
for param in params:
    clf = BaggingRegressor(n_estimators=param, base_estimator=Ridge(15))    # 基模型为岭回归
    test_score = np.sqrt(-cross_val_score(clf, X_train, y_train, cv=10, scoring='neg_mean_squared_error'))
    test_scores.append(np.mean(test_score))
plt.plot(params, test_scores)
plt.title('n_estimator vs CV Error')
plt.show()

bagging就是把多个小分类器放在一起，每个train随机选取一部分，然后把他们的最终结果综合起来（投票制）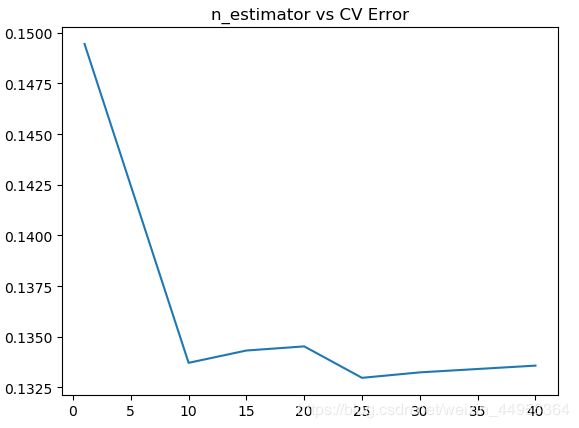

图片显示Bagging的效果还是不错的，在包含25个基分类器的时候错误率约为0.133。比前面的几种模型好

 模型五：Adaboost

from sklearn.ensemble import AdaBoostRegressor

params = [1,3,5,8,10,15]
test_scores = []
for param in params:
    clf = AdaBoostRegressor(n_estimators=param, base_estimator=Ridge(15))
    test_score = np.sqrt(-cross_val_score(clf, X_train, y_train, cv=10, scoring='neg_mean_squared_error'))
    test_scores.append(np.mean(test_score))

plt.plot(params, test_scores)
plt.title("n_estimator vs CV Error")
plt.show()

Adaboos+Ridge, 用3个弱分类器的情况下，均方误差能降到0.141左右。

模型六：Kaggle神器：XgBoost

from xgboost import XGBRegressor

# 用sklearn自带的cross validation方法来测试模型
params = [1,2,3,4,5,6]
test_scores = []
for param in params:
    clf = XGBRegressor(max_depth=param)
    test_score = np.sqrt(-cross_val_score(clf, X_train, y_train, cv=10, scoring='neg_mean_squared_error'))
    test_scores.append(np.mean(test_score))
plt.plot(params, test_scores)
plt.title("max_depth vs CV Error")
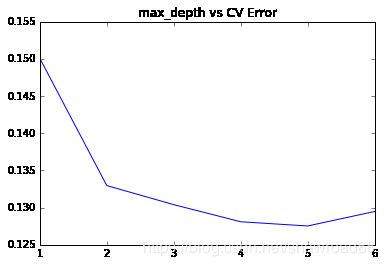
plt.show()

深度为5的时候，错误率缩小到0.127