斯坦福大学机器学习笔记——逻辑回归、高级优化以及多分类问题

shi先简单说一下逻辑回归，其实会有很多人误解，会将逻辑回归当成回归算法，其实逻辑回归就是我们所说的分类问题，所谓的逻辑，一般我们说的逻辑就是逻辑0或者逻辑1，所以可以借此理解。但是逻辑回归不仅仅只包括两分类问题，它还包括多分类问题。
那么能否使用线性回归的思想解决逻辑回归吗，我们从以下两方面考虑：
1. 假设如下图所示的数据集:

假设使用线性回归来拟合该数据集，当出现一个较大的波动点时（最右侧的点），则拟合得到的曲线为蓝色的线，当大于0.5时，判断为1，小于0.5时判断为0（等于0.5判断为哪一类无所谓，以后遇到同样的问题，采用相同的处理方式），会出现很多的误差点。
2.采用线性回归得到的拟合曲线，在进行判断时会出现很多大于1或者小于0的点，对于分类问题则明显是不合适。
我们下面说学的方法就是逻辑回归的算法，它的输出永远在0~1之间。

逻辑回归的假说（hypothesis）：
逻辑回归假说的表达式应该满足我们上面提到的特性，它的输出值永远在0~1之间，当大于0.5时，判断为0；当小于0.5时判断为1。
所以我们采用逻辑回归假说的形式为：

hθ(x)=g(θTx)=11+e−θTx

其中，g代表逻辑函数，也叫作sigmoid函数，它是一种常用的S形函数，公式为：

g(z)=11+e−z

它的图像为：

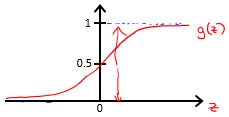
hθ(x) 的作用：对于给定的输入变量x，根据选择的参数 θ 计算输出变量为1的概率，即

hθ(x)=P(y=1|x;θ)=1−P(y=0|x;θ)

例如，在给定的x和 θ 的情况下，计算得到的 hθ(x) =0.7，则说明该样例有70%的可能性为正例。

决策边界（decision boundary）：
其实最终判断为0还是判断为1，我们一般采用的标准是：
当输出大于或等于0.5时，判断为1；小于0.5时，判断为0。
对于上面的逻辑函数：

hθ(x)=g(θTx)=11+e−θTx

当 θTx 大于等于0时，判断为1；当 θTx 小于0时，判断为0。
决策边界的含义实际就是找到能够正确划分我们数据集为两类（对于两类问题）的边界，下面举例来说明一下：

对于上面的数据集，我们可以判断当 θ=[−3,1,1] 时，可以实现数据的划分，则对应的直线为 θTx=−3+x1+x2 ，对于上述数据集的决策边界为 −3+x1+x2=0 ，当 −3+x1+x2≥0 时，判断为1，当 −3+x1+x2<0 时，判断为0，所以决策边界为 −3+x1+x2=0 。
需要注意的是：
决策边界是 hθ(x) ，决定于 θ ，它不是数据集的属性。它的确定过程为：
数据 → 确定参数 → 分类边界 → 预测结果

代价函数（cost function）：
对于线性回归，我们采用的代价函数为：误差平方和（均方误差）即， J(θ)=1m∑mi=112(hθ(x(i)−y(i)))2 ，如果对于逻辑回归， hθ(x)=11+e−θTx ，带入到平方误差和公式中会使得对于参数 θ，J(θ) 为非凸函数，所以对于逻辑回归来说，线性回归的代价函数不适用。
我们定义逻辑回归的代价函数为：

J(θ)=1m∑i=1mCost(hθ(x(i)−y(i)))

其中，

Cost(hθ(x)−y)={−log(hθ(x))−log(1−hθ(x))if y=1if y=0

该函数的形式是从极大似然中得到的。
该函数的曲线为：

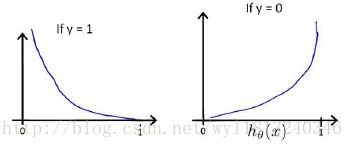
该函数对于 θ 是凸函数。
可以将上面的分段函数进行合并，合并后的式子为：

所以逻辑回归的损失函数为：

逻辑回归的梯度下降：
逻辑回归的梯度下降法与线性回归的梯度方法相同，可以查考线性回归的博客：
(http://blog.csdn.net/wyl1813240346/article/details/78395541)

仔细观察你会发现，逻辑回归算法的更新和线性回归的更新相同，但是他们只是形式上相同，通过上面我们可以观察到，他们的假设形式是不相同的，对于线性回归算法，假设为： hθ(x)=θTx ；而对于逻辑回归来说，假设的形式为： hθ(x)=11+e−θTx ，所以逻辑函数的梯度下降与线性回归的梯度下降实际上是两个完全不同的东西。
需要注意的是：
在我们学习线性回归的时候，使用梯度下降法需要使用特征缩放，以实现更快的收敛，在逻辑回归时，仍然需要使用特征收缩，实现更快的收敛。

高级优化
首先我们换个角度思考梯度下降法，对于梯度下降法我们想让它工作，我们需要计算两个量，一个是当前迭代次数的代价函数（实际编写代码时不需要计算，但是为了更好的观测算法是否收敛，所以计算该变量的值）和J等于0,1,…,n时的偏导数项。
然而还有一些更高级更复杂的优化算法实现代价函数的最小化，它们包括共轭梯度法、BFGS和L-BFGS等。
这三种方法的优缺点：

1. 不需要手动的调节学习率，在梯度下降法中我们可以知道，当学习率设置不恰当时会导致收敛速度很慢或者不能收敛，而上述三种方法，不需要手动设置，可以自动的寻找最适合的学习率。
2. 收敛速度相对于梯度下降法快了很多。
3. 但是以上三种方法的复杂度相对于梯度下降法复杂很多，对于现在来说，我们只需要会用。

下面举例来说明如何使用一些高级优化算法：

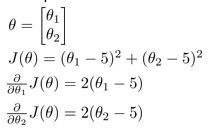
对于上述问题我们编写一个函数，来计算代价函数以及代价函数对于每个参数的偏导数，函数的代码如下所示：

function [jVal, gradient] = costFunction(theta)
jVal = (theta(1)-5)^2 + (theta(2)-5)^2;
gradient = zeros(2,1);
gradient(1) = 2*(theta(1)-5);
gradient(2) = 2*(theta(2)-5);
end

该函数输入为参数 θ ，输出为代价函数的值，以及代价函数对于每个参数的偏导数。运行完这个costFunction函数之后，就可以调用高级的优化函数fminunc，它是一种无约束最小化的函数，它的使用方式为：

options = optimset(‘GradObj’, ‘on’, ‘MaxIter’, ‘100’);
initialTheta = zeros(2,1);
[optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);

其中，options中存放了该优化函数需要的一些参数，对于上述代码来说，设置的梯度目标参数为打开，这意味着必须为该算法提供一个梯度，第二项给定了迭代得最大代数为100。@符号代表了我们刚刚定义函数的指针，同时需要注意的是对于fminunc函数来说，第二个参数的维度至少是二维的。调用该函数之后，你就使用了众多高级算法中的一个。

多分类问题：
在上述表述中，我们大都基于二分类进行表述的，但是在我们生活中经常遇见多分类问题，比如，我们对我们的邮件分类，分为家人邮件（类标为1）、工作邮件（类标为2）、朋友邮件（类标为3）等多种类别，那我们如何处理多分类问题呢，这是我们下面要学习的。
对于二分类的数据集，可以用下面的图形进行表示：

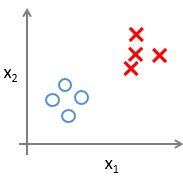
而对于多分类（以三类为例），可以用下面的图形表示：

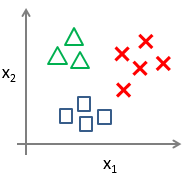
对于三分类问题，我们可以使用二分类问题的解决方案来解决，下面我们将介绍怎样进行一对多的分类工作，该方法也称为“一对余”。该方法的具体实现过程如下：
对于上述训练样本，我们需要建立一个伪数据集，比如将上面的三角形最为正类（类标为1），正方形和×作为负类（类别为0），得到的数据集的图形表示如下：

使用该训练样本训练模型，得到一个假设 h(1)θ(x) ，该假设代表判断为三角形类别的概率；
同理，我们将正方形作为正类（类标为2），三角形和×作为负类（类标为0），得到的数据集的图形表示吐下：

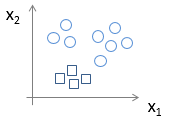
使用该训练样本训练模型，得到一个假设 h(2)θ(x) ，该假设代表判断为正方形类别的概率；
同理我们将×作为正类（类标为3），三角形和正方形作为负类（类标为0），得到的数据集的图形表示吐下：

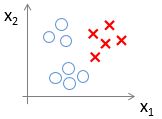
使用该训练样本训练模型，得到一个假设 h(3)θ(x) ，该假设代表判断为×类别的概率；
若是多分类，则一直将此过程进行下去。最终得到 n 个假设（其中n代表类别个数）。
当训练结束之后，对于待测试样本 x∗ ，分别计算在各个假设中的值 h(1)θ(x∗)、h(2)θ(x∗)、h(3)θ(x∗) ，上述假设分别对应于判断为类别1（三角形）、类别2（正方形）和类别3（×）的概率，比较每个概率的大小，选取最大的假设值对应的类别作为测试样本的类别。
上述就是“一对余”多分类问题的全部过程。

本人也是菜鸟一枚，写此博客也是互相学习的过程，有不对的地方欢迎指正，谢谢！