A*算法

1.什么是A*算法？

A*算法是静态路网中求解最短路径最有效的直接的搜索方法，但是它非常耗时，遍历周围所有节点，查找出最优路径，下面为我再Mono中写的四个脚本供大家参考。

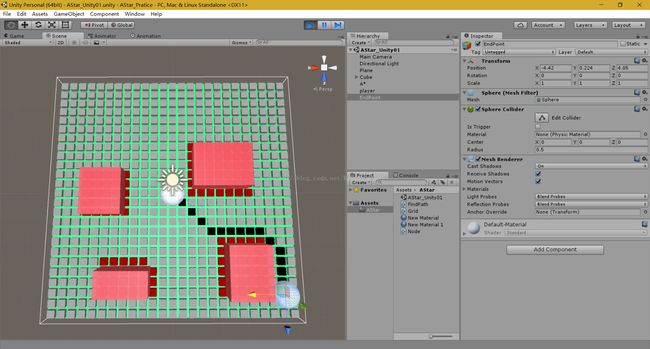
1.首先搭建戏台子。第一步打开unity，创建一个Plane，四个Cube，两个Sphere，一个改名为Player，一个为EndPoint,其中一个Cube作为父物体，，把另外三个Cube设为其子物体，并且给这个父物体Cube

设置层为UnWalkable层，给Cube和Plane分别上色，然后创建一个空物体名为A*,效果图如下图所示:

2.开始写脚本

A*算法是居于网格的导航，所以必须用到Unity中自带的Grid和Node组件

第1个脚本

挂载对象：不挂载

作用：供其他脚本调用

注意：不继承Mono

using UnityEngine;
using System.Collections;
public class Node
{
    public bool _canWalk;
    //该节点是否可以通过
    public Vector3 _worldPos;
    //该节点的位置
    public int _gridX, _gridY;
    //该网格的索引，取得节点
    public int gCost;
    //起始点与该节点的长度
    public int hCost;
    //目标点与该节点的长度
    public int fCost {//f的值是G和H的和,该节点和该路径的评分
        get { return gCost + hCost; }
    }
    public Node parent;
    //指向父对象的指针
    public Node (bool CanWalk, Vector3 Position, int x, int y)//构造函数
    {
        _canWalk = CanWalk;
        _worldPos = Position;
        _gridX = x;
        _gridY = y;
    }
}

第2个脚本

挂载对象：空物体A*上

作用：合适的节点加入列表，不合适的点剔除列表

注意：

using UnityEngine;
using System.Collections.Generic;
public class Grid : MonoBehaviour
{
    private Node[,] grid;
    //定义grid二维数组
    public Vector2 gridSize;
    //二维向量保存网格的大小
    public float nodeRadius;
    //设定每个节点的半径
    private float nodeDiameter;
    //节点的直径
    public LayerMask WhatLayer;
    //节点的标签
    public int gridCntX, gridCntY;
    //保存每个方向上格子的个数
    public Transform player;
    // 玩家的引用
    public List<Node> path = new List<Node> ();
    //保存路径
    // Use this for initialization
    void Start ()
    {
        nodeDiameter = nodeRadius * 2;//计算节点的直径
        gridCntX = Mathf.RoundToInt (gridSize.x / nodeDiameter);//横轴需要多少个格子
        gridCntY = Mathf.RoundToInt (gridSize.y / nodeDiameter);//纵轴需要多少个格子
        grid = new Node[gridCntX, gridCntY];
        CreatGrid ();//创建节点
    }
    private void CreatGrid ()//创建节点形成网格
    {
        //起始点
        Vector3 startPoint = transform.position - gridSize.x / 2 * Vector3.right - Vector3.forward * gridSize.y / 2;
        for (int i = 0; i < gridCntX; i++) {
            for (int j = 0; j < gridCntY; j++) {
                //节点的真实位置
                Vector3 worldPoint = startPoint + Vector3.right * (i * nodeDiameter + nodeRadius) +
                                     Vector3.forward * (j * nodeDiameter + nodeRadius);
                //节点是否可以行走
                bool walkable = !Physics.CheckSphere (worldPoint, nodeRadius, WhatLayer);//圆形的射线
                grid [i, j] = new Node (walkable, worldPoint, i, j);
            }
        }
    }
    //获取节点的位置
    public Node GetFromPosition (Vector3 postion)
    {
        //在横轴上的相对位置
        float percentX = (postion.x + gridSize.x / 2) / gridSize.x;
        //在纵轴的相对位置
        float percentY = (postion.z + gridSize.y / 2) / gridSize.y;
        percentX = Mathf.Clamp01 (percentX);
        percentY = Mathf.Clamp01 (percentY);
        int x = Mathf.RoundToInt ((gridCntX - 1) * percentX);
        int y = Mathf.RoundToInt ((gridCntY - 1) * percentY);
        return grid [x, y];
    }
    void OnDrawGizmos ()//画出网格和节点
    {
        //画出网格的边缘
        Gizmos.DrawWireCube (transform.position, new Vector3 (gridSize.x, 1, gridSize.y));
        if (grid == null)
            return;
        //画出网格里面的节点
        foreach (var node in grid) {
            Gizmos.color = node._canWalk ? Color.white : Color.red;
            //为了有边缘让他大小减小0.1f
            Gizmos.DrawCube (node._worldPos, Vector3.one * (nodeDiameter - .1f));
        }
        //画出玩家的节点
        Node playerNode = GetFromPosition (player.position);
        if (playerNode != null && playerNode._canWalk) {
            Gizmos.color = Color.cyan;
            Gizmos.DrawCube (playerNode._worldPos, Vector3.one * (nodeDiameter - .1f));
        }
        //画出路径的颜色
        if (path != null) {
            foreach (var node in path) {
                Gizmos.color = Color.black;
                Gizmos.DrawCube (node._worldPos, Vector3.one * (nodeDiameter - .1f));
            }
        }

    }
    //获取节点格子周围节点的方法
    public List<Node> GetNeibourhood (Node node)
    {
        List<Node> neibourhood = new List<Node> ();
        for (int i = -1; i <= 1; i++) {
            for (int j = -1; j <= 1; j++) {
                if (i == 0 && j == 0) {
                    continue;
                }
                int tempX = node._gridX + i;
                int tempY = node._gridY + j;
                //是否越界
                if (tempX < gridCntX && tempX > 0 && tempY > 0 && tempY < gridCntY) {
                    neibourhood.Add (grid [tempX, tempY]);
                }
            }
        }
        return neibourhood;
    }
}

第3个脚本

//  挂载对象：空物体
// 功能：实现A*寻路实现路径
// 注意：
using UnityEngine;
using System.Collections.Generic;
public class FindPath : MonoBehaviour
{
    public Transform player, Endpoint;
    private Grid _grid;
    //整个网格的引用
    void Start ()
    {
        _grid = GetComponent<Grid> ();
    }
    void Update ()
    {
        FindingPath (player.position, Endpoint.position);
    }
    void FindingPath (Vector3 StartPos, Vector3 EndPos)
    {
        //获取开始和结束的节点
        Node startNode = _grid.GetFromPosition (StartPos);
        Node EndNode = _grid.GetFromPosition (EndPos);
        //开始集合
        List<Node> openSet = new List<Node> ();
        //结束集合
        HashSet<Node> closeSet = new HashSet<Node> ();
        //起点放到开始节点当中
        openSet.Add (startNode);
        //循环查询
        while (openSet.Count > 0) {
            Node currentNode = openSet [0];
            //遍历开启列表的所有元素
            for (int i = 0; i < openSet.Count; i++) {
                if (openSet [i].fCost < currentNode.fCost ||
                    openSet [i].fCost == currentNode.fCost
                    && openSet [i].hCost < currentNode.hCost) {
                    currentNode = openSet [i];
                }
            }
            openSet.Remove (currentNode);
            closeSet.Add (currentNode);
            //当前节点是否是结束节点，如果是结束查询
            if (currentNode == EndNode) {
                //生成路径
                GeneratePath (startNode, EndNode);
                return;
            }
            //选择最优的节点
            foreach (var node in _grid.GetNeibourhood(currentNode)) {
                //不需要操作直接跳过
                if (!node._canWalk || closeSet.Contains (node))
                    continue;
                //新的消费，当前格子与开始格子的距离
                int newCost = currentNode.gCost + GetDistanceNodes (currentNode, node);
                //新的消费比当前的消费小的时候，不在开始列表
                if (newCost < node.gCost || !openSet.Contains (node)) {
                    node.gCost = newCost;
                    node.hCost = GetDistanceNodes (node, EndNode);
                    node.parent = currentNode;
                    //没有包含节点，放到开始节点之中
                    if (!openSet.Contains (node)) {
                        openSet.Add (node);
                    }
                }
            }
        }
    }
    //生成路径
    private void GeneratePath (Node startNode, Node endNode)
    {

        List<Node> path = new List<Node> ();
        Node temp = endNode;
        while (temp != startNode) {
            path.Add (temp);
            temp = temp.parent;
        }
        path.Reverse ();
        _grid.path = path;
    }
    //获取两个节点距离的方法
    int GetDistanceNodes (Node a, Node b)
    {
        int cntX = Mathf.Abs (a._gridX - b._gridX);
        int cntY = Mathf.Abs (a._gridY - b._gridY);
        if (cntX > cntY) {
            //X轴更大
            return 14 * cntY + 10 * (cntX - cntY);
        } else {
            //Y轴更大
            return 14 * cntX + 10 * (cntY - cntX);
        }
    }
}

以上即为实现A*算法的所有脚本，挂载后把所需引用对象引用进去即可实现，最后实现的效果图如下：

最后A*算法虽然是路径最优算法，但是对资源的占用比较大，优化方法为二叉堆，这里暂时不做介绍，本文为本人纯手打，代码均为本人亲力手敲，如有雷同，纯属巧合。