数据结构与算法之美 | 单链表、双链表的增删改查（C++）

本系列内容专为课程面向笔/面试的《数据结构与算法》总结性精讲开设，以图文并茂的方式讲解数据结构，让大家打牢基础，促进对课程内容的掌握，最后做到题解大神，大厂offer拿到手软！

0. 数据结构图文解析系列

数据结构系列文章
数据结构图文解析之：单链表、双链表的增删改查（C++）
数据结构图文解析之：一文掌握栈Stack（真题讲解）
数据结构图文解析之：队列详解与C++模板实现
数据结构图文解析之：树的简介及二叉排序树C++模板实现.
数据结构图文解析之：AVL树详解及C++模板实现
数据结构图文解析之：二叉堆详解及C++模板实现
数据结构图文解析之：哈夫曼树与哈夫曼编码详解及C++模板实现

1. 线性表简介

线性表是一种线性结构，它是由零个或多个数据元素构成的有限序列。线性表的特征是在一个序列中，除了头尾元素，每个元素都有且只有一个直接前驱，有且只有一个直接后继，而序列头元素没有直接前驱，序列尾元素没有直接后继。

数据结构中常见的线性结构有数组、单链表、双链表、循环链表等。线性表中的元素为某种相同的抽象数据类型。可以是C语言的内置类型或结构体，也可以是C++自定义类型。

2. 单链表

单向链表是链表的一种。链表由节点所构成，节点内含一个指向下一个节点的指针，节点依次链接成为链表。因此，链表这种数据结构通常在物理内存上是不连续的。链表的通常含有一个头节点，头节点不存放实际的值，它含有一个指针，指向存放元素的第一个节点。

2.1 单向链表的节点结构

//节点结构
template <typename T>
class Node
{
public :
    T _value;
    Node* _next;
public:
    Node() = default;
    Node(T value, Node * next)
        : _value(value), _next(next){}
};

其中，

• _value: 节点的值
• _next： 指针，指向下一个节点

2.2 单向链表的抽象数据结构

//单链表
//phead: 链表的头节点。
//count: 链表元素个数。

template <typename T>
class SingleLink
{
public:
    typedef Node<T>*  pointer;
    SingleLink();
    ~SingleLink();
 
    int size();                         //获取长度
    bool isEmpty();                     //判空
 
    Node<T>* insert(int index, T t); //在指定位置进行插入
    Node<T>* insert_head(T t);         //在链表头进行插入
    Node<T>* insert_last(T t);         //在链表尾进行插入
 
    Node<T>*  del(int index);         //在指定位置进行删除
    Node<T>*  delete_head();         //删除链表头
    Node<T>*  delete_last();         //删除链表尾
 
    T get(int index);                 //获取指定位置的元素
    T get_head();                     //获取链表头元素
    T get_last();                     //获取链表尾元素
 
    Node<T>* getHead();                 //获取链表头节点
 
private :
    int count;
    Node<T> * phead;                
 
private :
    Node<T> * getNode(int index);      //获取指定位置的节点
};

2.3 单链表添加节点

链表的插入元素操作时间复杂度O（1），只需要进行指针的指向修改操作。

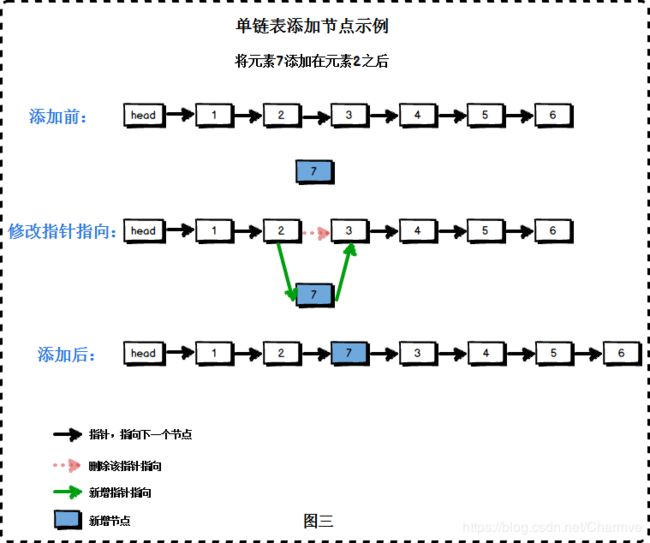
在2之后添加7：

1. 为元素7构建节点 。
2. 将节点2 的next指针指向节点7。
3. 将节点7的next指向节点3。（节点3 的位置要先保留起来）

/*
在指定位置插入新节点
*/
template <typename T>
Node<T>* SingleLink<T>::insert(int index, T t)
{
    Node<T> * preNode = getNode(index);
    if (preNode)
    {
        Node<T> *newNode = new Node<T>(t,preNode->_next);
        preNode->_next = newNode;
        count++;
        return newNode;
    }
    return nullptr;
};
/*
从头部插入
*/
template <typename T>
Node<T>* SingleLink<T>::insert_head(T t)
{
    return insert(0, t);
};
/*
从尾部进行插入
*/
template <typename T>
Node<T>* SingleLink<T>::insert_last(T t)
{
    return insert(count, t);
};

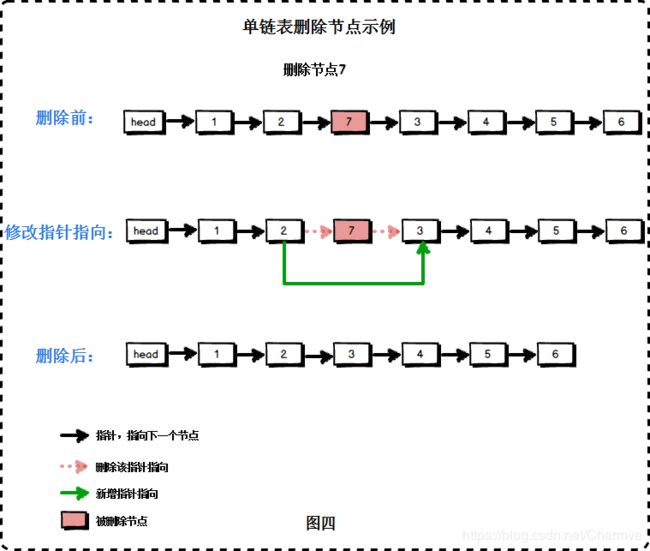
2.4 单链表删除节点

单链表的删除操作同样是一个时间复杂度O（1）的操作，它也只需要修改节点的指针指针后即可销毁被删除节点。

例如我们删除链表元素7：

相应的代码：

/*
删除链表指定位置元素
*/
template <typename T>
Node<T>* SingleLink<T>::del(int index)
{
    if (isEmpty())
        return nullptr;
    Node<T>* ptrNode = getNode(index);
    Node<T>* delNode = ptrNode->_next;
    ptrNode->_next = delNode->_next;
    count--;
    delete delNode;
    return ptrNode->_next;
};
/*
删除头节点
*/
template<typename T>
Node<T>* SingleLink<T>::delete_head()
{
    return del(0);
};
/*
删除尾节点
*/
template<typename T>
Node<T>*SingleLink<T>::delete_last()
{
    return del(count);
};

2.5 单链表代码测试

int main()
{
    SingleLink<int> link;
    for (int i = 0; i < 10; i++)
    {
        link.insert(i, i);
    }
    cout << link.size() << endl;
 
    link.insert_head(1111);
    link.insert_last(2222);
 
    SingleLink<int>::pointer ptr = link.getHead();
    while (ptr != nullptr)
    {
        cout << ptr->_value << endl;
        ptr = ptr->_next;
    }
 
    getchar();
    return 0;
}

测试结果：

10
1111
0
1
2
3
4
5
6
7
8
9
2222

其他的操作较为简单，不在这里贴出代码，课程中有完整的程序。

3. 双向链表

单链表的节点链接是单方向的，要得到指定节点的前一个节点，必须从头遍历链表。
双向链表是链表的一种。与单链表一样，双向节点由节点链接而成，每个节点含有两个指针，分别指向直接前驱与直接后继。从双向链表的任何一个节点开始都能够遍历整个链表。

我们将双向链表实现为双向循环链表，也即是最后一个元素的后继将指向头节点，整个链表形成一个循环。

例如，我们为元素1，2，3，4，5 构建一个双向循环链表

在图中：

• 表头为空。
• 表头的前驱节点是节点5，表头的后继节点是节点1；
• 节点1的前驱节点是表头，节点1的后继节点是节点2；
• 节点2的前驱节点是节点1，节点2的后继节点是节点3；
  …

3.1 双向链表节点结构

双向循环的节点中，比单向链表中多了一个指向直接前驱的指针

/*
双向链表的节点结构
*/
template <typename T>
struct Node
{
public:
    Node()= default;
    Node(T value, Node<T>* preptr, Node<T>* nextptr)
        :_value(value), pre_ptr(preptr), next_ptr(nextptr){}
 
public:
    T _value;
    Node<T>* pre_ptr;
    Node<T>* next_ptr;
};

说明：

• _value: 节点元素的值
• pre_ptr:指向直接前驱的指针
• next_ptr:指向直接后继的指针

3.2 双向链表的抽象数据结构

双向链表类的定义与单链表相似。

/*
* 双向链表类
*/
template<typename T>
class DoubleLink
{
public:
    typedef Node<T>* pointer;
public:
    DoubleLink();
    ~DoubleLink(){};
public:
    Node<T>* insert(int index, T value);
    Node<T>* insert_front(T value);
    Node<T>* insert_last(T value);
 
    Node<T>* del(int index);
    Node<T>* delete_front();
    Node<T>* delete_last();
 
    bool isEmpty();
    int size();
 
    T get(int index);
    T get_front();
    T get_last();
    Node<T>* getHead();
 
private:
    Node<T>* phead;
    int count;
private :
    Node<T>* getNode(int index);
};

3.3 双向链表添加节点

与单链表一样，双向链表添加节点的时间复杂度为O（1），它也只需要修改相关指针的指向。

/*
*将新节点插到第一个位置
*/
template <typename T>
Node<T>* DoubleLink<T>::insert_front(T value)
{
    Node<T>* newNode = new Node<int>(value, phead, phead->next_ptr);
    phead->next_ptr ->pre_ptr= newNode;
    phead->next_ptr = newNode;
    count++;
    return newNode;
};
/*
*将新节点插到链表尾部
*/
template <typename T>
Node<T>* DoubleLink<T>::insert_last(T value)
{
    Node<T> * newNode = new Node<int>(value, phead->pre_ptr, phead);
    phead->pre_ptr->next_ptr = newNode;
    phead->pre_ptr = newNode;
    count++;
    return newNode;
};
/*
*将节点位置插到index位置之前
*/
 
template <typename T>
Node<T>* DoubleLink<T>::insert(int index, T value)
{
    if (index == 0)
        return insert_front(value);
 
    Node<T>* pNode = getNode(index);
    if (pNode == nullptr)
        return nullptr;
    Node<T>* newNode = new Node<T>(value, pNode->pre_ptr, pNode);
    pNode->pre_ptr->next_ptr = newNode;
    pNode->pre_ptr = newNode;
    count++;
 
    return newNode;
};

3.4 双向链表删除节点

双向链表的删除操作时间复杂度为O（1）.我们删除节点7：

/*
*删除链表第一个节点
*返回删除后链表第一个节点
*/
template<typename T>
Node<T>* DoubleLink<T>::delete_front()
{
    if (count == 0)
    {
        return nullptr;
    }
    Node<T>* pnode = phead->next_ptr;
    phead->next_ptr = pnode->next_ptr;
    pnode->next_ptr->pre_ptr = phead;
    delete pnode;
    count--;
    return phead->next_ptr;
};
/*
*删除链表的末尾节点
*返回删除后链表尾部元素
*/
template<typename T>
Node<T>* DoubleLink<T>::delete_last()
{
    if (count == 0)
    {
        return nullptr;
    }
    Node<T>*pnode = phead->pre_ptr;
    pnode->pre_ptr->next_ptr = phead;
    phead->pre_ptr = pnode->pre_ptr;
    delete pnode;
    count--;
    return phead->pre_ptr;
}
/*
*删除指定位置的元素
*
*/
template <typename T>
Node<T>* DoubleLink<T>::del(int index)
{
    if (index == 0)
        return delete_front();
    if (index == count - 1)
        return delete_last();
    if (index >= count)
        return nullptr;
    Node<T>* pnode = getNode(index);
    pnode->pre_ptr->next_ptr = pnode->next_ptr;
    pnode->next_ptr->pre_ptr = pnode->pre_ptr;
 
    Node<T>* ptemp = pnode->pre_ptr;
    delete pnode;
    count--;
    return ptemp;
};

其他的接口实现都很简单，这里不再讲解。

3.5 双向链表代码测试

int main()
{
    DoubleLink<int> dlink;
    //插入测试
    for (int i = 0; i < 10; i++)
    {
        dlink.insert(0, i+10);
    }
    dlink.insert(0,  100);
    dlink.insert_last(1000);
    cout <<"链表长度:"<< dlink.size() << endl;
 
    //删除测试
    dlink.delete_front();
    dlink.delete_last();
    dlink.del(3);
 
 
    DoubleLink<int>::pointer ptr = dlink.getHead();
    ptr = ptr->next_ptr;
    while (ptr != dlink.getHead())
    {
        cout << ptr->_value<<endl;
        ptr = ptr->next_ptr;
    }
 
    getchar();
    return 0;
}

测试结果：

链表长度:12
19
18
17
15
14
13
12
11
10

- END-

最后奉上数据结构与算法之美专栏中的精彩文章

推荐阅读：

[1] 数据结构与算法 | 二分查找：剑指offer53 在排序数组中查找数字

[2] 数据结构与算法 | 数据结构中到底有多少种“树”？一文告诉你

[3] 数据结构与算法之美 | 二分查找：剑指offer53 在排序数组中查找数字

[4] Charmve Coding | Codility - Counting Elevator Movements

[5] Charmve Coding | the smallest positive integer that does not occur in Array A

[6] 华为研发编程测试题（四）试题及答案参考

关注微信公众号：迈微电子研发社，获取更多精彩内容，首发于个人公众号。

△微信扫一扫关注「迈微电子研发社」公众号

知识星球 (付费群) ：社群旨在分享秋招/春招准备攻略（含刷题）、面经和内推机会、学习路线、知识题库等。

△扫码加入「迈微电子研发社」学习辅导群