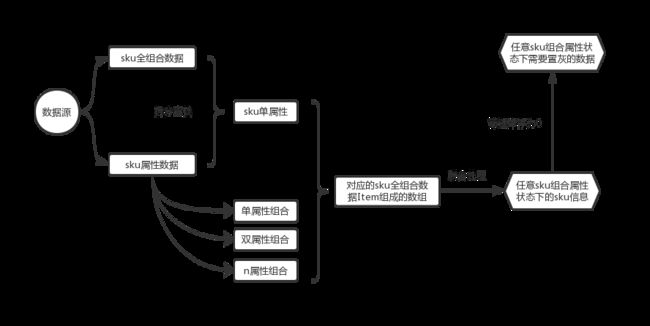
两万字长文-电商sku组合查询状态细究与实现

最近做到一个需求，需要做一个类似于京东或者淘宝等电商的商品详情页，其中有一个功能就是商品SKU的选择查询问题

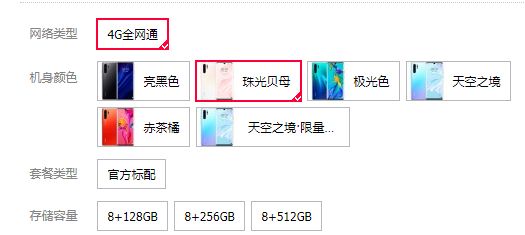
如上图，网络类型、机身颜色、套餐类型、存储容量这些每一个都是一个 SKU属性，当选择好了所有的 SKU属性后，会组合成一个完整的 SKU，对应一个具体的商品，然后就可以给出这条 SKU对应的商品的库存和价格等信息

并且，当点选了某些 SKU属性后，会自动根据当前已经点选的 SKU属性，来计算出当前条件下库存为 0 的 SKU组合，给予按钮置灰不可选的交互

一开始接到这个需求的时候，评审需求的后端和同组合作的前端小伙伴都认为这是一个难点，需要好好调研考量一下，而我则是邪魅一笑，觉得这东西不就是一个组合嘛，算法能写就写，不能写大不了来个暴力循环查找，小场面啦

然而，当我开始着手做的时候才发现跟平常确实不一样，这些代码好像不能闭着眼睛写

实现思路

当我发现这个功能确实有点小难度的时候，我就开始在网上搜相关文章了，这才发现相关文章好像都写的比较煞有其事，跟什么《你绝对不知道的数组的十种用法》什么《原型链全场最佳分析》什么《我的函数式编程不可能那么可爱》什么《三年前端大厂面试经历》都不太一样，看起来居然需要带着脑子，而且相关文章较少，除去那些抄来抄去的以及我没搜到的之外，几篇真正有实用价值的：

• 电商平台商品 SKU 组合查询算法实现
• sku 多维属性状态判断算法
• 淘宝SKU组合查询算法实现

我看完之后，顿时陷入了沉思

既然塑料恐龙是塑料做的，而塑料来源于石油，石油又是远古恐龙尸体转化成的。
那么是不是说，塑料恐龙就是真的恐龙？

这些文章描述得感觉不是很清楚，主要是没有完整可运行代码，看的云里雾里的，照着他们说的来做，还不如我自己重新写个，不过还是有些借鉴意义的

• 首先，给定几组 SKU的属性，那么根据这些属性组合出来的 sku肯定是可以被全部列举出来的，而且考虑到现实业务使用中，属性并不会太多，无需关心极端情况，所以哪怕全部穷举，对性能也没多大损耗；
• 然后，既然穷举出了所有的可能集合，那么就能计算出每一个组合对应的价格和存库等信息，这样一来自然就可以形成一个字典了，无论选择了哪些组合，都能从这个字典上快速查询到对应的价格和库存等信息，即以空间换时间，只要在开始时初始化好了这个包含所有可能的数据字典，后续 sku属性的切换无非是字典 key的变化

当然了，思路是这个思路，但是真正写代码的时候，需要考虑的点比较多，而且都要考虑到，无论少了哪一点，数据就会都不对了

数据准备

假设对于手机这个品类来说，它的 sku属性有成色、颜色、配置、版本，其中成色分为 全新、仅拆封，颜色分为深空灰、银色、金色，配置分为64G、256G，版本分为国行、港澳版、日韩、其他版本

每个 sku属性肯定都有自己独一无二的标识 ID，例如，对于颜色来说，它肯定有自己的 ID，称为 paramId，颜色下存在至少一个小属性，例如深空灰、银色、金色，每种颜色也都有自己的 ID，称为 valueId，结构如下：

interface ISkuParamItem {
  paramId: string
  paramValue: string
  valueList: Array<{
    valueId: string
    valueValue: string
  }>
}

请求 sku数据的时候，后端会将当前商品ID(称为 spuId)对应的所有sku属性返回，称为 sku属性数据集合数据格式暂定如下：

[{
    "paramId": "6977",
    "paramValue": "成色",
    "valueList": [{
        "valueId": "1081969",
        "valueValue": "全新"
    }, {
        "valueId": "1080699",
        "valueValue": "仅拆封"
    }]
}, {
    "paramId": "6975",
    "paramValue": "颜色",
    "valueList": [{
        "valueId": "730003",
        "valueValue": "深空灰色"
    }, {
        "valueId": "730004",
        "valueValue": "银色"
    }, {
        "valueId": "730005",
        "valueValue": "金色"
    }]
}, {
    "paramId": "7335",
    "paramValue": "配置",
    "valueList": [{
        "valueId": "710004",
        "valueValue": "64G"
    }, {
        "valueId": "710006",
        "valueValue": "256G"
    }]
}, {
    "paramId": "72",
    "paramValue": "版本",
    "valueList": [{
        "valueId": "1080627",
        "valueValue": "国行"
    }, {
        "valueId": "1080628",
        "valueValue": "港澳版"
    }, {
        "valueId": "1080697",
        "valueValue": "日韩"
    }, {
        "valueId": "1080629",
        "valueValue": "其他版本"
    }]
}]

当前商品ID(称为 spuId)对应的所有 sku数据返回，称为 商品全sku数据集合 数据格式暂定如下：

[
  {
      count: 98,
      paramIdJoin: "72_1080697__6975_730004__6977_1081969__7335_710006",
      priceRange: [7000, 8978],
      spuDId: "98002993445"
  }
]

其中，paramIdJoin是 sku属性组合连接而成，可分为 72_1080697、6975_730004、 6977_1081969、 7335_710006这个四个单元，每个单元又由 paramId 和 valueId 连接而成，所以 72_1080697__6975_730004__6977_1081969__7335_710006的意思就是 版本为日韩、颜色为银色、成色为全新、配置为256G的 sku组合，对应的总库存 count为 98，价格范围为 7000 ~ 8978，即最低价是 7000，最高价是 8978（如果只有一个价格没有高、低价格之分，那数组中的项就是那一个价格就行了），spu的标识 id spuDId为 98002993445

需要注意的是，paramIdJoin 的值，例如72_1080697__6975_730004__6977_1081969__7335_710006，必须是按照 paramId进行升序（或者降序也可以，这里按照升序处理）进行连接的，72 < 6975 < 6977 < 7335，所以才有 72_1080697__6975_730004__6977_1081969__7335_710006这个拼接方式

这对于后续算法的优化有着显著的作用，不按照顺序也可以，但在数据量比较大的情况下，计算时间会比较长，很可能出现页面卡顿的情况

后端可能返回的数据结构和上面不一样，不过关系不大，无论后端返回的数据结构是什么样的，返回的信息肯定需要包括上面那些，因为这些都是必要数据，如果不一样，你只需要先行处理一下，处理成和上面一样的数据结构就行了，这是肯定可以做到的
有了上述数据，就可以开始写核心的处理代码了

分析思路

其实这里的功能就两个，那就是当选中或取消任意 sku属性的时候：

• 计算出此时 sku属性组合对应的价格和库存
  例如当前选中了颜色：银色、内存：64G、运营商：移动，这一组 sku属性对应的商品的价格和库存

• 计算出在此时的 sku属性组合之下，需要置灰哪些 sku组合
  例如当前选中了颜色：银色、内存：64G，这一组 sku属性的时候，剩下的哪些 sku属性与这两个已经选中的 sku组合后的组合库存为 0，则说明这些 sku属性应该要被置灰，也就是不让用户选中
  例如，银色 + 64G的库存为 0，则当选中银色的时候，就需要将 64G这个 sku属性置灰

对于第一点，比较简单，只需要拿到当前选中的 sku属性组合，然后在所有的 sku数据中去查找包含所选中的 sku属性的数据即可，就是一个遍历筛选操作，有难度的是第二点

无论当前选中了哪些 sku属性，都要从整个 sku数据中找到包含任意选中的 sku属性的数据，然后在这些数据中找出库存为 0的数据，再从这些数据中找到应该被置灰的 sku属性

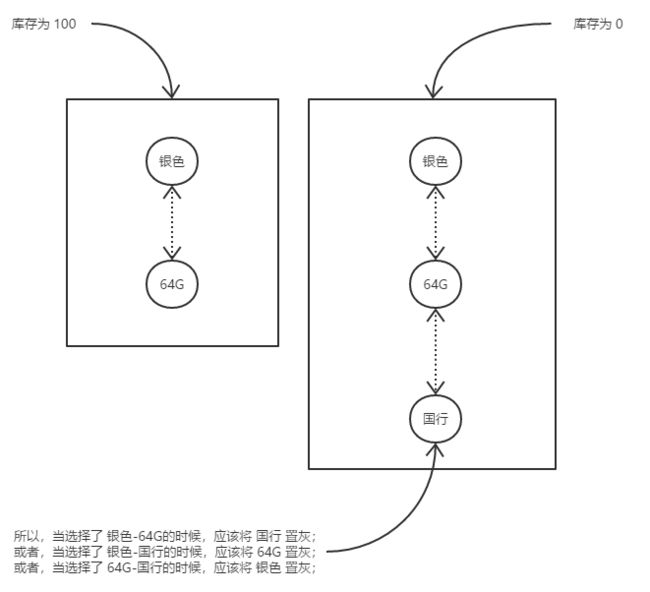
例如，假设 银色-64G-国行这个 sku的库存为 0，则当你选中 银色-64G的时候，应该把国行置灰，当选中 银色-国行，应该把64G置灰，当选中 国行-64G，应该把银色置灰

这只是最简单的一种情况

复杂一点，假设 银色-64G这个 sku的库存为 0，则当你选择银色的时候，，应该把64G置灰，当你选择64G的时候，，应该把银色置灰，当你选择深空灰-64G的时候，，应该把银色置灰……等等

如果 sku属性项有很多种，例如颜色、内存、运营商、制式、成色、套餐类型、保险，那么这种可组合的项就更多了

随便想一下，就感觉头好大，似乎是好多需要计算的东西啊

不过，其实也是有据可循的

当选中 n个 sku属性的时候，应该被置灰的 sku属性实际上就是 当选中这 n个中任一个sku属性时应该被置灰的 sku属性，加上当选中这 n个中任两个sku属性时应该被置灰的 sku属性，加上……加上当选中这 n个中任 n个sku属性时应该被置灰的 sku属性 头好像变得更大了

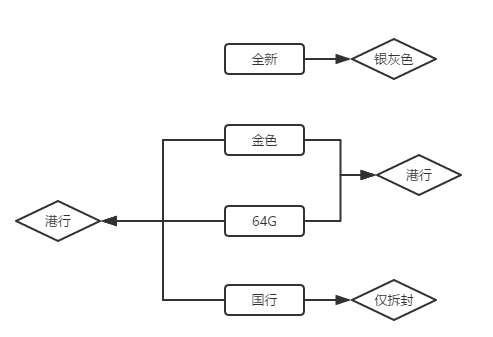
例如上图

当选中了 全新、金色、64G、国行这四个 sku属性的时候，计算在此状态下需要置灰的 sku属性：

首先，先看这四个 sku属性中，当不选中任何 sku属性时，有哪些 sku的库存为 0，发现所有的商品中，都没有 全新这个属性，则说明 全新的库存为 0，将之记录下来；

然后，再看这四个 sku属性中，每一个单独的 sku选中的时候应该置灰的 sku属性，例如当单独选中 全新这个 sku属性的时候，发现全新-银灰色这个组合的库存为 0，则将 银灰色置灰，将这个属性记录下来；当单独选中 国行这个 sku属性的时候，发现国行-仅拆封这个组合的库存为 0，则将 仅拆封置灰，将这个属性记录下来；当单独选中 金色或 64G的时候，其他任意一个sku属性与之组合皆有库存，则不记录任何 sku属性；

然后，再看这四个 sku属性中，当选中两个 sku的时候应该置灰的 sku属性，例如当同时选中 金色、64G这两个 sku属性的时候，发现金色-64G-港行这个组合的库存为 0，则将 港行置灰，将这个属性记录下来；当同时选中 全新-金色 或 全新-64G 或 全新-国行 或 金色-国行 或 64G-国行的时候，发现其他任一 sku与这些进行组合都有库存，则不记录任何 sku属性；

然后，再看这四个 sku属性中，当选中三个 sku的时候应该置灰的 sku属性，例如当同时选中 金色、64G这两个 sku属性的时候，发现金色-64G-港行这个组合的库存为 0，则将 港行置灰，将这个属性记录下来；当同时选中 全新-金色 或 全新-64G 或 全新-国行 或 金色-国行 或 64G-国行的时候，发现其他任一 sku与这些进行组合都有库存，则不记录任何 sku属性；

应该被置灰的意思就是对于当前 sku组合来说，如果再继续增加一个 sku属性，这个新的 sku组合对应的库存为 0，则说明最后增加的那个 sku属性应该被置灰

所以这里需要一个集合，这个集合包含当选择任意个数量 sku属性的时候，应该被置灰的 sku属性集合

想要得到这个集合，运算量会很大，而且绝大部分都是无用计算（计算出了一堆的结果，实际上用户只需要其中几个），所以简化一下，只需要得到一个集合，这个集合中包含了所有可能选择的 sku组合，还可以更加有序一点，将集合换成 Map，在 js中也就是对象，这个对象存在一些属性，这些属性的key值是数字 1、2、3……n-1, n，代表着选中 1 到 n个任意 sku属性，其值又是一个对象，这个小对象的 key就是 1 到 n个任意 sku属性的可能组合，其值包含这些组合的价格范围和库存等信息

代码层面的数据结构如下（部分）：

上述表示，对于选中了 1(下标为 0)个 sku属性的情况，共有 11种 sku选法，每种选法都有对应的 价格范围和总库存信息，例如 72_1080627表示，当选中了 版本为国行 这个 sku属性时，其价格范围数组 priceArr 和总库存 totalCount；对于选中了 2(下标为 1)个 sku属性的情况，共有 44种 sku选法，每种选法都有对应的 价格范围和总库存信息，例如 72_1080627__6975_730003表示，当选中了 版本为国行，颜色为深空灰色 这个 sku属性时，其价格范围数组 priceArr 和总库存 totalCount……等等

有了这个信息，后面就好办了

首先，你选中任意个 sku属性，我都能从这个集合里找出对应的总库存和价格范围，无需在原数据中多次筛选，这实现了第一个功能点；
对于第二个功能，当选中任意个 sku属性时(设为 n)，我只需要在这个对象中选取 key为从 0到 n的数据，并且找这些数据对应的 sku的总库存为 0的数据，这些数据中包含 sku属性就都是需要置灰的，这就实现了第二个功能点

所以，最关键的就是这个Map对象了，只要计算出这个Map对象，其他的就好办了，当然，说起来简单，真正用代码实现还是有很多需要注意的地方的

数据计算

计算单 sku属性所属下标集合

即从接口返回的包含了所有 sku属性组合及其对应的数据的数据源中（也就是前面所说的 商品全sku数据集合），计算出包含了每一个 sku属性的数据项的下标的集合

比如，对于 颜色：黑色 这个 sku属性，商品全sku数据集合数据中所有包含 颜色：黑色这个 sku属性的数据的下标的集合，就是其所属下标集合，以 sku属性的 paramId和 valueId为 key，以下标集合为值，则可以得到一个集合，数据结构如下：

{
    "6977_1081969": [0, 4, 5, 6, 7, 11, 14, 15, 17, 19, 20, 23, 25, 31, 32, 34, 35, 36, 38, 39, 40, 42, 44, 47],
    "6977_1080699": [1, 2, 3, 8, 9, 10, 12, 13, 16, 18, 21, 22, 24, 26, 27, 28, 29, 30, 33, 37, 41, 43, 45, 46],
    "6975_730003": [4, 14, 17, 18, 22, 23, 28, 29, 32, 33, 37, 39, 43, 44, 45, 47],
    "6975_730004": [0, 2, 5, 7, 8, 10, 12, 16, 19, 20, 24, 31, 34, 40, 41, 46],
    "6975_730005": [1, 3, 6, 9, 11, 13, 15, 21, 25, 26, 27, 30, 35, 36, 38, 42],
    "7335_710004": [1, 3, 4, 5, 8, 9, 10, 11, 19, 24, 28, 30, 31, 32, 33, 34, 35, 36, 37, 39, 42, 43, 44, 46],
    "7335_710006": [0, 2, 6, 7, 12, 13, 14, 15, 16, 17, 18, 20, 21, 22, 23, 25, 26, 27, 29, 38, 40, 41, 45, 47],
    "72_1080627": [7, 12, 13, 18, 19, 23, 30, 33, 38, 42, 44, 46],
    "72_1080628": [3, 5, 6, 10, 16, 21, 36, 39, 40, 43, 45, 47],
    "72_1080697": [0, 8, 9, 11, 14, 22, 25, 26, 31, 32, 37, 41],
    "72_1080629": [1, 2, 4, 15, 17, 20, 24, 27, 28, 29, 34, 35]
}

例如，对于第一条数据 "6977_1081969": [0, 4, 5, 6, 7, 11, 14, 15, 17, 19, 20, 23, 25, 31, 32, 34, 35, 36, 38, 39, 40, 42, 44, 47],来说，它表示商品全sku数据集合数据中所有包含 paramId为 6977，valueId为 1081969这个sku属性，即 成色：全新的数据下标集合为 [0, 4, 5, 6, 7, 11, 14, 15, 17, 19, 20, 23, 25, 31, 32, 34, 35, 36, 38, 39, 40, 42, 44, 47]

此集合的计算过程没什么好说，就是遍历商品全sku数据集合数据创建数组而已，为了方便叙述，这里称此集合为 keyRankMap

计算 Map对象

有了上述 keyRankMap，计算我们想要的那个 Map对象 (称为indexKeyInfoMap)也就有了前提条件，

indexKeyInfoMap集合的组成前面已经说过了，类似于一个缓存数据，列举了所有任意个 sku组合的信息，所以那就涉及到一个算法了：

现有 m个数组，数组都不为空，从这些数组中共取 n(n <= m)个数，共有多少种取法？规定，每个数组最多只能取一次，每次最多取一个项

这个算法实际上就是另外一个更加常见的算法的增强版，即 从 m 个数中取 n 个数，共有多少种取法，这里的 m个数可以看成是一个数组，也就是从一个长度为 m的数据中取 n个数，但是现在不是从一个数组中了，而是从 m个数组中取

这个算法当然有很多种写法，只要能达到目的并且效率别太差就行：

/**
 * 给定 mArr长度个数组，从这些数组中取 n 个项，每个数组最多取一项，求所有的可能集合，其中，mArr的每个项的值代表这个数组的长度
 * 例如 composeMArrN(([1, 2, 3], 2))，表示给定了 3 个数组，第一个数组长度为 1，第二个数组长度为 2，第二个数组长度为 3，从这三个数组任意取两个数
 * example： composeMArrN(([1, 2, 3], 2))，返回：
 * [[0,0,-1],[0,1,-1],[0,-1,0],[0,-1,1],[0,-1,2],[-1,0,0],[-1,0,1],[-1,0,2],[-1,1,0],[-1,1,1],[-1,1,2]]
 * 返回的数组长度为 11，表示有1 种取法，数组中每个子数组就是一个取值组合，子数组中的数据项就表示取值的规则
 * 例如，对于上述结果的第一个子数组 [0, 0, -1] 来说，表示第一种取法是 取第一个数组下标为 0 和 第二个数组下标为 0 的数，下标为 2 的数组项值为 -1 表示第三个数组不取任何数
 * @param mArr 数据源信息
 * @param n 取数的个数
 * @param arr 递归使用，外部调用不需要传此项
 * @param hasSeletedArr 递归使用，外部调用不需要传此项
 * @param rootArr 递归使用，外部调用不需要传此项
 */
function composeMArrN (mArr: Array<number>, n: number, arr = [], hasSeletedArr = [], rootArr = []): Array<Array<number>> {
  if (!n || n < 1 || mArr.length < n) {
    return arr
  }
  for (let i = 0; i < mArr.length; i++) {
    // 当前层级已经存在选中项了
    if (hasSeletedArr.includes(i)) continue
    hasSeletedArr = hasSeletedArr.slice()
    hasSeletedArr.push(i)
    for (let j = 0; j < mArr[i]; j++) {
      let arr1 = completeArr(arr, i - arr.length, -1)
      arr1.push(j)
      if (n === 1) {
        arr1 = completeArr(arr1, mArr.length - arr1.length, -1)
        rootArr.push(arr1)
      } else {
        composeMArrN(mArr, n - 1, arr1, hasSeletedArr, rootArr)
      }
    }
  }
  return rootArr
}

其中 completeArr是一个补全数组的辅助方法，比如，对于 [1, 2]这个数组来说，我想把它的长度再增加 3个单位，用 -1来填补多出来的位置，就是调用 completeArr([1, 2], 3, -1)，返回 [1, 2, -1, -1, -1]

以此类推，就能得到当任意取 n个 sku属性时，所组成的 sku组合对应的价格和库存等信息的数据，也就是 indexKeyInfoMap

根据 indexKeyInfoMap 计算出任意状态下 sku 组合对应的信息和置灰信息

indexKeyInfoMap只是一个缓存数据，需要实现的功能是，选中任意 sku数据时，对应的价格和库存等信息，以及应该置灰的 sku信息

例如，对于当选中了 全新-银色这个组合的时候

• 计算对应的价格和库存等信息

全新-银色 是两个 sku属性的组合，则直接在 indexKeyInfoMap中找 key为 1的属性，从其数组值中找匹配 全新-银色，也就是 子key为 6975_730004__6977_1081969的数据项：

其中，priceArr表示所有包含 全新-银色这个 sku组合的 sku数据的价格范围集合，spuDIdArr表示 spuDId集合，totalCount表示总库存

• 计算需要置灰的 sku属性

这才是关键

第一，计算当任何属性都不选的时候，库存为 0的属性；
第二，计算当单独选中 全新 和 单独选中 银色 的时候，分别与这两个属性组合的时候库存为 0的属性；
第三，计算当同时选中 全新-银色的时候，与 全新-银色进行组合的时候库存为 0的属性；

三种情况下应该被置灰的属性的并集就是 当选中 全新-银色的时候，应该被置灰的属性

计算的基础就是 indexKeyInfoMap， 比如对于 第二，计算当单独选中 全新 和 单独选中 银色 的时候，分别与这两个属性组合的时候库存为 0的属性；，其计算过程：

首先，任意一个 sku属性 与全新或 银色组成的组合，就是两个 sku属性链接，长度为 2，所以从 indexKeyInfoMap中选取 key为 1的数据，也就是 indexKeyInfoMap[1]，从此数据中分别找包含 全新 和 银色，也就是 key中包含 6977_1081969 或 6975_730004，并且库存为 0的数据项：

然后再对这被筛选出来的 7条数据进行出来，得到需要被置灰的 sku属性的集合，也就是这些数据的 key字符串中，去掉当前已经选中的 sku属性，即 6977_1081969 和 6975_730004后，还剩下的值的集合

例如，对于 72_1080628__6975_730004而言，其处理之后剩下 72_1080628，即 paramId 为 72， valueId为 1080628的 sku属性所对应的按钮应该被置灰，其他类似

这样就能得到一个数组（需要对数组进行去重），此数组中的每一项，就是在同时选中 全新-银色的时候，所需要置灰不可点的 sku属性按钮

概括成通用解决方案，其实又是一个算法，上面说到过：从 m 个数据中取 n(n <= m) 个数，所有的可能取法，然后再对每种取法进行处理，计算从剩下的 sku属性中取一个与每种取法的 sku组合进行组合时库存为 0的那些 sku属性

/**
 * 从 m 个数字中取 n 个，所有可能的取法（不考虑顺序）
 * @param m 数据总数
 * @param n 取数个数
 * @param arr 递归使用，外部调用不需要传此项
 * @param hasSeletedArr 递归使用，外部调用不需要传此项
 * @param rootArr 递归使用，外部调用不需要传此项
 */
function composeMN (m: number, n: number, arr: number[] = [], hasSeletedArr: number[] = [], rootArr: number[][] = []): number[][] {
  for (let i = 0; i < m; i++) {
    if (hasSeletedArr.includes(i)) continue
    hasSeletedArr = hasSeletedArr.slice()
    hasSeletedArr.push(i)
    let arr1 = arr.slice()
    arr1.push(i)
    if (n !== 1) {
      composeMN(m, n - 1, arr1, hasSeletedArr, rootArr)
    } else {
      rootArr.push(arr1)
    }
  }
  return rootArr
}

当然，你也可以用自己觉得更好的算法，总之能解决问题并且效率及格就行

至此，流程结束，功能完成

算法优化

根据上述流程已经可以实现功能了，效率也不低，正常业务场景使用完全没问题，但还存在一些优化的空间

库存为 0 的单 sku数据缓存

对于一个正常的商品来说，特别是平台直营的商品，在绝大部分情况下，其每一条 sku都应该是有库存的，那么对于这种情况，无论你在什么情况下选中了哪些 sku属性，都不应该出现被置灰的 sku属性，因为所有的 sku都有库存，如果我能确定某个商品所有 sku都有库存，那就无需考虑按钮置灰的事情了，计算量最大的那一部分就完全可以省去了，一下子少了一大半的计算量

如果并不是所有 sku库存都为 0，其实也有优化的空间，可以精确到单个 sku属性，逻辑如下：
遍历所有商品全sku数据集合，找出所有库存为 0的 sku组合，从每个组合中分离出单个 sku属性，将所有的这些单个 sku属性放入一个集合中(称为 emptySkuIncludeList)，那么当用户选中任意 sku组合时，发现用户选中的这些 sku属性全都不在 emptySkuIncludeList这个集合中，那么就可以确定，无论下一个用户点选或取消哪个 sku属性，都不会有需要置灰的 sku属性

这很好理解，比如，现在库存为 0的 sku组合只有 72_1080697__6975_730004__6977_1081969__7335_710006这一条，也就是 版本：日韩、颜色：银色、成色：全新、配置：256G这个 sku组合库存是 0，那么 emptySkuIncludeList也就是 ['72_1080697', '6975_730004', '6977_1081969', '7335_710006']， 当用户点选 sku属性的时候，选了 版本：国行，颜色：金色，对应 id组合也就是 72_1080627 和 6975_730005，发现这两个属性都不在 emptySkuIncludeList中，那么此时就无需预测用户下一步，因为无论用户下一步选中或是取消哪个 sku属性，肯定都不会存在需要置灰的 sku属性

也即，这种情况下，也无需进行置灰 sku属性的计算，同样是少了一大半的计算量

求数组交集

计算 indexKeyInfoMap的时候，比如计算 72_1080627__6975_730003__6977_1080699这个 sku组合对应的 商品全sku数据集合中数据的下标集合，就是从 商品全sku数据集合 中分别查找包含 72_1080627、6975_730003、6977_1080699的下标集合，然后三个集合求交集，就是包含 72_1080627__6975_730003__6977_1080699这个 sku组合的下标集合

一开始我求数组交集，直接就是依次两两比较，遍历其中一个数组，然后查找另外一个数组中有没有包含当前遍历的这个数组项，如果有，那说明就是交集项

const resultArr = []
arr1.forEach(item => {
    if (arr2.includes(item)) {
        // 表明是交集项
        resultArr.push(item)
    }
})

这种算法复杂度大概是 O(m * n)，如果数据量较大，还是比较影响效率的，于是我又想到既然 arr1和 arr2中数据都是升序排列，那么完全可以将算法复杂度降到 O(m)啊，于是有了下面这算法

function intersectionSortArr (...params: Array<Array<number>>): Array<number> {
  if (!params || params.length === 0) return []
  if (params.length === 1) {
    return params[0]
  }
  let arr1 = params[0]
  let arr2 = params[1]
  if (params.length > 2) {
    return intersectionSortArr(arr1, intersectionSortArr(arr2, ...params.slice(2)))
  }
  let arr = []
  if (!arr1.length || !arr2.length || arr1[0] > arr2.slice(-1)[0] || arr2[0] > arr1.slice(-1)[0]) {
    return arr
  }
  let j = 0
  let k = 0
  let arr1Len = arr1.length
  let arr2Len = arr2.length
  while (j < arr1Len && k < arr2Len) {
    if (arr1[j] < arr2[k]) {
      j++
    } else if (arr1[j] > arr2[k]) {
      k++
    } else {
      arr.push(arr1[j])
      j++
      k++
    }
  }
  return arr
}

避免使用模糊度较高的正则表达式

当用户选中一些 sku属性时，需要计算当前状态需要置灰的 sku属性，比如用户选中了 72_1080627 和 6975_730005这两个 sku属性时，按照上面说的，需要到 indexKeyInfoMap[2]里面去找同时包含这两个 sku属性的 sku组合数据

也就是到这些数据里面找：

那么如何从 72_1080627__6975_730003__6977_1080699这种格式的字符串里，找到同时包含 72_1080627 和 6975_730005的那些呢？
一般来说，你可能想到用正则进行匹配，比如我，一开始就拿这个正则表达式去匹配

reg = /[0-9_]*72_1080627[0-9_]*6975_730005[0-9_]*/

为什么这么写呢？因为我只知道按照 paramId进行排序的话，72_1080627是排在 6975_730005前面的，但不清楚 72_1080627和 6975_730005都应该在第几位，前面和后面是否还有其他属性相连，所以写了个很宽泛的正则，一条正则搞定，简单省事

本来写完之后觉得还行，问题不大，后来后端进行极端情况测试的时候，每种商品发了上千条 sku，发现前端会卡十几秒才能动，我赶紧查了一下，发现这块正则耗费了太长时间，就是因为正则太模糊了

优化的方法也很多，比如，你对用户选择 paramId进行位置的确定，明确地知道 72_1080627肯定在第一位，6975_730005肯定在第二位， 并且肯定还有第三个，这样可以将正则精确为

reg = /^72_1080627__6975_730005[0-9_]+/

相比于开始的那种模糊匹配，这种明显精确了很多，少了很多正则分支，但是呢这毕竟还要先确定位置，而且还是会有模糊匹配的情况，最好不用正则

既然选中的一组 sku属性肯定不会有重复的，并且数据都是有序的，也就是位置固定，那么其实就是一个字符串查找嘛，直接 indexOf或者 includes都行，不过呢，这种查找还是会存在一些无效查找，算法复杂度差不多是 O(m * n)这个量级

既然按照 paramId对用户选中的 sku属性进行升序排序，按照顺序组成一个数组，比如 ["72_1080627", "6975_730005"]，然后取 indexKeyInfoMap[2]的每个字符串属性，也按照 sku属性分隔成数组形式，比如 ["72_1080627", "6975_730003", "6977_1080699"]，然后对其遍历：

const skuJoinArr = ["72_1080627", "6975_730003", "6977_1080699"]
const currentSkuArr = ["72_1080627", "6975_730005"]
let i = 0
skuJoinArr.forEach(item => {
    if (item === currentSkuArr[i]) i++
})
if (i === skuJoinArr.length) {
    // 说明匹配
}

无论用户选了哪些 sku属性，我需要查找的 indexKeyInfoMap[index]的属性字符串的长度都只比用户选中的多 1个，并且二者都按照 paramId进行了升序排序，那么只要两个数组按照条件同时步进，最后长度较短的 currentSkuArr能够步进到最后，就说明 skuJoinArr 包含 currentSkuArr

这样算法复杂度就降到了 O(m) 这个量级

当然，肯定还有其他可以优化的地方，我目前比较明显地就做了上面几个，优化这种事情，并不是精确到每一行每一段全项目无死角的彻底优化就是最好的，因为优化过的代码，往往跟按着正常思维写出来的不一样，业务代码讲求一个性价比，均衡发展才是最好的

加了上面的优化之后，再对接后端极限测试，在华为 p30上进行测试，1000多条 sku，只需要 200~300 ms即可完成初始化，600多条sku只需要 70-80ms左右，相比于开始时的十几秒，提升了几十倍

而在实际应用场景中，对于一个正常的商品来说，一般 sku数量不会超过 100条的，比如现在京东上的 iphone XR，也就不到 60条 sku，初始化用时大概 20 ~ 30ms，所以完全够用了

注意事项

上面说到，数据源需要按照 paramId进行排序，一般来说这个字段都会是数字类型（或者数字类型的字符串形式），这里是根据 paramId的大小进行排序的，但这里可能存在一个问题，那就是 js的大数运算
以下参考自 MDN - Number.MAX_SAFE_INTEGER

Javascript有个最大安全整数的概念，此值为 Number.MAX_SAFE_INTEGER，常量值为 9007199254740991，即 2的53次方，这个数字形成的原因是，Javascript 使用 IEEE 754中规定的 double-precision floating-point format numbers，在这个规定中能安全地表示数字的范围在 [-(253 - 1), 253 - 1]。

这里的安全（Safe）是指能够准确地表示整数和正确地比较整数。例如 Number.MAX_SAFE_INTEGER + 1 === Number.MAX_SAFE_INTEGER + 2 将返回 true，这在数学上并不正确。更多参见 Number.isSafeInteger()。

说得明白点，那就是如果 js运算的数字大于 9007199254740991，结果可能就是不准确的，我们这里以后端接口返回的 paramsId 的相互大小来有序化数据，如果 paramsId值的大小超过 9007199254740991，那么两个 paramId之间比较的结果就可能是不对的，如果你已经跟后端确认过了，此值肯定不会超过 9007199254740991，那最好不过，无需任何处理，但如果不能确定，那必然要处理一下的，根据你的实际场景来决定就行

总结

一开始在想思路的时候，我一时半会不知从何下手，因为似乎需要考虑的东西很多，考虑到了这个就忘了那个，但实际上静下心来仔细理清思路后，其实还是比较清晰的，思路有了，再将思路用代码实现出来即可，这个就比较简单了，只要自己不把自己绕晕就行

俗话说 talk is cheap, show me the code，文中一些表达可能还是不太清楚，还是代码最直接，所以我也做了一个在线 Demo（最好在移动端查看），源代码也可以放到 github 上了，感兴趣的可以自己试下

当然了，如果你实在想不明白，也可以把这事丢给后端来做，你调用接口传参数等着接数据也可以（手动狗头）
第一次写那么长的博客，累死我了