R-tree总结

R-tree

R-tree是用来做空间数据存储的树状数据结构。R-tree是B-tree向多维空间发展的另一种形式，并且R树也是平衡树。

R树的核心思想是聚合距离相近的节点并在树结构的上一层将其表示为这些节点的最小外接矩形，这个最小外接矩形就成为上一层的一个节点。因为所有节点都在它们的最小外接矩形中，所以跟某个矩形不相交的查询就一定跟这个矩形中的所有节点都不相交。叶子节点上的每个矩形都代表一个对象，节点都是对象的聚合，并且越往上层聚合的对象就越多。

R树的主要难点在于构建一棵既能保持平衡（所有叶子节点在同一层），又能让树上的矩形既不包括太多空白区域也不过多相交（这样在搜索的时候可以处理尽量少的子树）的高效的树。

1 R-tree数据结构

通常，我们不选择去索引几何物体本身，而是采用最小限定箱 MBB（minimum bounding box) 作为不规则几何图形的 key 来构建空间索引。在二维空间中，我们称之为最小边界矩形MBR(minimum bounding retangle)。叶子节点（leaf node）则存储每个对象需要的数据，一般是一个外接矩形和指向数据的标识符(Index，Obj_ID)。如果是点数据，叶子节点只需要存储这些点本身。如果是多边形数据，一般的做法是在叶子节点中存储多边形的最小外接矩形和指向这个多边形的数据的唯一标识符。而非叶子节点（non-leaf node）上的每一条数据由指向子节点的标识符和该子节点的外接矩形组成(Index，Child_Pointer)。在这里Index表示包围空间数据对象的最小外接矩形MBR。

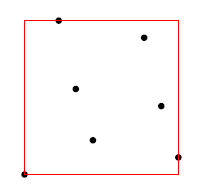
下图是一个MBR的实例，包含了7个点。

通常，只需要两个点就可限定一个矩形，也就是矩形某个对角线的两个点就可以决定一个唯一的矩形。通常使用左下，右上两个点表示或者使用右上，左下两个点来代表这个矩形。判断两个MBR是否相交即判断一个MBR的某个顶点是否处在另一个MBR所代表的范围内。

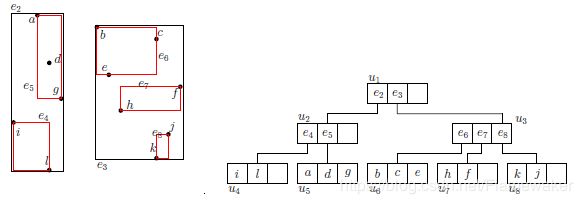
下图是R-tree构造的实例，并假定每个节点限定子节点个数为3。

2 R-tree的搜索

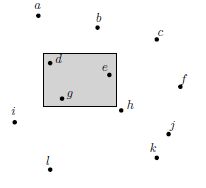
R-tree中的搜索的最常见情况如下，令$S=\{p_1,p_2,...,p_n\}$为$R^2$中的一组点。给定一个与坐标轴平行的矩形Q，范围搜索将返回在S中被Q覆盖的所有点，即$S\cap Q$。如下图所示。该定义可以扩展到任何维度。

2.1 范围搜索

在范围搜索（Range query）中，输入为搜索矩形（查询框），返回与搜索矩形相重叠的实体。

从根节点开始，每个非叶子节点包含一系列外接矩形和指向对应子节点的指针，而叶子节点则包含空间对象的外接矩形以及这些空间对象（或者指向它们的指针）。对于搜索路径上的每个节点，遍历其中的外接矩形，如果与搜索框相交就深入对应的子节点继续搜索。这样递归地搜索下去，直到所有相交的矩形都被访问过为止。如果搜索到一个叶子节点，则尝试比较搜索框与它的外接矩形和数据（如果有的话），如果该叶子节点在搜索框中，则把它加入搜索结果。

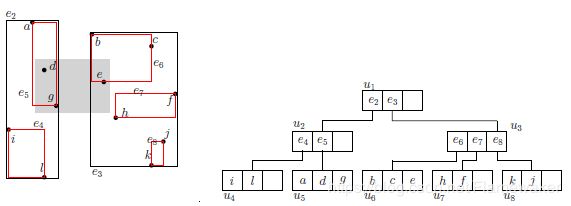
假定Q为我们的搜索范围，R-tree的根节点为root。我们查询的语句为range-query(root; q)。

如下灰色区域是进行的查询Q。节点$u_1,u_2,u_3,u_5,u_6$是查询访问过的节点。

2.2 最近邻搜索

对于最近邻搜索(nearest neighbor search)来说，可以查询一个矩形或者一个点。 先把根节点加入优先队列，然后查询优先队列中离查询的矩形或者点最近的项，直到优先队列被清空或者已经得到要求的邻居数。从优先队列顶端取出每个节点时先将其展开，然后把它的子节点插回优先队列。如果取出的是子节点就直接加入搜索结果。

2.3 knn搜索

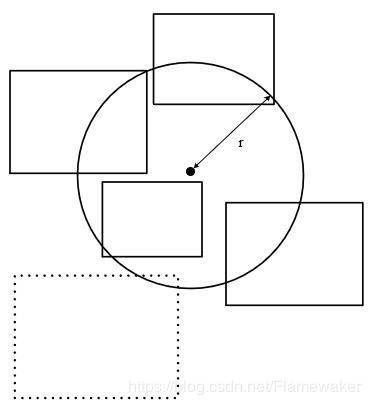
最近邻搜索方法如下。首先利用R-tree的矩形范围搜索方法（boxRangeQuery）粗略估计一个包含不小于k个结果的圆形范围（半径r），利用圆形范围搜索（circleRangeQuery）查找半径（半径r）内的所有点，再对所有得到的结果进行排序。

3 R-tree的插入

通常，R树的构造算法旨在最小化所有MBR的周长或面积总和。

插入节点时，算法从树的根节点开始递归地向下遍历。检查当前节点中所有外接矩形，并启发式地选择在哪个子节点中插入（例如选择插入后外接矩形扩张最小的那个子节点），然后进入选择的那个子节点继续检查，直到到达叶子节点。满的叶子节点应该在插入之前分割，所以插入时到达的叶子节点一定有空位来写数据。由于把整棵树遍历一遍代价太大，在分裂叶子节点时应该使用启发式算法。把新分裂的节点添加进上一层节点，如果这个操作填满了上一层，就继续分裂，直到到达根节点。如果根节点也被填满，就分裂根节点并创建一个新的根节点，这样树就多了一层。

在上图中有几个问题没有解决，R-tree在构造时如何选择需要插入的节点、如何处理节点个数溢出情况。

插入算法首先在树的每一层都要决定把新的数据插入到哪个子树中。经典R树的实现会把数据插入到外接矩形需要面积拓展最小或周长拓展最小的那个子树。一般在选择子树时，如果当前节点N不是叶子结点，则遍历N中的结点，找出添加该数据时扩张最小的结点。如果有多个这样的结点，那么选择面积最小的结点，并继续向下遍历。如下给出选择子树的伪代码：

当下降到叶子节点时，叶子结点的改变信息会向上传递至根结点以改变每个父节点的信息（MBR信息）。在传递变换的过程中，若节点个数溢出情况出现时，R-tree的节点会进行分裂，这时更新上一层的父节点的MBR，并创建指向新生成的节点的指针，如果父节点依旧出现节点个数溢出的情况，则不断向上分割，直到达到根节点。如果根节点也被填满，就分裂根节点并创建一个新的根节点。其伪代码如下：

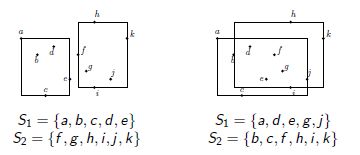
对于分裂操作，我们希望分裂后的节点所形成的MBR的重叠区域尽可能小，也就是得到一个相对最优的空间划分，尽可能满足MBR的拓展最小，并且分裂出的节点分布均匀（在这里令分裂的每个部分的最小个数为原始个数B的0.4，即满足|S1|>=0.4B and |S2| >= 0.4B）。其示意图如下，显然左边的更好。

分裂操作补充：对于所有条目中的每一对E1和E2，计算可以包裹着E1，E2的最小限定框J=MBR(E1, E2) ，然后计算增量d=J-E1-E2。计算结束后选择d最大的一对（即增量最大）（如果d较大，说明挑选出来的两对条目基于对角线离得比较远，这样的好处就是分裂后的两个分组可以尽量不重叠）。

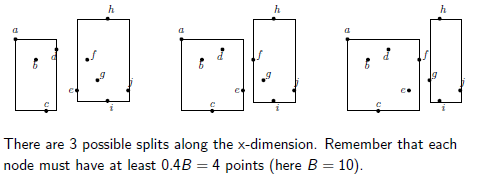
如下给出叶子节点分裂的伪代码：

其示例如下：

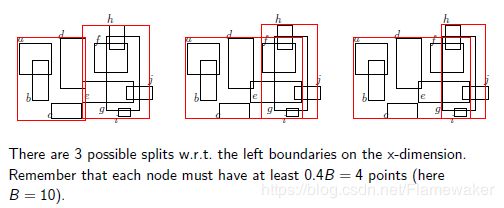
非叶子节点分裂与上面类似，只不过是对MBR的坐标进行排序，如下是非叶子节点分裂的伪代码：

其示例如下：

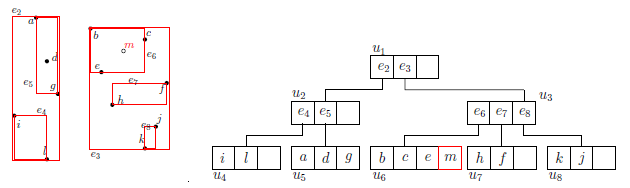
如下给出一个节点插入的例子。假如我们希望将点m插入到R-tree中（假定节点所能容纳的最大个数B=3）。首先将点m插入到叶子节点u6中。

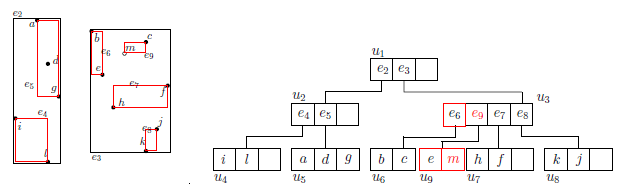
这时发现叶子结点个数发生了溢出，因此将其进行分裂，并向上进行更新操作。将u6分裂成了u6和u9，父节点u3添加指向u9的指针。

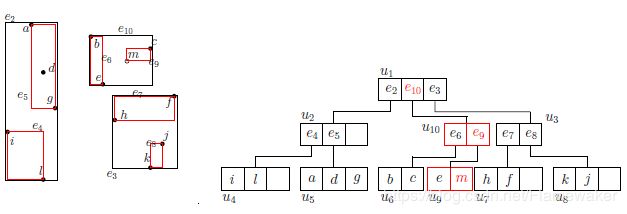
结果节点个数还是发生了溢出，因此对非叶子节点u3进行分裂得到u10。最后更新根节点。

4 R-tree的删除

R树的删除操作与B树的删除操作会有所不同，不过同B树一样，会涉及到压缩等操作。B树删除过程中如果出现结点的记录数少于半满（即下溢）的情况，会两个相邻结点合并。然而R树却是直接重新插入。其主要思想是，若要将一条记录从R-tree中删除，首先在R-tree中找到包含该记录的叶子节点。如果叶子结点的条目数过少（小于要求的最小值m，即发生下溢），则必须将该叶子结点从树中删除。经过这一删除操作，叶子结点中的剩余条目必须重新插入树中（先插入到链表中等待）。此操作将一直重复直至到达根结点（原来属于叶子结点的条目可以使用Insert操作进行重新插入，而那些属于非叶子结点的条目必须插入删除之前所在层的结点，以确保它们所指向的子树还处于相同的层）。同样，调整在此修改树的过程所经过的路径上的所有结点对应的MBR大小。

Delete
描述：将一条记录E从指定的R树中删除。
D1：[找到含有记录的叶子结点] 使用FindLeaf方法找到包含有记录E的叶子结点L。如果搜索失败，则直接终止。
D2：[删除记录] 将E从L中删除。
D3：[传递记录] 对L使用CondenseTree操作
D4：[缩减树] 当经过以上调整后，如果根结点只包含有一个孩子结点，则将这个唯一的孩子结点设为根结点。

FindLeaf
描述：根结点为T，期望找到包含有记录E的叶子结点。
FL1：[搜索子树] 如果T不是叶子结点，则检查每一条T中的条目F，找出与E所对应的矩形相重合的F（不必完全覆盖）。对于所有满足条件的F，对其指向的孩子结点进行FindLeaf操作，直到寻找到E或者所有条目均以被检查过。
FL2：[搜索叶子结点以找到记录] 如果T是叶子结点，那么检查每一个条目是否有E存在，如果有则返回T。

CondenseTree
描述：L为包含有被删除条目的叶子结点。如果L的条目数过少（小于要求的最小值m），则必须将该叶子结点L从树中删除。经过这一删除操作，L中的剩余条目必须重新插入树中。此操作将一直重复直至到达根结点。同样，调整在此修改树的过程所经过的路径上的所有结点对应的矩形大小。
CT1：[初始化] 令N为L。初始化一个用于存储被删除结点包含的条目的链表Q。
CT2：[找到父条目] 如果N为根结点，那么直接跳转至CT6。否则令P为N 的父结点，令EN为P结点中存储的指向N的条目。
CT3：[删除下溢结点] 如果N含有条目数少于m，则从P中删除EN，并把结点N中的条目添加入链表Q中。
CT4：[调整覆盖矩形] 如果N没有被删除，则调整EN.I使得其对应矩形能够恰好覆盖N中的所有条目所对应的矩形。
CT5：[向上一层结点进行操作] 令N等于P，从CT2开始重复操作。
CT6：[重新插入孤立的条目] 所有在Q中的结点中的条目需要被重新插入。原来属于叶子结点的条目可以使用Insert操作进行重新插入，而那些属于非叶子结点的条目必须插入删除之前所在层的结点，以确保它们所指向的子树还处于相同的层。

更多可以参考这篇博客：R-tree原理

5 STR-tree的构造

在上面所示的R-tree的数据结构可以看出，R-tree存在着以下的缺点：
（1）建立索引花费的代价高昂：使用传统的插入函数来建立索引树，会涉及到一系列节点的分裂，子节点的重新分布，以及矩形的求交等。
（2）内存空间利用率不高：由于R树索引中每个节点不一定被子节点填满，这导致它的树高有时过大，这在数据量很大时表现的比较明显。
（3）当对索引多次进行插入或者删除的操作后，同层节点间的交叠大。

针对如上的这些缺点，研究者针对数据极少变动的静态环境提出了Packing的思想。如果事先知道被索引的全部数据，可以针对空间对象的空间分布特性按照某些规则进行分组，凡是在同一组的数据节点作为同一父节点的孩子，这样就可以减少节点之间的交叠，优化查询的性能。

Packing-R-tree 的建立算法存在着通式，可以归纳为：
（1）对输入的r个矩形进行预处理，根据某种规则对r个矩形进行分组，使每个分组包含的矩形数目为节点的最大的容量m。
（2）将每个分组作为一个父节点，于是这些分组便可产生$\lceil r/m\rceil$个父节点。
（3）将这些父节点作为输入，递归地调用索引建立过程，向上生成下一层节点。

Sort-Tile-Recusive（STR-tree)是Packing-R-tree的一种形成方式，其主要思想是将数据通过垂直和水平切片（slice）进行分组。

假设数据空间中存在着r个物体，每个节点最多可以容纳的矩形个数是m。首先用大约$\sqrt{r/m}$个垂直的切片分割整个数据，每个切片大概含有$\sqrt{r/m}$数据矩形，其中最后一个切片可能含有的矩形数目少于$\sqrt{r/m}$个，然后对每个切片在横向分割$\sqrt{r/m}$份，使每份大概含有m个数据矩形，每大概m数据矩形的集合并生成一个父节点。当数据矩形的上层父节点全部生成好后，作为新的数据矩形输入，如此递归地生成索引结构，直到根节点。由于STR 索引从全局上根据空间的邻接性对空间数据进行了分组处理，这使它的检索性能是目前空间索引中比较优秀的。

可以看出，当输入矩形为 r 个时它的 STR 索引高度为$\lceil lo{g}_{m}r\rceil$, 除了最后一个slice，所有的节点都被完全填满，这样最大化地利用了空间。