Unity3d培训中Rotation和EularAngles的正确使用方法

Unity3d里面Transfrom关于旋转的变量是rotation，rotation是一个四元数，四元数就应该有四个值。

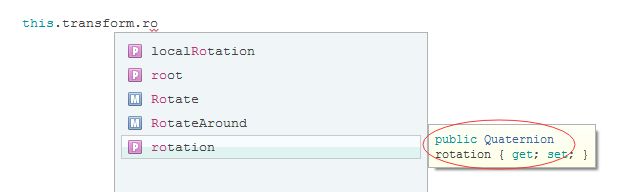
　　但是在编辑器里面，rotation里面只有三个值，这是为啥呢?

　　在Unity里面，一个正面朝上的Plane，他的EularAngles是new vector3(0,0,0)

　　但是当我们把他的EularAngles改成new vector3(-180,-180 ,-180 )的时候，发现他仍旧是正面朝上

　　那我们不用new vector3(-180,-180 ,-180 )，我们用new vector3(-1800,-1800 ,-1800)可不可以，表达正面朝上的角度?也行!

　　所以用Vector3的欧拉角来表示一个角度，可以有千千万万的表示方法!那么我们在计算角度的时候偶尔会把这些重复的角度也计算进去，造成各种各样意向不到的bug和计算错误。这种错误怎么避免呢?聪明的人类引入了一个来自四维空间的数，这个数叫做四元数Quaternion，四元数的最本质是为了解决欧拉角的万向锁和无限自增的问题!

　　下面用一个摄像机跟随来表现一下，使用四元数计算角度在游戏开发过程中相对于欧拉角的优势在哪。

　　如图项目，我们想做一个类似GTA5摄像机跟随的效果，

　　那么第一步，肯定是要记录摄像机的相对位置

　　我们通过摄像机的世界坐标-玩家的世界坐标来获得相对位置。

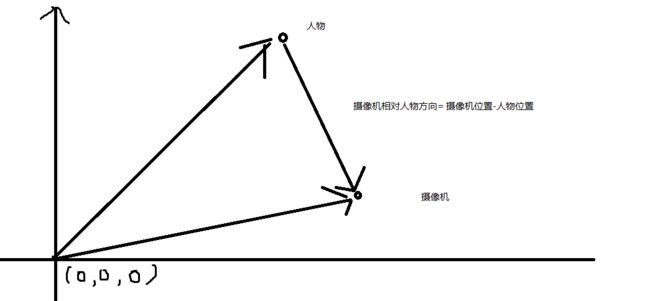
　　那么这样，在每一帧让摄像机的位置，等于主角加方向，在直线上就可以实现摄像机跟随了。

　　但是如果玩家转身了呢?这个相对位置怎么算?

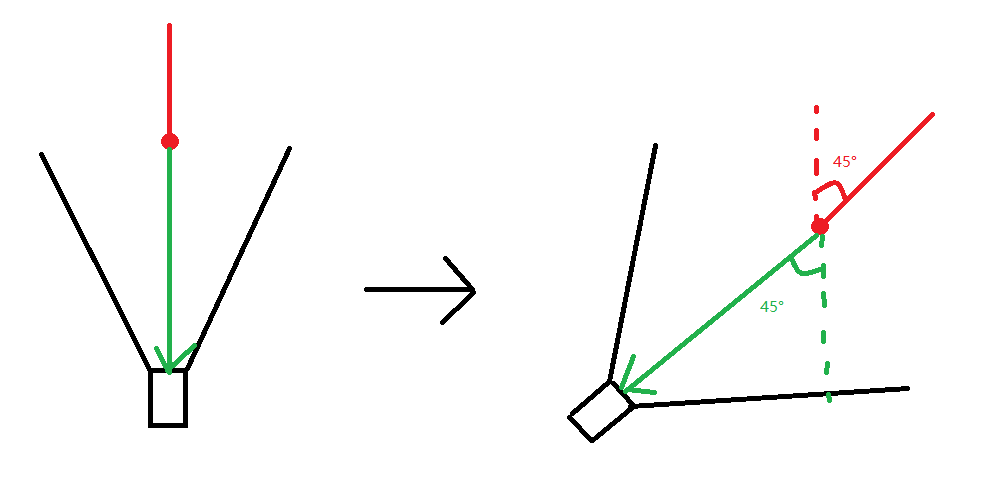
　　由上图我们可以看到转身的过程模拟，其中红色的代表主角，黑色的代表摄像机，虚线表示之前的位置，绿线代表之前算的摄像机相对主角的方向。

　　那么我们可以很清楚的看出来，通常主角模型没有弄错的话，转身基本上都是转Y轴，主角顺时针转了45度，摄像机相对主角的方向向量相对于自身转了

　　45度。所以看似很复杂的问题，其实一点都不负责，我们只要让之前算出来的方向*主角旋转值的四元数就行了。

　　PS：四元数*向量等于旋转之后的向量，不理解原理的话就死记，在3D数学里面是很重要的公式!

using  UnityEngine;
using  System.Collections;
public  class  CameraFollow : MonoBehaviour {
public  GameObject mPlayer;  //获得主角
private  Vector3 m_Dir;  //获得摄像机相对于主角的方向
// Use this for initialization
void  Start () {
m_Dir =  this .transform.position - mPlayer.transform.position;
}
// Update is called once per frame
void  Update () {
this .transform.position = mPlayer.transform.rotation * m_Dir + mPlayer.transform.position; //摄像机的新位置 = 主角位置 + 主角的旋转值 * 摄像机相对于主角的方向
}
}

　　但是我们发现，主角旋转之后，摄像机跟着转了，但是摄像机角度没有更正过来，于是我们接着修改摄像机角度，和上面的一样，主角的旋转值=摄像机的旋转值。于是我们可以直接用欧拉角来赋值，但是一开始摄像机是朝下看的，所以它的旋转值的欧拉角的x轴不为0，但是人物旋转值得x是等于0的，所以我要在最后修改摄像机的旋转值的欧拉角的x轴。

　　(摄像机角度对了，但是方向没转过来)

　　修改后代码：

using  UnityEngine;
using  System.Collections;
public  class  CameraFollow : MonoBehaviour {
public  GameObject mPlayer;  //获得主角
private  Vector3 m_Dir;  //获得摄像机相对于主角的方向
private  float  m_Angle;
// Use this for initialization
void  Start () {
m_Dir =  this .transform.position - mPlayer.transform.position;
m_Angle =  this .transform.eulerAngles.x;
}
// Update is called once per frame
void  Update () {
this .transform.position = mPlayer.transform.rotation * m_Dir + mPlayer.transform.position; //摄像机的新位置 = 主角位置 + 主角的旋转值 * 摄像机相对于主角的方向
this .transform.eulerAngles = mPlayer.transform.eulerAngles;  //摄像机旋转值=主角旋转值
this .transform.eulerAngles =  new  Vector3 (m_Angle,  this .transform.eulerAngles.y,  this .transform.eulerAngles.z);  //让摄像机旋转值的x轴强制位
}
}

　　这样我们就弄出来了最简单的摄像机跟随，但是我们又发现，这种实现效果太简单，和把摄像机拖到主角身上成为子物体没啥两样，于是我们对逻辑进行了优化，让他有个渐变过程。

using  UnityEngine;
using  System.Collections;
public  class  CameraFollow : MonoBehaviour {
public  GameObject mPlayer;  //获得主角
private  Vector3 m_Dir;  //获得摄像机相对于主角的方向
private  float  m_Angle;
// Use this for initialization
void  Start () {
m_Dir =  this .transform.position - mPlayer.transform.position;
m_Angle =  this .transform.eulerAngles.x;
int  a = 6;
int  i = 7;
Debug.Log (a + i++ + i);
}
// Update is called once per frame
void  Update () {
Vector3 pos = mPlayer.transform.rotation * m_Dir + mPlayer.transform.position; //摄像机的新位置 = 主角位置 + 主角的旋转值 * 摄像机相对于主角的方向
this .transform.position = Vector3.Lerp( this .transform.position,pos,Time.deltaTime * 2);  //对位置线性插值
Vector3 angle = mPlayer.transform.eulerAngles;  //摄像机旋转值=主角旋转值
angle.x = m_Angle;
this .transform.eulerAngles = Vector3.Lerp ( this .transform.eulerAngles, angle, Time.deltaTime * 2);  //对旋转值线性插值
}
}

　　我们对计算结果进行线性插值，会发现效果好很多了

　　但是这时候又出来个问题!

　　当旋转值接近360°的时候，他会转1圈回来，造成整个摄像机不受控制。

　　这是为啥呢?

　　原来上面的欧拉角在359 + x 的时候，如果超过360，他会默认变回从0,开始，那么我们的摄像机就会做一个359 -》0的插值，会转倒着一圈回来

　　这就是欧拉角在处理旋转的时候，最容易碰到的头疼的问题，如果我们用四元数，就能完美避开这种情况，因为四元数的世界里面，每个值是匹配一个角度的。

　　不像欧拉角，一个旋转值有无穷种表示方式。

　　于是我们把上面的代码改成四元数计算旋转值得，就能弄出来摄像机跟随的最终版本!

using  UnityEngine;
using  System.Collections;
public  class  CameraFollow : MonoBehaviour {
public  GameObject mPlayer;  //获得主角
private  Vector3 m_Dir;  //获得摄像机相对于主角的方向
private  float  m_Angle;
// Use this for initialization
void  Start () {
m_Dir =  this .transform.position - mPlayer.transform.position;
m_Angle =  this .transform.eulerAngles.x;
int  a = 6;
int  i = 7;
Debug.Log (a + i++ + i);
}
// Update is called once per frame
void  Update () {
Vector3 pos = mPlayer.transform.rotation * m_Dir + mPlayer.transform.position; //摄像机的新位置 = 主角位置 + 主角的旋转值 * 摄像机相对于主角的方向
this .transform.position = Vector3.Lerp( this .transform.position,pos,Time.deltaTime * 2);  //对位置线性插值
Quaternion qua = mPlayer.transform.rotation;  //摄像机旋转值=主角旋转值
this .transform.rotation = Quaternion.Lerp ( this .transform.rotation, qua , Time.deltaTime * 2); //对旋转值线性插值
this .transform.eulerAngles =  new  Vector3 (m_Angle,  this .transform.eulerAngles.y,  this .transform.eulerAngles.z);  //强制固定x轴;
}
}