使用线性回归做客户价值预测
数据统计分析中 y 和 x 的关系
- 线性关系:y = β * x
- 抛物线关系:y = β0 * x + β1 * x^2
- 对数关系:y = ln(x)
- 指数关系:y = e^x
- ...
主要内容
- 线性回归的模型、目标与算法
- 正则化方法:岭回归、LASSO算法、弹性网络
- 算法汇总:最小二乘法、极大似然估计、正则化的最小二乘法
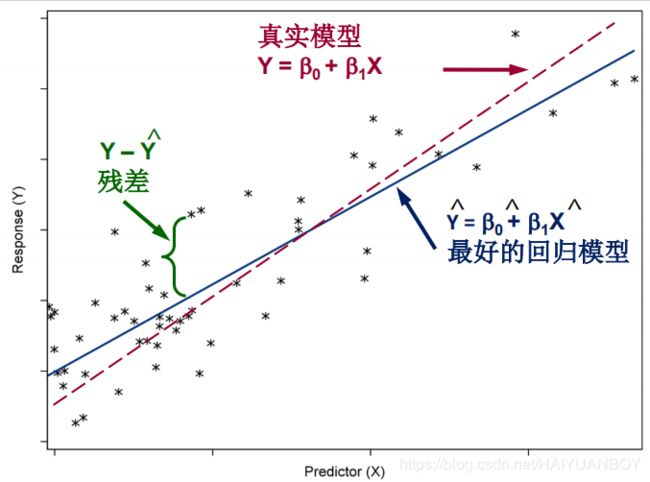
扰动项就是不能被 X 解释的 Y 的变异,就是找不到解释的因素
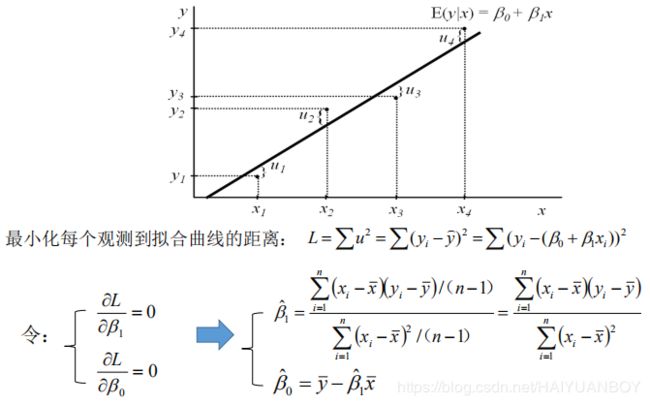
简单线性回归的估计
import matplotlib.pyplot as plt
import os
import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.formula.api import ols
os.chdir(r"D:\pydata")
#pd.set_option('display.max_columns', 8)
# 导入数据和数据清洗
# In[2]:
raw = pd.read_csv(r'creditcard_exp.csv', skipinitialspace=True)
raw.head()
# In[3]:
exp = raw[raw['avg_exp'].notnull()].copy().iloc[:, 2:].drop('age2',axis=1)
exp_new = raw[raw['avg_exp'].isnull()].copy().iloc[:, 2:].drop('age2',axis=1)分出训练集和预测集
lm_s = ols('avg_exp ~ Income', data=exp).fit()
lm_s.summary()
OLS Regression Results
==============================================================================
Dep. Variable: avg_exp R-squared: 0.454
Model: OLS Adj. R-squared: 0.446
Method: Least Squares F-statistic: 56.61
Date: Fri, 26 Apr 2019 Prob (F-statistic): 1.60e-10
Time: 14:10:26 Log-Likelihood: -504.69
No. Observations: 70 AIC: 1013.
Df Residuals: 68 BIC: 1018.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 258.0495 104.290 2.474 0.016 49.942 466.157
Income 97.7286 12.989 7.524 0.000 71.809 123.648
==============================================================================
Omnibus: 3.714 Durbin-Watson: 1.424
Prob(Omnibus): 0.156 Jarque-Bera (JB): 3.507
Skew: 0.485 Prob(JB): 0.173
Kurtosis: 2.490 Cond. No. 21.4
==============================================================================Intercept 就是 β0,Income 就是 β1,y = 258.0495 + 97.7286 * x,这就分析出收入和支出的关系,但我们一般不关心截距 β0,因为可能没法解释(当收入为0时,支出为258.0495),我们关心斜率 β1,这个人的年收入每增加 1 万元,它的月均支出就增加97.7286 元。β1 的解释就是如何是连续变量, x 每增加一个单位,y 增减多少,如果是分类变量,则是有无 x,y 增减多少。但我们要先看 p 值,只有它显著,β1 才有意义,但我们不看 β0 的 p 值,如果不显著就把这个变量给删了,它在模型里没有意义,β0 无论显著不显著都带着
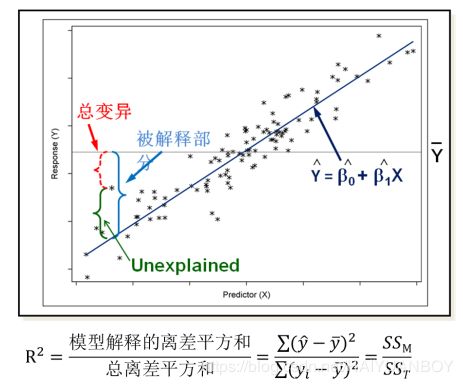
R-squared 描述模型优劣,模型解释力度,45.4%被解释了,越大越好,最大值为 1
Adj. R-squared,是选择模型用的,只有多个模型一起比较才有意义,AIC, BIC 也是如此(更倾向用)
模型评价-拟合优度
做预测
# Predict-在原始数据集上得到预测值和残差(实际值与预测值之差)
# In[8]:
pd.DataFrame([lm_s.predict(exp), lm_s.resid], index=['predict', 'resid']
).T.head()
Out[8]:
predict resid
0 1825.141904 -608.111904
1 1806.803136 -555.303136
3 1379.274813 -522.704813
4 1568.506658 -246.676658
5 1238.281793 -422.251793
lm_s.predict(exp_new)[:5]
Out[9]:
2 1078.969552
11 756.465245
13 736.919530
19 687.077955
20 666.554953
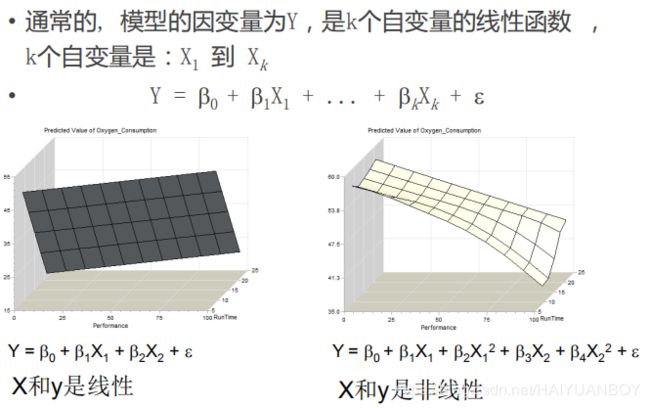
dtype: float64多元线性回归
调整后的R2
多元回归例子
# ### 多元线性回归
# In[10]:
lm_m = ols('avg_exp ~ Age + Income + dist_home_val + dist_avg_income',
data=exp).fit()
lm_m.summary()
OLS Regression Results
==============================================================================
Dep. Variable: avg_exp R-squared: 0.542
Model: OLS Adj. R-squared: 0.513
Method: Least Squares F-statistic: 19.20
Date: Fri, 26 Apr 2019 Prob (F-statistic): 1.82e-10
Time: 15:36:20 Log-Likelihood: -498.59
No. Observations: 70 AIC: 1007.
Df Residuals: 65 BIC: 1018.
Df Model: 4
Covariance Type: nonrobust
===================================================================================
coef std err t P>|t| [0.025 0.975]
-----------------------------------------------------------------------------------
Intercept -32.0078 186.874 -0.171 0.865 -405.221 341.206
Age 1.3723 5.605 0.245 0.807 -9.822 12.566
Income -166.7204 87.607 -1.903 0.061 -341.684 8.243
dist_home_val 1.5329 1.057 1.450 0.152 -0.578 3.644
dist_avg_income 261.8827 87.807 2.982 0.004 86.521 437.245
==============================================================================
Omnibus: 5.234 Durbin-Watson: 1.582
Prob(Omnibus): 0.073 Jarque-Bera (JB): 5.174
Skew: 0.625 Prob(JB): 0.0752
Kurtosis: 2.540 Cond. No. 459.
==============================================================================发现 Age 和 dist_home_val 好像没什么作用,因为 p 值太大了,70个样本,α 选 0.1
由于多个变量 X 之间可能有相关性,可能会导致一些 X 提供的增量信息很少,变得不显著,所以要进行变量筛选,筛选无法提供增量信息的 X
多元线性回归的变量筛选
筛选方法
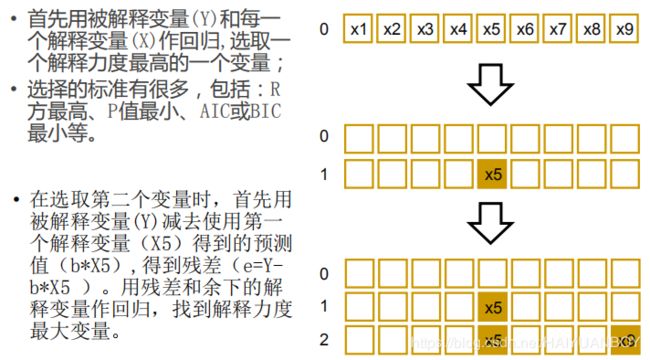
向前选择
# ### 多元线性回归的变量筛选
# In[11]: 向前回归法
'''forward select'''
def forward_select(data, response):
remaining = set(data.columns)
remaining.remove(response)
selected = []
current_score, best_new_score = float('inf'), float('inf')
while remaining:
aic_with_candidates=[]
for candidate in remaining:
formula = "{} ~ {}".format(
response,' + '.join(selected + [candidate]))
aic = ols(formula=formula, data=data).fit().aic
aic_with_candidates.append((aic, candidate))
aic_with_candidates.sort(reverse=True)
best_new_score, best_candidate=aic_with_candidates.pop()
if current_score > best_new_score:
remaining.remove(best_candidate)
selected.append(best_candidate)
current_score = best_new_score
print ('aic is {},continuing!'.format(current_score))
else:
print ('forward selection over!')
break
formula = "{} ~ {} ".format(response,' + '.join(selected))
print('final formula is {}'.format(formula))
model = ols(formula=formula, data=data).fit()
return(model)
# In[12]:
data_for_select = exp[['avg_exp', 'Income', 'Age', 'dist_home_val',
'dist_avg_income']]
lm_m = forward_select(data=data_for_select, response='avg_exp')
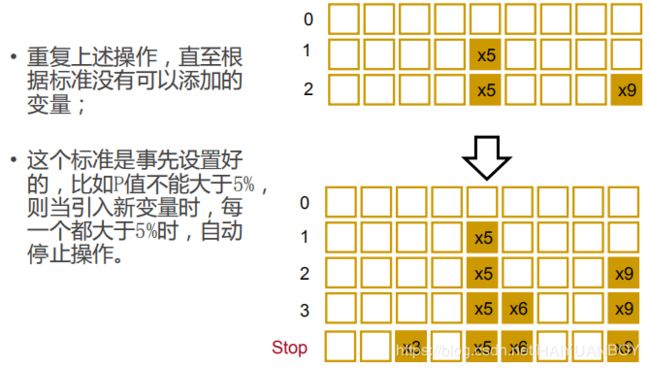
print(lm_m.rsquared)
aic is 1007.6801413968115,continuing!
aic is 1005.4969816306302,continuing!
aic is 1005.2487355956046,continuing!
forward selection over!
final formula is avg_exp ~ dist_avg_income + Income + dist_home_val
0.541151292841195可以看到通过 aic 筛选,并没有筛选去不显著的 dist_home_val
到后面其实我们可以先两两变量相关性检验,然后逐步法变量筛选,决策树或随机森林做模型筛选,再用 IV,最后再整个用逐步法再做一次。决策树做初筛行,但做细筛是不行的,因为他是根据变量覆盖的样本量来做的,不是说 X 对 Y 是否有影响这么做。