数据结构与算法（C++）学习笔记：二叉树（更新完毕）
部分图片非原创，侵删
数据结构与算法（C++）学习笔记：二叉树
- 基本概念
- 存储结构
- 树的存储结构
- 双亲表示法
- 带右兄弟的双亲表示法
- 孩子表示法
- 孩子双亲表示法
- 多重链表法
- 孩子兄弟表示法
- 二叉树的存储结构
- 顺序存储结构
- 二叉链表
- 三叉链表
- 基本操作简介
- 二叉树的遍历
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
- 树的遍历
- 前序遍历
- 后序遍历
- 层序遍历
- 森林的遍历
- 前序遍历
- 后序遍历
- 树、森林与二叉树的转换
- 树->二叉树
- 森林->二叉树
- 二叉树的实现（重难点）
- 二叉树的声明
- 二叉树的关键算法
- 二叉树的创建
- 二叉树的析构
- 二叉树的关键操作
- 二叉树的遍历（二叉链表）
- 前序遍历
- 递归
- 非递归
- 中序遍历
- 递归
- 非递归
- 后序遍历
- 非递归
- 层序遍历
- （重点来啦）答疑+填坑
- QUESTION1
- QUESTION2
- QUESTION3
- 上述操作的完整代码
- 哈夫曼树
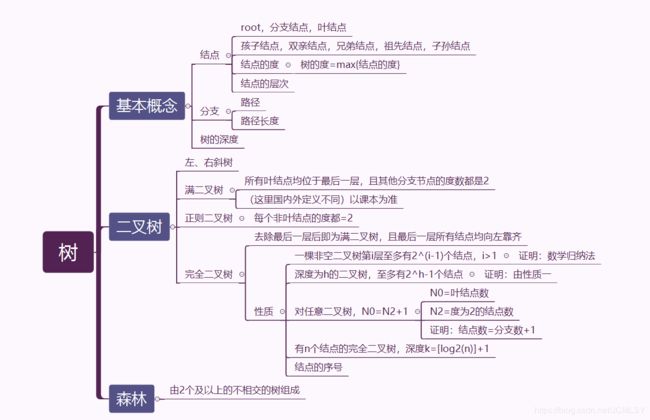
基本概念
树在C++里是一种非常重要的数据结构，应用频率仅次于图。
树在生活中的应用主要有：
- 编译系统：表示源程序的语法结构
- 数据库系统：组织信息，高效查找或检索
- 计算机系统：XML、DOM树、JSON数据、磁盘路径结构
- 文件压缩：Huffman（文章末尾会讲到）
存储结构
树的存储结构
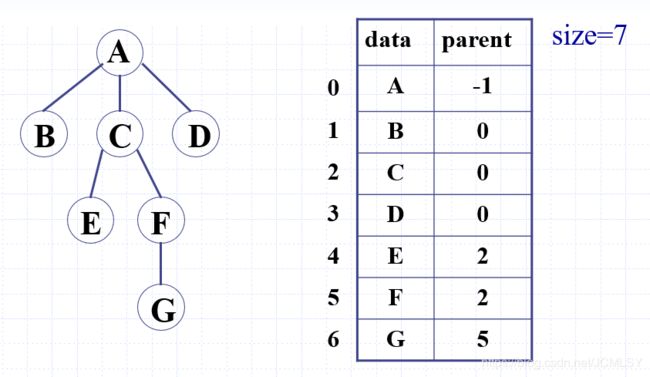
双亲表示法
[数组]
#define MaxSize 100
template<class T>//模板类，可提高代码重用性
struct pNode
{
T data;//此结点存储的数据
int parent;//存储父结点的序号
};
pNode<T>Tree[MaxSize];//此处在使用时应把T换成具体数据类型
int size;
时间复杂度：
- 由叶结点向上搜索根节点：
最好的情况：O(1)
最坏的情况：O(n) 左、右斜树 - 由子结点向上搜索父结点：O(1)
- 从根节点搜索叶结点：O(n)
- 搜索兄弟结点：O(n)
结论：此方法只适用于搜索双亲或根节点
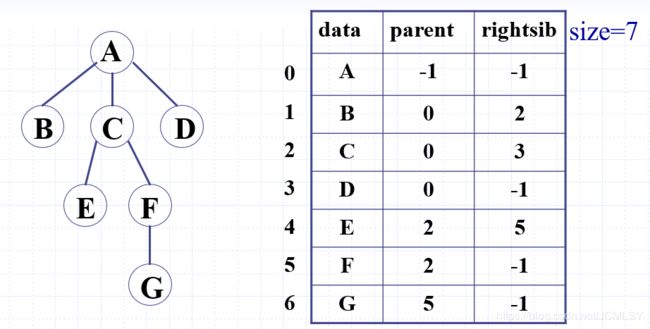
带右兄弟的双亲表示法
[数组]
template<class T>//模板类，可提高代码重用性
struct pNode
{
T data;//此结点存储的数据
int parent, rightbrt;//存储父结点和右兄弟的序号
};
pNode<T>Tree[MaxSize];//此处在使用时应把T换成具体数据类型
int size;
时间复杂度：
- 搜索右兄弟：O(1)
- 搜索孩子结点：O(n)
结论：此方法仅适用于搜索双亲和右兄弟
孩子表示法
//孩子结点
struct CNode
{
int child;//存储数据
CNode *next;//指向下一个孩子结点的指针
};
//表头结点，只与第一个孩子有直接联系
template<class T>
struct CBNode
{
T data;
CNode *firstchild;
};
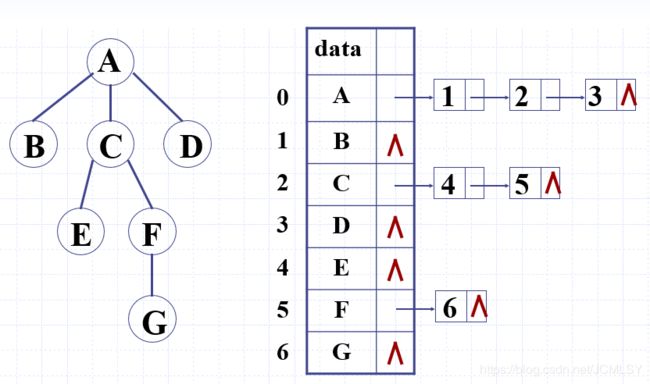
优势：便于搜索孩子结点
弊端：没有孩子的表头结点处，浪费了大量的指针空间；不易从下到上搜索双亲
孩子双亲表示法
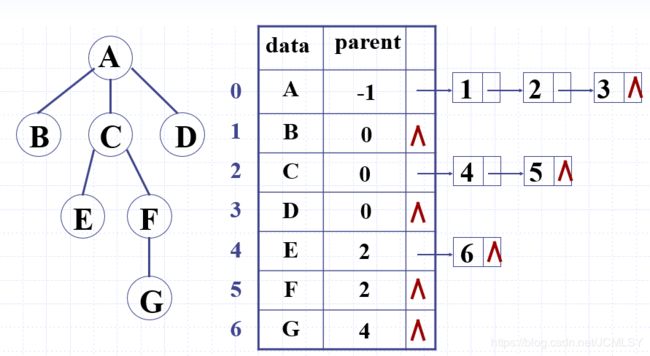
优势：便于寻找双亲和孩子
弊端：利用了顺序表，规模较大
感悟：二叉树更结构平衡，不会有很长的孩子链
多重链表法
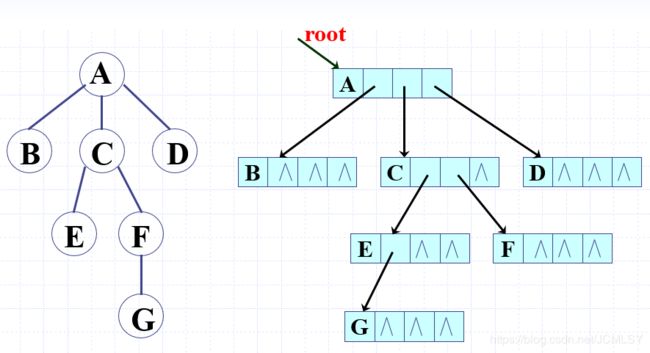
优势：便于查找孩子，逻辑上非常简单粗暴
弊端：首先，效率非常低；其次，每个结点的指针域要选择与树的度已知（结点最大的度），会造成空间的大量浪费
孩子兄弟表示法
template<class T>
struct TNode
{
T data;
TNode<T> *firstchild,*rightbrt;//两个指针分别指向双亲与右兄弟
};
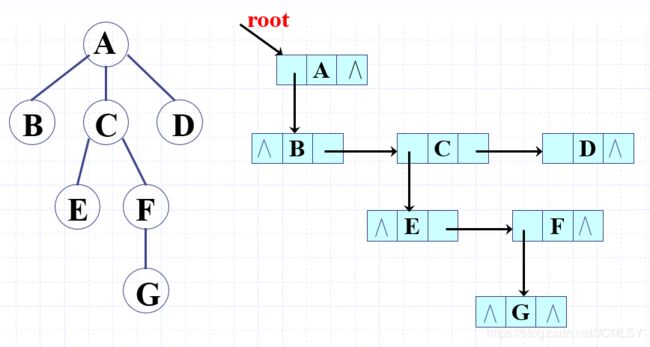
优势：方便搜索孩子与兄弟，是比较好用的一种方法
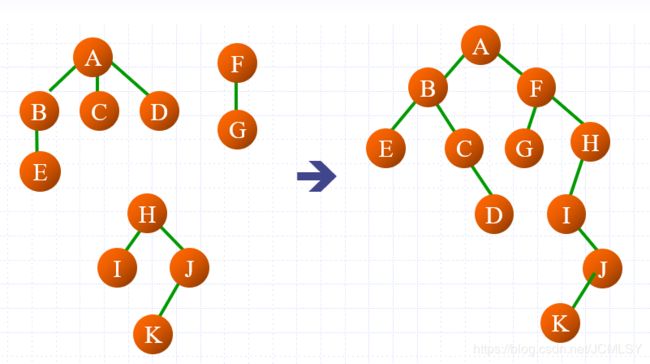
感悟：上边的图片是不是有点眼熟？没错，这不就是把一般的树转化成了二叉树嘛！
二叉树的存储结构
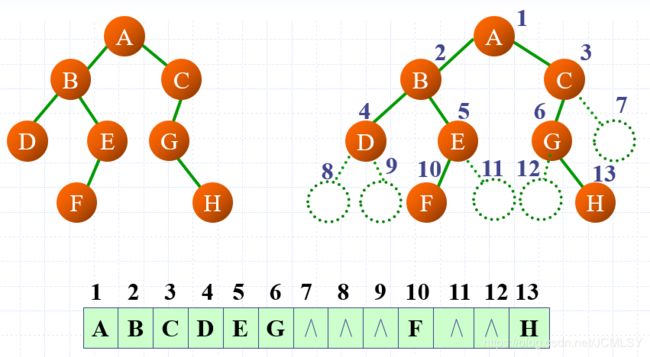
顺序存储结构
方法：
- 将二叉树按照完全二叉树编号
- 用一维数组存储该二叉树
- 无结点的位置也要编号，赋值为NULL
优势：在二叉树结构已知的情况下可以快速搜索
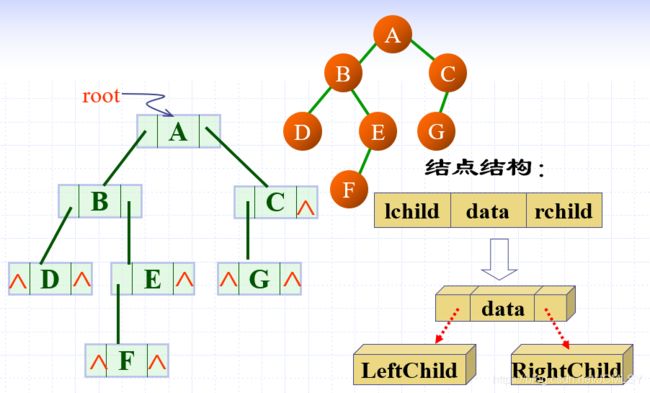
二叉链表
template<class T>
struct Node
{
T data;
Node<T> *lch;
Node<T> *rch;
};
优势：逻辑简单
弊端：很难向上搜索
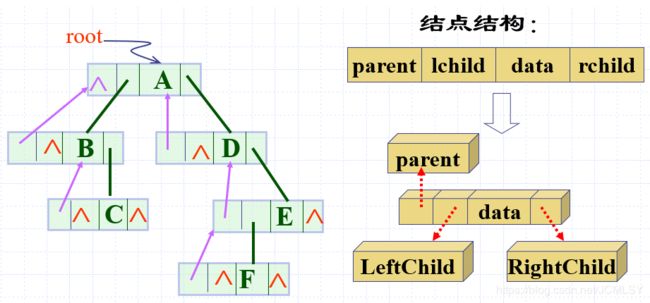
三叉链表
template<class T>
struct Node
{
T data;
Node<T> *parent,*lchild,*rchild;
};
在二叉链表的基础上，加了一个指向双亲的指针，方便向上搜索
基本操作简介
遍历的定义：从根节点出发，按照某种次序依次访问所有结点，且每个结点仅访问一次。
注意体会这里隐含的递归思想。
二叉树的遍历
前序遍历
- 访问根节点 D
- 前序遍历左子树 L
- 前序遍历右子树 R
中序遍历
- 中序遍历左子树 L
- 访问根节点 D
- 中序遍历右子树 R
后序遍历
- 后序遍历左子树 L
- 后序遍历右子树 R
- 访问根节点 D
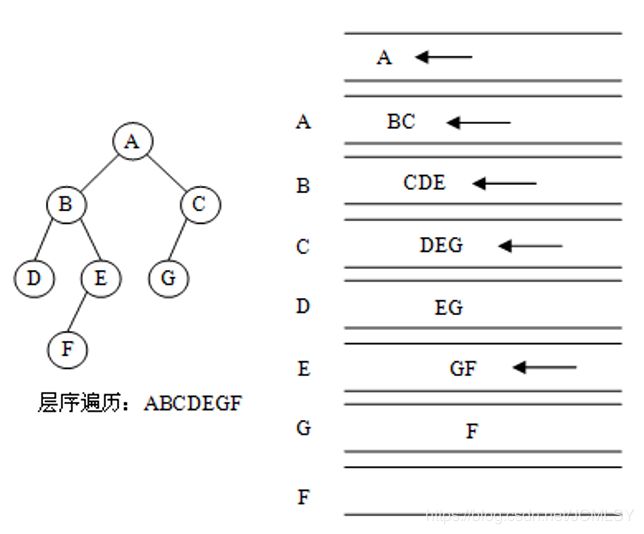
层序遍历
从上到下，从左到右依次遍历。
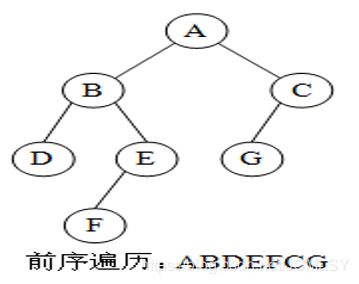
下面来从实例来理解树的遍历方法
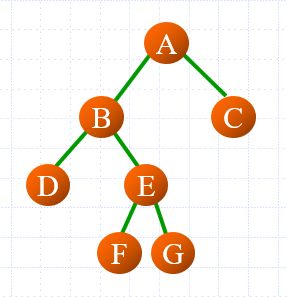
前序遍历 D-L-R： ABDEFGC
中序遍历 L-D-R： DBFEGAC
后序遍历 L-R-D： DFGEBCA
层序遍历（最简单）： ABCDEFG
个人经验：牢记每种遍历方式对应的字母口诀，再套用即可。
重要题型：由两种给出的遍历方式来推理一棵二叉树的结构。
例：已知二叉树的前序序列{ABCDEFGH} 和中序序列 {CDBAFEHG} ，试确定该二叉树的结构。
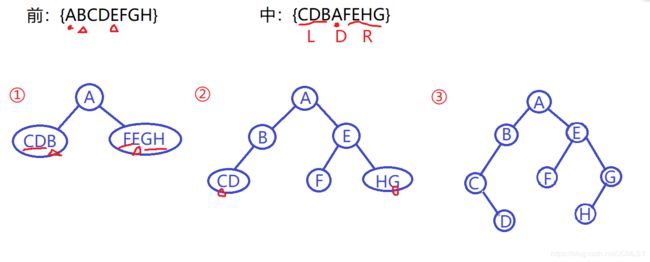
TIP：注意中序遍历左孩子在最前面。（对于各种遍历的组合，解题方法类似）
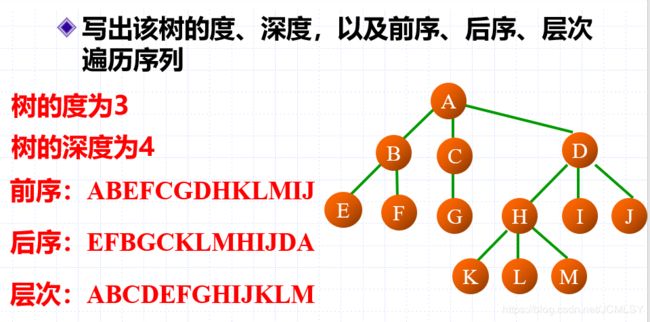
树的遍历
前序遍历
- 访问根节点
- 从左到右遍历各个子树
后序遍历
- 从左到右遍历每一棵子树
- 访问根节点
层序遍历
从上到下，从左到右访问每个结点。
森林的遍历
前序遍历
从左到右前序遍历每个子树。
后序遍历
从左到右后序遍历每个子树。
树、森林与二叉树的转换
树->二叉树
【前面挖的坑这里就填上啦】
利用树的孩子兄弟表示法，即可将一般树转化为二叉树。
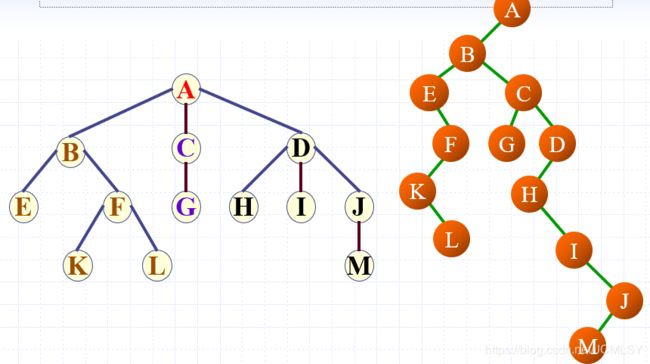
森林->二叉树
- 分别将森林中的每棵树转化为二叉树
- 从左到右连接新的二叉树：后一棵树的根节点是前一棵树根节点的右孩子
二叉树的实现（重难点）
二叉树的声明
template<class T>
struct BiNode//这里采用的是二叉链表法
{
T data;
BiNode<T> *lchild;
BiNode<T> *rchild;
}；
template<class T>
class BiTree
{
private:
void Create(BiNode<T> *&R,T data[],int i，int n)； //创建 思考：这里为什么要用二级指针捏
void Release(BiNode<T> *R);//释放
public:
BiNode<T> *root;//思考：根节点为什么是公有的？
BiTree():root(NULL){} //空树
BiTree(T data[],int n);
void PreOrder(BiNode<T>*R);//前序
void InOrder(BiNode<T>*R);//中序
void PostOrder(BiNode<T>*R);//后序
void LevelOrder(BiNode<T>*R);//层序
~BiTree();
}；
二叉树的关键算法
二叉树的创建
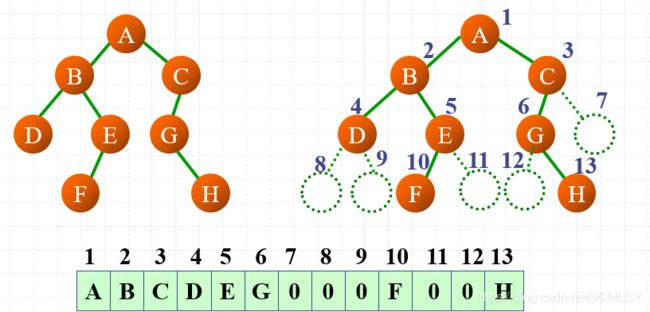
利用顺序存储结构建立二叉链表
由性质5 若当前结点为i，则左孩子为2i，右孩子为2i+1（此处不考虑值是否为零）
基本思想：
- 建立根节点
- 建立左子树
- 建立右子树
template <class T>
void BiTree<T>::Create(BiNode<T>* &R, T data[], int i, int n) //创建二叉树
{ //R当前要建立的根节点指针，i当前根节点编号 n表示最后一个叶子结点的编号
//R的类型：指针的引用
if ((i <= n) && (data[i - 1] != '0'))
{
R = new BiNode<T>; //1、建立根结点
R->data = data[i - 1];
R->lchild = NULL;
R->rchild = NULL;
Create(R->lchild, data, 2 * i, n); //2、建立左子树
Create(R->rchild, data, 2 * i + 1, n);//3、建立右子树
}
}
template<class T>
BiTree<T>::BiTree(T data[],int n)
{
Create(root,data,1,int n);
}
将上述过程可视化
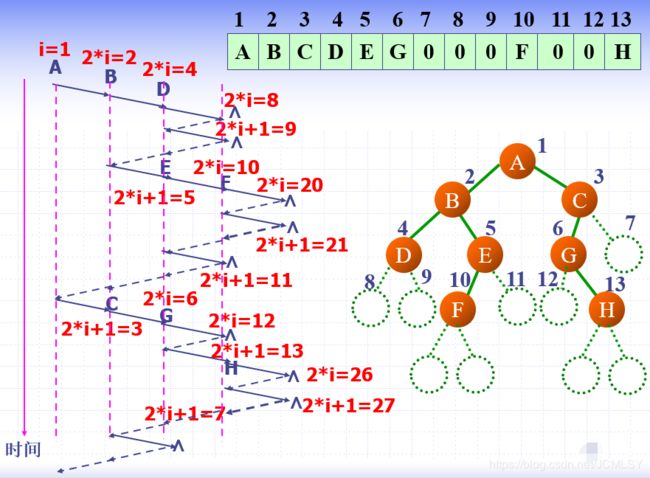
反思：这种方法有一个明显的弊端–会占用大量的空间，这就是为什么我们更愿意使用二叉树。
二叉树的析构
易错点：容易产生内存泄漏
基本思路：采用后序遍历的方法从下到上释放结点空间
template<class T>
void BiTree<T>::Release(BiNode<T> *R)//由于析构函数是不可以有形参的，只能单独写一个函数来释放空间
{
if(R != NULL)
{
Release(R->lchild);
Release(R->rchild);
delete R;
}
}
template<class T>
BiTree<T>::~BiTree()
{
Release(root);
}
PS：由于析构函数对于一棵树只运行一次，所以在这里使用递归并不会对程序的效率产生太大影响。但是递归的使用，对下面要介绍的遍历操作来说，影响就十分严重了。
二叉树的关键操作
二叉树的遍历（二叉链表）
前序遍历
递归
template<class T>
void BiTree<T>::PreOrder(BiNode<T> *Root)
{
if(Root != NULL)
{
cout<<Root->data;//结点
PreOrder(Root->lchild);//左子树
PreOrder(Root->rchild);//右子树
}
}
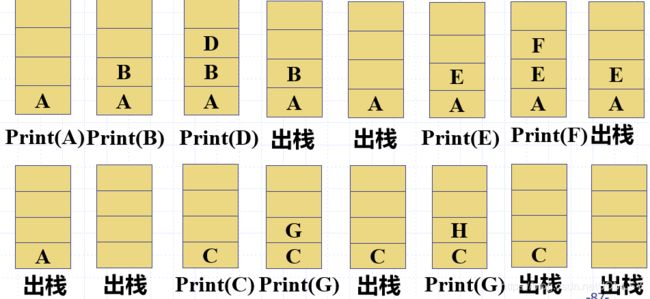
递归过程可视化：
（在这里结合了栈的思想）
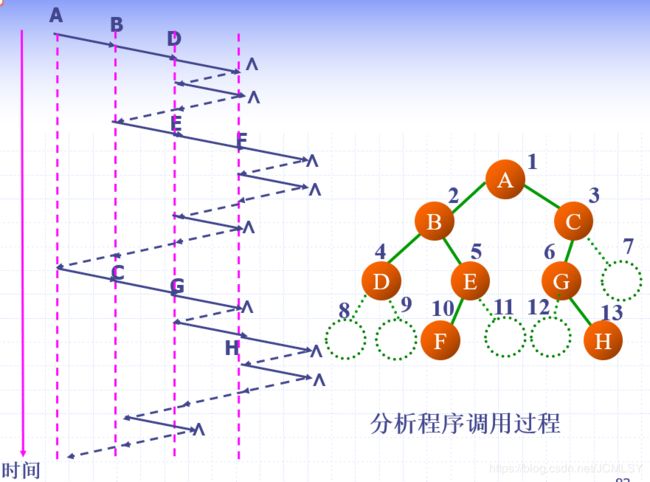
反思：在遍历的整个过程中，会涉及大量的入栈、出栈操作，再加上这一操作是用递归来实现的，回使程序的运行非常低效。
思考：对于树而言，遍历是经常使用的操作，不可能只用递归来实现。那么有没有什么更好的方法呢？
非递归
所有的递归函数都可以改写为效率较高的非递归函数。
对于二叉树的遍历操作，只要找出遍历的结点入栈、出栈
打印的规律，就可以了解递归遍历的全过程。但是当函数调用结束以后，如何区分是左子树还是右子树呢？
基本思想：
- 利用一个简单的标记，规定：整型数据为1-左子树，2-右子树。
第一次迭代优化：递归->非递归
伪代码：（栈顶元素永远为当前结点的父结点）
（1） 若R != NULL，访问R并入栈，调用 R=R->lchild (设R标记为1)返回（1）
（2） 若R==NULL，重新设 R=栈顶元素
（2.1） 若R标记为2，说明右子树返回，R出栈，重新设R=栈顶元素，返回（2.1）
（2.2） 若R标记为1，说明左子树返回，调用 R=R->rchild（设R标记为2），返回（1）
（反复执行至 栈空&&当前结点=NULL）
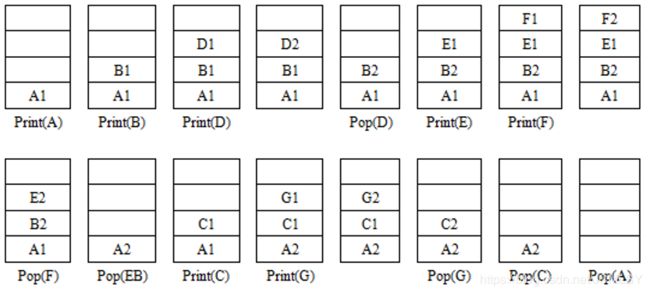
在这里我们先定义一个栈中的结点元素
template<class T>class SNode
{
public:
BiNode<T> *R;
int tag;
}；
PS：使用顺序栈–结点数组
前序遍历函数（这里的形参又变成了一级指针）
template<class T>
void BiTree<T>::PreOrder(BiNode<T> *R)
{
SNode<T> S[100]; //栈
int top = -1; //栈顶指针
do
{
while(R != NULL) //入栈，访问左子树
{
S[++top].R = R;
S[top].tag = 1; //标记为1
cout<<R->data;
R = R->lchild;
}
while((top != -1)&&(S[top].tag == 2)) top--; //出栈
if((top != -1)&&(S[top].tag == 1)) //访问右子树
{
R = S[top].R->rchild;
S[top].tag = 2;//设置栈顶标记
}
}while(top != -1);
}
思考：是否可以进一步优化呢？
**分析：**对于当前结点，当访问玩它的左子树以后，需要依靠它找到它的右子树，此后当前结点就可以不再提供任何信息了，只需要静静的等待出栈。所以，让当前结点提前出栈，就可以简化非递归过程。
这就需要栈：
- 保存当前结点
- 访问当前结点的左子树
- 访问当前节点左子树，当前结点出栈
- 访问其右子树
第二次迭代优化：
template<class T>
void BiTree<T>::PreOrder(BiNode<T> *R)
{
BiNode<T> S[100];
int top = -1;
while((top != -1)||(R != NULL))
{
if(R != NULL)
{
cout<<R->data; //访问
S[++top] = R; //入栈
R = R->lchild;
}
else
{
R = S[top--]; //当前结点出栈
R = R->rchild; //访问当前结点的右孩子
}
}
}
**总结：**优化以后的非递归算法在空间与时间上都提高了效率，对于一棵有n个结点的二叉树，其前序遍历的时间复杂度为O(nlog n).
中序遍历
递归
template<class T>
void BiTree<T>::InOrder(BiNode<T> *Root)
{
if(Root != NULL)
{
InOrder(Root->lchild);//左子树
cout<<Root->data;//结点
InOrder(Root->rchild);//右子树
}
}
非递归
此处的分析方法与前序遍历相同，唯一的区别就是结点的访问顺序变成了L-D-R
第一次迭代优化：递归->非递归
伪代码：（栈顶元素永远为当前结点的父结点）
（1）若R != NULL，R入栈，调用 R=R->lchild（设R标记为1） 返回（1）
（2）若 R==NULL，重新设 R=栈顶元素
（2.1）若R标记为2，说明右子树返回，R出栈，重新设R=栈顶元素，返回（1）
（2.2）若R标记为1，说明左子树返回，访问R，并调用 R=R->rchild（设R标记为2），返回（1）
反复执行上述操作直到栈空
template<class T>
void BiTree<T>::InOrder(BiNode<T> *R)
{
SNode<T> S[100]; //栈
int top = -1; //栈顶指针
do
{
while(R != NULL) //入栈，设置遍历左子树
{
S[++top].R = R;
S[top].tag = 1;
R = R->lchild;
}
while((top != -1)&&(S[top].tag == 2)) top--; //出栈
if((top != 1)&&(S[top].tag == 1)) //访问栈顶元素
{ //遍历右子树
cout<<S[top].R->data;
R = S[top].R->rchild;
S[top].tag = 2;
}
}while(top != -1);
}
第二次迭代优化：
template<class T>
void BiTree<T>::InOrder(BiNode<T> *R)
{
BiNode<T> S[100];
int top = -1;
while((top != -1)||(R != NULL))
{
if(R != NULL)
{
S[++top] = R; //入栈
R = R->lchild;
cout<<R->data; //访问
}
else
{
R = S[top--]; //当前结点出栈
R = R->rchild; //访问当前结点的右孩子
}
}
}
后序遍历
template<class T>
void BiTree<T>::PostOrder(BiNode<T> *Root)
{
if(Root != NULL)
{
PostOrder(Root->lchild);//左子树
PostOrder(Root->rchild);//右子树
cout<<Root->data;//结点
}
}
非递归
第一次迭代优化：递归->非递归
伪代码：（栈顶元素永远为当前结点的父结点）
（1）若R != NULL，R入栈，调用 R=R->lchild（设R标记为1） 返回（1）
（2）若 R==NULL，重新设 R=栈顶元素
（2.1）若R标记为2，说明右子树返回，R出栈，重新设R=栈顶元素，返回（1）
（2.2）若R标记为1，说明左子树返回，访问R，并调用 R=R->rchild（设R标记为2），返回（1）
反复执行上述操作直到栈空
template<class T>
void BiTree<T>::PostOrder(BiNode<T> *R)
{
SNode<T> S[100];
int top= -1;
do
{
while(R != NULL)
{
S[++top].R = R;
S[top].tag = 1;
R = R->lchild;
}
while((top != -1)&&(S[top].tag == 2))
{
cout<<S[top].R->data;
top--;
}
if((top != 1)&&(S[top].tag == 1))
{
R = S[top].R->rchild;
S[top].tag = 2;
}
}while(top != -1);
}
思考：后序遍历的非递归算法还能优化吗？
答案是不能，因为对于后序排列来说，双亲结点会在孩子结点后被访问，无法提前出栈。
层序遍历
层序遍历的基本思想是先入先出，显然，我们用队列来实现这一操作。
伪代码：
- 若根节点非空，入队；
- 若队列不空：
2.1 队头元素出队
2.2 访问该元素
2.3 若该结点的左孩子非空，则左孩子入队
2.4 若该结点的右孩子非空，则右孩子入队
PS：这里同样用的是顺序队列–结点数组
层序遍历函数
template<class T>
void BiTree<T>::LevelOrder(BiNode<T> *R)
{
BiNode<T> *queue[MAXSIZE];
int f=0,r=0; //初始化空队列
if(R != NULL)
queue[++r] = R;//根结点入队
while(f != r)
{
BiNode<T> *p=queue[++f];//队头元素出队
cout<<p->data;//出队打印
if(p->lchild != NULL)
queue[++r] = p->lchild;//左孩子入队
if(p->rchild != NULL)
queue[++r] = p->rchild;//右孩子入队
}
}
（重点来啦）答疑+填坑
我们在上面的操作实现中，提出了以下三个问题
QUESTION1: 在声明中为什么不用构造函数和析构函数实现树的创建和删除？
QUESTION2：为什么root结点要设置为公有成分？
QUESTION3：[难]为什么构造树时，形参要用二级指针？
QUESTION1
为什么不用构造函数直接创建树？
我个人认为是为了操作更方便，逻辑上比较清晰。这样在主函数调用的时候只用传两个参数，不用自己添加结点指针。
为什么不用析构函数删除树？
基本功，因为析构函数是不能有参数的。
QUESTION2
为什么root结点要设置为公有成分？
这个问题大家只需要认认真真自己敲一遍代码就会懂啦（我就是），因为调用遍历函数的时候需要传一个指向根结点的指针，如果root是私有的，就没办法找到树的根结点了。
QUESTION3
为什么构造树时，形参要用二级指针？
这里请参考一位大佬的文章
涉及到变量的修改权限问题。
上述操作的完整代码
递归版，一级优化版，二级优化版 请移步Github
哈夫曼树
这部分内容比较多，于是我新写了一篇文章。欢迎大家阅读。
作为初学者，我个人的编程能力还不够强，大家如果上述内容有疑问，可以直接评论或私信我哦。
祝同学们学习进步哈哈