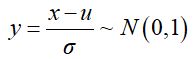数据预处理之数据无量纲化(标准化/归一化)
在进行特征选择之前,一般会先进行数据无量纲化处理,这样,表征不同属性(单位不同)的各特征之间才有可比性,如1cm 与 0.1kg 你怎么比?无量纲处理方法很多,使用不同的方法,对最终的机器学习模型会产生不同的影响。本文将对常用的无量纲化技术进行总结,试图指出他们的适用场景,并给出在Python中的相应调用方式。正文中每列代表一个 属性/特征,每行表示一个/条 样本。
1. min-max归一化
该方法是对原始数据进行线性变换,将其映射到[0,1]之间,该方法也被称为离差标准化(但是请注意,网上更多人喜欢把z-score称为标准化方法,把min-max称为归一化方法,然后在此基础上,强行给标准化(z-score)与归一化(min-max)划条界线,以显示二者之间的相异性。对!二者之间确实有很大的不同,这个我们后面会有介绍,但是这两个方法说到底还都是用来去除量纲的,都是无量纲化技术中的一员而已,所以,请不要纠结标准化与归一化这两个概念了)。
上式中,min是样本的最小值,max是样本的最大值。由于最大值与最小值可能是动态变化的,同时也非常容易受噪声(异常点、离群点)影响,因此一般适合小数据的场景。此外,该方法还有两点好处:
1) 如果某属性/特征的方差很小,如身高:np.array([[1.70],[1.71],[1.72],[1.70],[1.73]]),实际5条数据在身高这个特征上是有差异的,但是却很微弱,这样不利于模型的学习,进行min-max归一化后为:array([[ 0. ], [ 0.33333333], [ 0.66666667], [ 0. ], [ 1. ]]),相当于放大了差异;
2) 维持稀疏矩阵中为0的条目。
使用方法如下:
from sklearn.preprocessing import MinMaxScaler
x = np.array([[1,-1,2],[2,0,0],[0,1,-1]])
x1 = MinMaxScaler().fit_transform(x)不难发现,x1每列的值都在[0,1]之间,也就是说,该模块是按列计算的。并且MinMaxScaler在构造类对象的时候也可以直接指定最大最小值的范围:scaler = MinMaxScaler(feature_range=(min, max)).
2. z-score标准化
z-score标准化(zero-mena normalization,0-均值标准化)方法的公式如下所示:
上式中,x是原始数据,u是样本均值,σ是样本标准差。回顾下正态分布的基本性质,若x~N(u,σ^2),则有
于是,可以看出,z-score标准化方法试图将原始数据集标准化成均值为0,方差为1且接近于标准正态分布的数据集。然而,一旦原始数据的分布 不 接近于一般正态分布,则标准化的效果会不好。该方法比较适合数据量大的场景(即样本足够多,现在都流行大数据,因此可以比较放心地用)。此外,相对于min-max归一化方法,该方法不仅能够去除量纲,还能够把所有维度的变量一视同仁(因为每个维度都服从均值为0、方差1的正态分布),在最后计算距离时各个维度数据发挥了相同的作用,避免了不同量纲的选取对距离计算产生的巨大影响。所以,涉及到计算点与点之间的距离,如利用距离度量来计算相似度、PCA、LDA,聚类分析等,并且数据量大(近似正态分布),可考虑该方法。相反地,如果想保留原始数据中由标准差所反映的潜在权重关系应该选择min-max归一化,基于数学角度的解释可参阅这两篇博文[1,2],链接在最下方reference内。
from sklearn.preprocessing import StandardScaler
x = np.array([[1,2,3],[4,5,6],[1,2,1]])
x1 = StandardScaler().fit_transform(x)可以发现,x1的每一列加起来都是0,方差是1左右。注意该方法同样按列(即每个属性/特征)进行计算。并且StandardScaler类还有一个好处,就是可以直接调用其对象的.mean_与.std_方法查看原始数据的均值与标准差。
X = np.array([[ 1., -1., 2.], ... [ 2., 0., 0.], ... [ 0., 1., -1.]])
scaler = StandardScaler().fit(X)
scaler.mean_
array([ 1. ..., 0. ..., 0.33...])3. Normalization
在一些地方,有人把这种方法翻译为正则化,但是机器学习中的正则化更多是与模型相关(比如逻辑回归在损失函数后增加L2正则项),所以这种翻译我不喜欢;也有人称之为归一化,但是吧,有时这种方法并没体现“归一”特性,如处理后的数据该是负号的还是负号;直译表示标准化吧,我怕你们又把这种方法与z-score标准化联系起来,因此,就不翻译了吧。
其实这个方法是根据范数来进行 Normalization的,何为范数?听着感觉高大上,其实非常常见。Lp-范数的计算公式如下所示:
可见,L2范数即为欧式距离,则规则为L2的Normalization公式如下所示,易知,其将每行(条)数据转为相应的“单位向量”。
Normalization的过程是将每个样本缩放到单位范数(结合单位向量进行理解,p=2时为单位向量,其他为单位范数),如果后面要使用如二次型(点积)或者其它核方法计算两个样本之间的相似性这个方法会很有用[3]。
from sklearn import preprocessing
normalizer = preprocessing.Normalizer().fit(X)
normalizer.transform(X)reference
[1]. 《再谈机器学习中的归一化方法(Normalization Method)》
[2]. 《归一化与标准化》
[3]. 《关于使用sklearn进行数据预处理 —— 归一化/标准化/正则化》