【编译原理学习笔记】3：正规式,正规集,确定的/不确定的有穷自动机

以后*都表示前一个元素的闭包，就当写在了右上角。

正规式和正规集

3型文法(正规文法)所描述的正是终结符集上的正规集，而正规式(正则表达式)就是一种表示正规集的工具。

正规式可以是ε和Φ，对应的正规集是{ε}和{Φ}，还可以是终结符经过有限次闭包、或(要放到括号里)、连接得到的。正规式e表示的正规集记作L(e)。

当两个正规式所表示的正规集相同时，则两个正规式等价。如：

(a|b)*=(a*b*)*
b(ab)*=(ba)*b

从正规式得到正规文法

形如A->xy的正规式，变成：

A->xB
B->y

形如A->x|y的正规式，变成：

A->x
A->y

形如A->r*的正规式，变成：

A->rB
A->ε
B->rB
B->ε

从正规文法得到正规式

基本还是做上面的逆变换，还会用到一些正规式的代数规律变换，注意文法A->xA|y可以直接变成正规式A=x*y。

确定的有穷自动机(DFA)

有穷自动机(FA)可以作为一种识别正规集的装置。确定的有穷自动机可以表示成一个五元组：
$$M=(K,\Sigma ,f,S,Z)即(状态集,字母表,映射,唯一开始状态,终止集合)$$
其中状态集就是DFA所走到的各个状态结点名，字母表则是所有出现在状态转移弧上的字母。前者对应了那些非终结符，后者对应着终结符或者ε(无条件的转移)。

DFA中开始状态S只有一个；终止状态(可接受状态)则可能不唯一，都在集合Z中；状态转换函数f是一个单值函数，即在一个状态上给出一个输入符号只能到达唯一的下一状态。

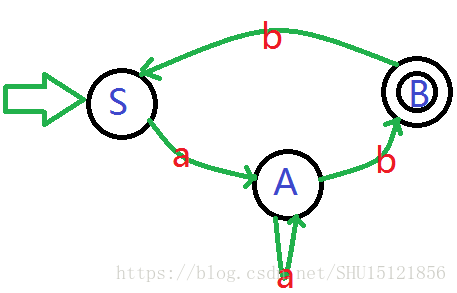
不确定的有穷自动机(NFA)

不确定的有穷自动机可以表示成一个五元组：
$$M=(K,\Sigma ,f,S,Z)即(状态集,字母表,映射,开始状态集,终止集合)$$
相比DFA，这里的映射f不再是一个单值函数，即在一个状态上给出一个输入符号可以达到多种下一状态，即"下一状态"也是一个集合，即这个映射将映射到状态集K的全体子集构成的集合，而不再是状态集本身。因此只要把上面那张图加一条状态转移线，它就不再是DFA而是NFA了：

另外，NFA的开始状态也可以有多个，所以五元组中的S现在表示了一个非空的开始状态集。

有穷自动机识别正规集

DFA是一种特殊的NFA，这里就用NFA来指代FA。要识别一个字符串是否是给定的正规集内的，也就是去识别这个字符串能否由给定的正规式产生，即按照串的顺序在NFA上走，能够从某一开始状态走到某一终止状态即表示能被该NFA识别，即该串是属于这个正规集的。

特别地，对于空串ε，只要NFA中存在即作开始状态又作终止状态的状态，或存在某一开始状态到终止状态的无条件转移(ε转移)，那么空串也可以被这个NFA接受。