没有你看不懂的Kmeans聚类算法

1 引例

经过前面一些列的介绍，我们已经接触到了多种回归和分类算法。并且这些算法有一个共同的特点，那就是它们都是有监督的（supervised）学习任务。接下来，笔者就开始向大家介绍一种无监督的（unsupervised） 经典机器学习算法——聚类。同时，由于笔者仅仅只是对Kmeans框架下的聚类算法较为熟悉，因此在后续的几篇文章中笔者将只会介绍Kmeans框架下的聚类算法，包括：Kmeans、Kmeans++和WKmeans。

在正式介绍聚类之前我们先从感性上认识一下什么是聚类。聚类的核心思想就是将具有相似特征的事物给“聚”在一起，也就是说“聚”是一个动词。俗话说人以群分，物以类聚说得就是这个道理。

如图所示为三种类型的数据样本，其中每种颜色都表示一个类别。而聚类算法的目的就是就是将各个类别的样本点分开，也就是将同一种类别的样本点聚在一起。 此时可能有人会问：这不是和分类模型一样吗？刚刚接触聚类的同学难免都会面临这么一个疑问，即聚类和分类的区别在哪儿。一句话，分类能干的事儿，聚类也能干；而聚类能干的事，分类却干不了。什么意思呢？聚类的核心思想是将具有相似特征的事物给聚在一起，也就是说聚类算法最终只能告诉我们哪些样本属于同一个类别，而不能告诉我们每个样本具体属于什么类别。因此，聚类算法在训练过程中并不需要每个样本所对应的真实标签，而分类算法却不行。

假如我们有100个样本的病例数据（包含正样本和负样本），并且通过聚类算法后我们可以将原始数据划分成两个堆，其中一个堆里面有40个样本且均为一个类别，而剩下的一个堆里面有60个样本且也为同一个类别。但具体这两个堆哪一个代表正样例，哪一个代表负样例，这是聚类算法无法告诉我们的。同时，在聚类算法中这个堆就被称之为聚类后所得到的簇（cluster）。

到此，我相信大家已经明白了聚类算法的核心思想，那聚类算法是如何完成这么一个过程的呢？

2 Kmeans聚类

在上面我们说到聚类的思想是将具有同种特征的样本聚在一起，换句话说同一个簇中的样本之间都具有一定程度的相似性，而不同簇中的样本点具有较低的相似性。因此，对于聚类算法的本质又可以看成是不同样本间相似性的一个比较，聚类的目的就是将相似度较高的样本点放到一个簇中。

由于不同类型的聚类算法有着不同的聚类原理，以及相似性评判标准。下面我们就开始介绍聚类算法中最常用的$Kmeans$聚类算法。

2.1 Kmeans算法原理

$Kmeans$聚类算法也被称为$K$均值聚类，其主要原理为：

①首先随机选择$K$个样本点作为$K$个簇的初始簇中心；

②然后计算每个样本点与这个$K$个簇中心的相似度大小，并将该样本点划分到与之相似度最大的簇中心所对应的簇中；

③根据现有的簇中样本，重新计算每个簇的簇中心；

④循环迭代步骤②③，直到目标函数收敛，即簇中心不再发生变化。

如图所示为一个聚类过程中的示例，左上角为正确标签下的样本可视化结果（每种颜色表示一个类别），其中三个黑色圆点为随机初始化的三个簇中心；当iter=1时表算法第一次迭代后的结果，可以看到此时的算法将左边的两个簇都划分到了一个簇中，而右下角的一个簇被分成了两个簇；然后依次进行反复迭代，当第四次迭代完成后，可以发现三个簇中心基本上已经位于三个簇中了，被错分的样本也在逐渐减少；当进行完第五次迭代后，可以发现基本上已经完成了对整个样本的聚类处理，只需要再迭代几次即可收敛。

以上就是$Kmeans$聚类算法在整个聚类过程中的变化情况，至于其具体的求解计算过程我们放到第二个阶段再进行介绍。

2.2 $k$值选取

经过上面的介绍，我们已经知道了$Kmeans$聚类算法的基本原理。但现在有个问题就是，我们怎么来确定聚类的$k$值呢？也就是说我们需要将数据集聚成多少个簇？如果已经很明确数据集中存在多少个簇，那么就直接指定$k$值即可；如果并不知道数据集中有多少个簇，则需要结合另外一些办法来进行选取，例如看轮廓系数、结果的稳定性等等。下面，我们通过sklearn来完成对$Kmeans$聚类算法的建模任务。

2.3 Sklearn建模

在sklearn中，我们可以通过语句from sklearn.cluster import KMeans来完成对$Kmeans$模型的导入。然后我们仍旧可以通过前面介绍三步走策略完成整个聚类任务。

def train(x, y, K):
    model = KMeans(n_clusters=K)
    model.fit(x)
    y_pred = model.predict(x)
    nmi = normalized_mutual_info_score(y, y_pred)
    print("NMI: ", nmi)

if __name__ == '__main__':
    x, y = load_data()
    train(x, y, K=3)

# 结果：
NMI:  0.7581756800057784

以上便是用sklearn搭建一个聚类模型的全部代码，可以看到其实非常简单。其中NMI为一种聚类结果评估指标，其范围为0到1，越大表示结果越好。具体的评估指标我们会在后面的文章中进行介绍。

3 Kmeans求解

现在，我们已经对$Kmeans$聚类算法的过程有了一个大致的了解，但是我们应该如何从数学的角度来对其进行描述呢？正如我们在介绍线性回归时一样，我们应该如何找到一个目标函数来对聚类结果的好坏进行刻画呢？

在上面我们说到，聚类的本质可以看成是不同样本间相似度比较的一个过程，把相似度较高的样本放到一个簇，而把相似度较低的样本点放到不同的簇中。那既然如此，我们应该怎么来衡量样本间的相似度呢？一种最常见的做法当然是计算两个样本间的欧式距离，当两个样本点离得越近就代表着两者间的相似度越高，并且这也是$Kmeans$聚类算法中的衡量标准。

因此，根据这样的准则，我们就可以将$Kmeans$聚类算法的目标函数定义为所有样本点到其对应簇中心距离的总和来刻画聚类结果的好坏程度。

3.1 Kmeans目标函数

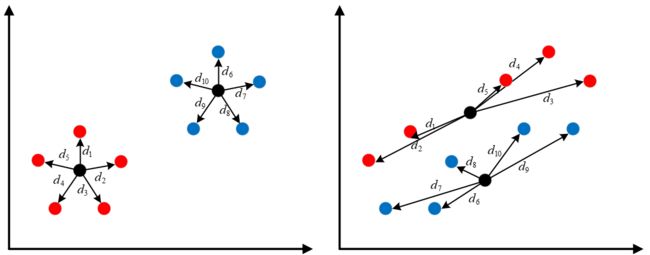
如图左右所示为同一数据集的两种不同聚类结果，其中同种颜色表示聚类后被划分到了同一个簇中，黑色圆点为聚类后的簇中心。从可视化结果来看，左图的聚类结果跟定好于右图的聚类结果。也就是说，我们可以通过最小化目标函数$d=d_1+d_2,+\cdots ,+d_{10}$来得到最优解。

设$X=\{X_1,X_2,.\cdots ,X_n\}$为一个含有$n$个样本的数据集，其中第$i$个数据对象表示为$X_i=\{x_{i1},x_{i2},\cdots ,x_{im}\}$，$m$为数据对象特征的数目。数据对象分配矩阵$U$是一个$n\times k$的0-1矩阵（里面只有0和1）,$u_{ip}$表示第$i$个样本被分到第$p$个簇中。$Z=Z_1,Z_2,\cdots ,Z_k$为$k$个簇中心向量，其中$Z_p=\{z_{p1},z_{p2},\cdots ,z_{pm}\}$为第$p$个簇中心。则$Kmeans$聚类算法的目标函数可以写为：
$$P(U,Z)=\sum _{p=1}^k\sum _{i=1}^n{u}_{ip}\sum _{j=1}^m(x_{ij}-z_{pj}{)}^2\text{\hspace{1em}(1)}$$
并且服从于约束条件：
$$\sum _{p=1}^k{u}_{ip}=1\text{\hspace{1em}(2)}$$
式子$(1)$看起来稍微有点复杂，但是其表示的意思就是累加各个样本点到其对应簇中心的距离和。由于一个数据集有多个簇，每个簇中有多个样本，每个样本又有多个维度，因此式子$(1)$中就存在了三个求和符号。其次，以上图为例再来简单说一下分配矩阵$U$。由上图（左）可知，数据集中一共有两个簇，且假设前5个样本为一个簇，后5个样本为一个簇，则分配矩阵为：
$$U_{[10,2]}=\left[\begin{array}{cc}1& 0\\ 1& 0\\ 1& 0\\ 1& 0\\ 1& 0\\ 0& 1\\ 0& 1\\ 0& 1\\ 0& 1\\ 0& 1\end{array}\right]$$

3.2 最小化目标函数

到目前为止，我们就得到了$Kmeans$聚类算法的目标函数，接下来只需要对其进行最小化就能得到对应未知变量$U,Z$的更新公式。由于文章篇幅有限，具体的求解过程和编码实现将放在下一篇文章中进行介绍。

4 总结

在这篇文章中，笔者首先介绍了聚类算法的基本思想；然后以$Kmeans$聚类算法为例，介绍了其聚类过程并进行了可视化；接着介绍了如何通过sklearn来完成对于$Kmeans$聚类模型的搭建；最后介绍了$Kmeans$聚类算法的目标函数。本次内容就到此结束，感谢阅读！

若有任何疑问与见解，请发邮件至[email protected]并附上文章链接，青山不改，绿水长流，月来客栈见！

引用

[1] 示例代码 ： https://github.com/moon-hotel/MachineLearningWithMe

近期文章

[1]原来这就是支持向量机

[2]这就是决策树的思想

[3]朴素贝叶斯算法

[4]K最近邻算法