时间序列数据(Time Series Data)是按时间排序的数据,利率、汇率和股价等都是时间序列数据。时间序列数据的时间间隔可以是分和秒(如高频金融数据),也可以是日、周、月、季度、年以及甚至更大的时间单位。数据分析解决方案提供商 New Relic 在其博客上介绍了为时间序列数据优化 K-均值聚类速度的方法。机器之心对本文进行了编译介绍。
在 New Relic,我们每分钟都会收集到 13.7 亿个数据点。我们为我们的客户收集、分析和展示的很大一部分数据都是时间序列数据。为了创建应用与其它实体(比如服务器和容器)之间的关系,以便打造 New Relic Radar 这样的新型智能产品,我们正在不断探索更快更有效的对时间序列数据分组的方法。鉴于我们所收集的数据的量是如此巨大,更快的聚类时间至关重要。
加速 k-均值聚类
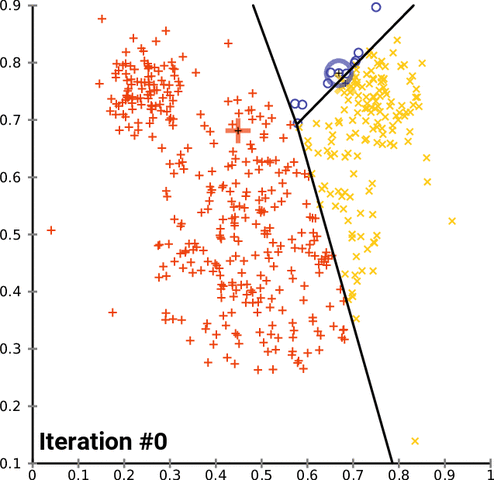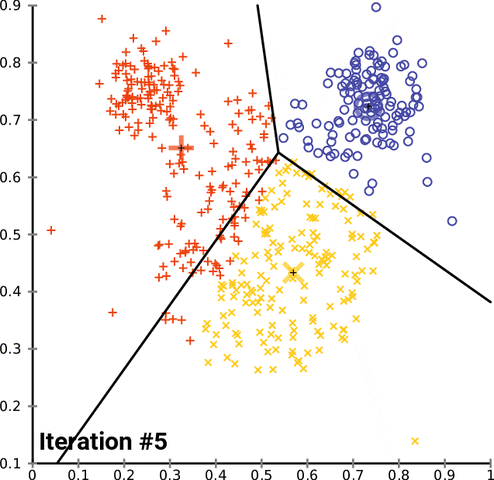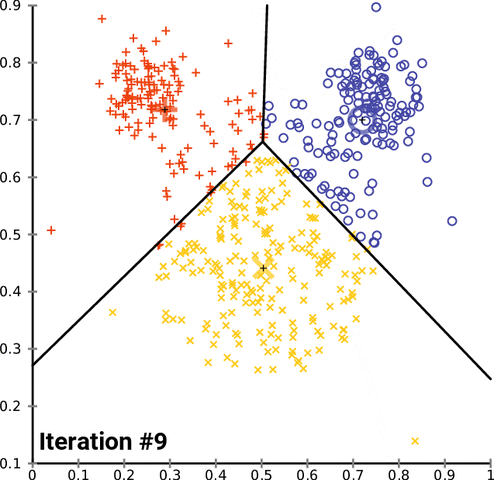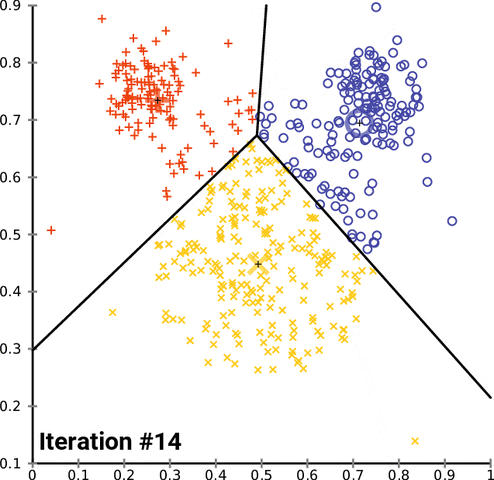
k-均值聚类是一种流行的分组数据的方法。k-均值方法的基本原理涉及到确定每个数据点之间的距离并将它们分组成有意义的聚类。我们通常使用平面上的二维数据来演示这个过程。以超过二维的方式聚类当然是可行的,但可视化这种数据的过程会变得更为复杂。比如,下图给出了 k-均值聚类在两个任意维度上经过几次迭代的收敛情况:
不幸的是,这种方法并不能很好地用于时间序列数据,因为它们通常是随时间变化的一维数据。但是,我们仍然可以使用一些不同的函数来计算两个时间序列数据之间的距离因子(distance factor)。在这些案例中,我们可以使用均方误差(MSE)来探索不同的 k-均值实现。在测试这些实现的过程中,我们注意到很多实现的表现水平都有严重的问题,但我们仍然可以演示加速 k-均值聚类的可能方法,在某些案例中甚至能实现一个数量级的速度提升。
这里我们将使用 Python 的 NumPy 软件包。如果你决定上手跟着练习,你可以直接将这些代码复制和粘贴到 Jupyter Notebook 中。让我们从导入软件包开始吧,这是我们一直要用到的东西:
-
import time -
import numpy as np -
import matplotlib.pyplot as plt -
-
%matplotlib inline
在接下来的测试中,我们首先生成 10000 个随机时间序列数据,每个数据的样本长度为 500。然后我们向随机长度的正弦波添加噪声。尽管这一类数据对 k-均值聚类方法而言并不理想,但它足以完成未优化的实现。
-
n = 10000 -
ts_len = 500 -
-
phases = np.array(np.random.randint(0, 50, [n, 2])) -
pure = np.sin([np.linspace(-np.pi * x[0], -np.pi * x[1], ts_len) for x in phases]) -
noise = np.array([np.random.normal(0, 1, ts_len) for x in range(n)]) -
-
signals = pure * noise -
-
# Normalize everything between 0 and 1 -
signals += np.abs(np.min(signals)) -
signals /= np.max(signals) -
-
plt.plot(signals[0])
第一个实现
让我们从最基本和最直接的实现开始吧。euclid_dist 可以为距离函数实现一个简单的 MSE 估计器,k_means 可以实现基本的 k-均值算法。我们从我们的初始数据集中选择了 num_clust 随机时间序列数据作为质心(代表每个聚类的中心)。在 num_iter 次迭代的过程中,我们会持续不断地移动质心,同时最小化这些质心与其它时间序列数据之间的距离。
-
def euclid_dist(t1, t2): -
return np.sqrt(((t1-t2)**2).sum()) -
def k_means(data, num_clust, num_iter): -
centroids = signals[np.random.randint(0, signals.shape[0], num_clust)] -
-
for n in range(num_iter): -
assignments={} -
for ind, i in enumerate(data): -
min_dist = float('inf') -
closest_clust = None -
for c_ind, j in enumerate(centroids): -
dist = euclid_dist(i, j) -
if dist < min_dist: -
min_dist = dist -
closest_clust = c_ind -
-
if closest_clust in assignments: -
assignments[closest_clust].append(ind) -
else: -
assignments[closest_clust]=[] -
assignments[closest_clust].append(ind) -
-
for key in assignments: -
clust_sum = 0 -
for k in assignments[key]: -
clust_sum = clust_sum + data[k] -
centroids[key] = [m / len(assignments[key]) for m in clust_sum] -
-
return centroids
-
t1 = time.time() -
centroids = k_means(signals, 100, 100) -
t2 = time.time() -
print("Took {} seconds".format(t2 - t1))
-
Took 1138.8745470046997 seconds
聚类这些数据用去了接近 20 分钟。这不是很糟糕,但肯定算不上好。为了在下一个实现中达到更快的速度,我们决定去掉尽可能多的 for 循环。
向量化的实现
使用 NumPy 的一大优势是向量化运算。(如果你不太了解向量化运算,请参考这个链接:http://www.scipy-lectures.org/intro/numpy/operations.html)
k-均值算法要求每个质心和数据点都成对地进行比较。这意味着在我们之前的迭代中,我们要将 100 个质心和 10000 个时间序列数据分别进行比较,也就是每次迭代都要进行 100 万次比较。请记住每次比较都涉及到两个包含 500 个样本的集合。因为我们迭代了 100 次,那就是说我们总共比较了 1 亿次——对于单个 CPU 而言算是相当大的工作量了。尽管 Python 是一种还算高效的语言,但效率还赶不上用 C 语言写的指令。正是由于这个原因,NumPy 的大部分核心运算都是用 C 语言写的,并且还进行了向量化以最小化由循环带来的计算开销。
我们来探索一下我们可以如何向量化我们的代码,从而去掉尽可能多的循环。
首先,我们将代码分成不同的功能模块。这能让我们更好地理解每个部分所负责的工作。接下来,我们修改 calc_centroids 步骤以便仅在质心上迭代(而不是在每个时间序列数据上)。这样,我们将所有时间序列数据和一个质心传递给 euclid_dist。我们还可以预先分配 dist 矩阵,而不是将其当成一个词典进行处理并随时间扩展它。NumPy 的 argmin 可以一次性比较每个向量对。
在 move_centroids 中,我们使用向量运算去掉了另一个 for 循环,而且我们只在独特的质心集上迭代。如果我们丢失了一个质心,我们就通过从我们的时间序列数据集中进行随机选择来加入合适的数字(这在实际应用的实践中很罕见)。
最后,我们添加一个提前停止(early stopping)来检查 k_means——如果质心不再更新,就停止迭代。
来看看代码:
-
def euclid_dist(t1, t2): -
return np.sqrt(((t1-t2)**2).sum(axis = 1)) -
-
def calc_centroids(data, centroids): -
dist = np.zeros([data.shape[0], centroids.shape[0]]) -
-
for idx, centroid in enumerate(centroids): -
dist[:, idx] = euclid_dist(centroid, data) -
-
return np.array(dist) -
-
def closest_centroids(data, centroids): -
dist = calc_centroids(data, centroids) -
return np.argmin(dist, axis = 1) -
-
def move_centroids(data, closest, centroids): -
k = centroids.shape[0] -
new_centroids = np.array([data[closest == c].mean(axis = 0) for c in np.unique(closest)]) -
-
if k - new_centroids.shape[0] > 0: -
print("adding {} centroid(s)".format(k - new_centroids.shape[0])) -
additional_centroids = data[np.random.randint(0, data.shape[0], k - new_centroids.shape[0])] -
new_centroids = np.append(new_centroids, additional_centroids, axis = 0) -
-
return new_centroids -
-
def k_means(data, num_clust, num_iter): -
centroids = signals[np.random.randint(0, signals.shape[0], num_clust)] -
last_centroids = centroids -
-
for n in range(num_iter): -
closest = closest_centroids(data, centroids) -
centroids = move_centroids(data, closest, centroids) -
if not np.any(last_centroids != centroids): -
print("early finish!") -
break -
last_centroids = centroids -
-
return centroids
-
t1 = time.time() -
centroids = k_means(signals, 100, 100) -
t2 = time.time() -
print("Took {} seconds".format(t2 - t1))
-
adding 1 centroid(s) -
early finish! -
took 206.72993397712708 seconds
耗时 3.5 分钟多一点。很不错!但我们还想完成得更快。
k-means++ 实现
我们的下一个实现使用了 k-means++ 算法。这个算法的目的是选择更优的初始质心。让我们看看这种优化方法有没有用……
-
def init_centroids(data, num_clust): -
centroids = np.zeros([num_clust, data.shape[1]]) -
centroids[0,:] = data[np.random.randint(0, data.shape[0], 1)] -
-
for i in range(1, num_clust): -
D2 = np.min([np.linalg.norm(data - c, axis = 1)**2 for c in centroids[0:i, :]], axis = 0) -
probs = D2/D2.sum() -
cumprobs = probs.cumsum() -
ind = np.where(cumprobs >= np.random.random())[0][0] -
centroids[i, :] = np.expand_dims(data[ind], axis = 0) -
-
return centroids -
-
def k_means(data, num_clust, num_iter): -
centroids = init_centroids(data, num_clust) -
last_centroids = centroids -
-
for n in range(num_iter): -
closest = closest_centroids(data, centroids) -
centroids = move_centroids(data, closest, centroids) -
if not np.any(last_centroids != centroids): -
print("Early finish!") -
break -
last_centroids = centroids -
-
return centroids
-
t1 = time.time() -
centroids = k_means(signals, 100, 100) -
t2 = time.time() -
print("Took {} seconds".format(t2 - t1))
-
early finish! -
took 180.91435194015503 seconds
相比于我们之前的迭代,加入 k-means++ 算法能得到稍微好一点的性能。但是,当我们将其并行化之后,这种优化方法才真正开始带来显著回报。
并行实现
到目前为止,我们所有的实现都是单线程的,所以我们决定探索 k-means++ 算法的并行化部分。因为我们在使用 Jupyter Notebook,所以我们选择使用用于并行计算的 ipyparallel 来管理并行性(ipyparallel 地址:https://github.com/ipython/ipyparallel)。使用 ipyparallel,我们不必担心整个服务器分叉,但我们需要解决一些特殊问题。比如说,我们必须指示我们的工作器节点加载 NumPy。
-
import ipyparallel as ipp -
c = ipp.Client() -
v = c[:] -
v.use_cloudpickle() -
-
with v.sync_imports(): -
import numpy as np
关于加载工作器更多详情,请参阅 ipyparallel 上手指南:https://ipyparallel.readthedocs.io/en/latest/
在这一个实现中,我们的重点放在并行化的两个方面。首先,calc_centroids 有一个在每个质心上迭代并将其与我们的时间序列数据进行比较的循环。我们使用了 map_sync 来将这些迭代中的每一个发送到我们的工作器。
接下来,我们并行化 k-means++ 质心搜索中一个相似的循环。注意其中对 v.push 的调用:因为我们的 lambda 引用的数据,我们需要确保它在工作器节点上是可用的。我们通过调用 ipyparallel 的 push 方法来将该变量复制到工作器的全局范围中,从而实现了这一目标。
看看代码:
-
def calc_centroids(data, centroids): -
return np.array(v.map_sync(lambda x: np.sqrt(((x - data)**2).sum(axis = 1)), centroids)) -
def closest_centroids(points, centroids): -
dist = calc_centroids(points, centroids) -
return np.argmin(dist, axis=0) -
-
def init_centroids(data, num_clust): -
v.push(dict(data=data)) -
centroids = np.zeros([num_clust, data.shape[1]]) -
centroids[0,:] = data[np.random.randint(0, data.shape[0], 1)] -
for i in range(1, num_clust): -
D2 = np.min(v.map_sync(lambda c: np.linalg.norm(data - c, axis = 1)**2, centroids[0:i,:]), axis = 0) -
probs = D2/D2.sum() -
cumprobs = probs.cumsum() -
ind = np.where(cumprobs >= np.random.random())[0][0] -
centroids[i, :] = np.expand_dims(data[ind], axis = 0) -
-
return centroids
-
t1 = time.time() -
centroids = k_means(signals, 100, 100) -
t2 = time.time() -
print("Took {} seconds".format(t2 - t1))
-
adding 2 centroid(s) -
early finish! -
took 143.49819207191467 seconds
结果只有两分钟多一点,这是我们目前实现的最快速度!
接下来:更快!
在这些测试中,我们都只使用了中央处理器(CPU)。CPU 能提供方便的并行化,但我们认为再多花点功夫,我们就可以使用图形处理器(GPU)来实现聚类,且速度将得到一个数量级的提升。我们也许可以使用 TensorFlow 来实现,这是一个用于数值计算和机器学习的开源软件。实际上,TensorFlow 已经包含了 k-均值实现,但我们基本上肯定还是需要对其进行调整才能将其用于时间序列聚类。不管怎样,我们都不会停下寻找更快更高效的聚类算法的步伐,以帮助管理我们的用户的数据。