机器学习 -- 信用卡评分模型 -- 互联网金融风控

互联网金融主要分为资金类和资产类。资金类主要是理财产品，吸储，主要指标是用户转化、留存和复投，重在客户运营。资产类主要是贷款，包括消费金融和现金贷，小额贷款属于此类，主要目的是用户转化，还款和风险控制，信用卡评分模型就属于风险控制。

信用评分作用是对贷款申请人（信用卡申请人）做风险评估分值的方法。 信用卡评分是以大量数据的统计结果为基础，根据客户提供的资料和历史数据对客户的信用进行评估，评分卡模型一般分为三类：A卡：申请评分卡，B卡：行为评分卡，C卡：催收评分卡。
本文主要涉及的为申请评分卡，申请评分卡的目标主要是区分好客户和坏客户，评分卡的结果为高分数的申请人意味着比低分数的申请人的风险低。
本文主要参考以下两篇文章，并对部分步骤进行了简化，本次最大的改进在于引入映射和矩阵计算，提高了效率：
文章1：https://blog.csdn.net/weixin_34021089/article/details/93744181?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
文章2：https://blog.csdn.net/baidu_38409988/article/details/100127904?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
建模的主要步骤为：
数据读取 ==》数据预处理 ==》探索性分析 ==》特征选择 ==》模型搭建 ==》模型评估 ==》分数计算

一、数据读取

import pandas as pd
import numpy as np

data = pd.read_csv('cs-training.csv',encoding='utf-8')
data.head()

二、数据预处理

data = data.drop_duplicates()
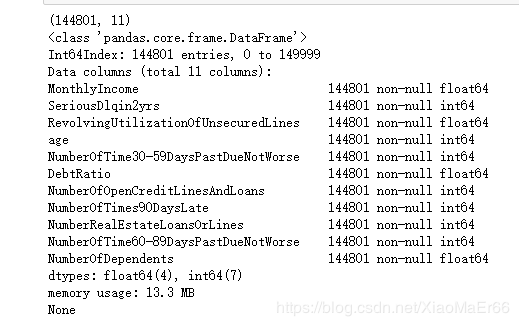
data.info()

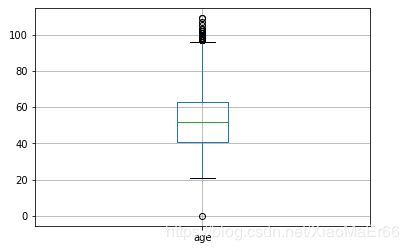
#2.1 画箱线图 看异常情况
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False

data.boxplot(column=['age'])
plt.show()

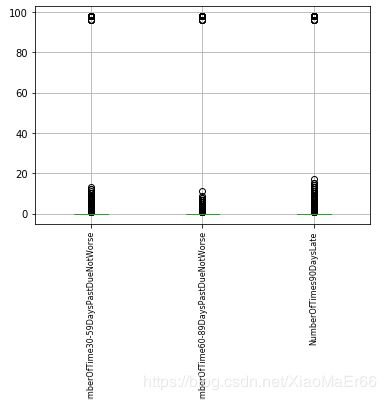
cols =['NumberOfTime30-59DaysPastDueNotWorse','NumberOfTime60-89DaysPastDueNotWorse','NumberOfTimes90DaysLate']
data.boxplot(column=cols)
plt.xticks(rotation=90,fontsize=8)
plt.show()

在这里插入图片描述

##2.2删除年龄大于90小于等于0的
data = data[(data['age']>0)&(data['age']<90)]

#2.3 删除逾期贷款异常值
data = data[data['NumberOfTime30-59DaysPastDueNotWorse']<90]

#3.1 删除NumberOfTime30-59DaysPastDueNotWorse空值
data = data.drop(data[data['NumberOfDependents'].isnull()].index)

#3.2MonthlyIncome 随机森林建模补空
#调整列的位置，将MonthlyIncome放在最前面
data = data[['MonthlyIncome','SeriousDlqin2yrs', 'RevolvingUtilizationOfUnsecuredLines', 'age',
       'NumberOfTime30-59DaysPastDueNotWorse', 'DebtRatio',
       'NumberOfOpenCreditLinesAndLoans', 'NumberOfTimes90DaysLate',
       'NumberRealEstateLoansOrLines', 'NumberOfTime60-89DaysPastDueNotWorse',
       'NumberOfDependents']]
#建模，选择最优参数并补充空值
from sklearn.ensemble import RandomForestRegressor
from sklearn.cross_validation import train_test_split,cross_val_score
from sklearn.model_selection import GridSearchCV

train = data[data['MonthlyIncome'].notnull()]
x_train,x_test,y_train,y_test= train_test_split(train.iloc[:,1:],train.iloc[:,0],test_size=0.25,random_state=22)
test = data[data['MonthlyIncome'].isnull()]
x_pre = test.iloc[:,1:]

def params_fit(x_train,y_train):
    s_list =[]
    i_list =[]
    for i in range(100,200,10):
        rf = RandomForestRegressor(n_estimators=i,random_state=42)
        scores = cross_val_score(rf,x_train,y_train,cv=3).mean()
        s_list.append(scores)
        i_list.append(i)
    max_scores =max(s_list)
    max_es = s_list.index(max_scores)*10+100
    paras = {'max_depth':np.arrange(3,10,1)}
    rfs = RandomForestRegressor(n_estimators=max_es,random_state=42)
    gs = GridSearchCV(rfs,param_grid=paras,cv=3)
    fun = gs.fit(x_train,y_train)
    sc = fun.best_score_
    para = fun.best_params_
    result = rf.predict(x_test)
    return max_es,para['max_depth']
    
max_es,para['max_depth'] = params_fit(x_train,y_train)

def set_missing(x_train,y_train,x_pre,data):
    rf =  RandomForestRegressor(n_estimators=150,max_depth=3,random_state=42)
    rf.fit(x_train,y_train)
    y_pre = rf.predict(x_pre)
    data.loc[data['MonthlyIncome'].isnull(),'MonthlyIncome'] = y_pre
    return data

data = set_missing(x_train,y_train,x_pre,data)

三、探索性分析

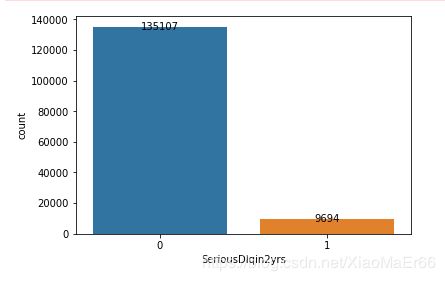
#查看整体好坏个数
import seaborn as sns
s_count = data['SeriousDlqin2yrs'].value_counts()
sns.countplot(data['SeriousDlqin2yrs'])
for a,b in enumerate(s_count):
    plt.text(a,b+0.2,b,ha='center',va='center')
plt.show()

#好坏客户0,1转换，好1，坏0
data['SeriousDlqin2yrs'] = 1-data['SeriousDlqin2yrs']
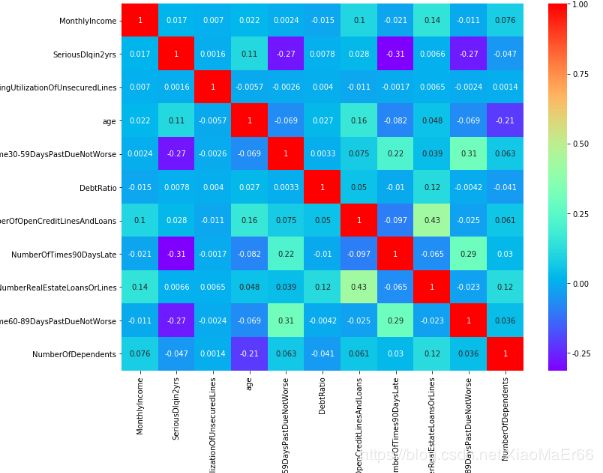
#相关性分析
plt.figure(figsize=(12,9))
sns.heatmap(data.corr(),annot=True,cmap='rainbow')
plt.xticks(rotation=90)
plt.show()

四、数据特征选择
根据特征对结果的影响选择影响较大的进行分析，主要看特征的IV（数据价值）IV<0.02时，对结果影响较小，不具有参考性。

IV，WOE的具体解释及计算过程可参考下文，解释的比较详细，容易理解：https://blog.csdn.net/kevin7658/article/details/50780391

变量分箱 将连续变量离散化，特征离散化后，模型会更稳定，降低了模型过拟合的风险。同时由于逻辑回归模型的每个变量的每种情况都会有对应的特征权值，使用分箱之后可以降低数据量，使模型泛化能力增强。
针对连续型变量，如年龄、资产负债率，在一个连续变化的区间，采用最优分箱。分别对特征进行分段，计算WOE值。

data = data[[ 'SeriousDlqin2yrs','MonthlyIncome',
       'RevolvingUtilizationOfUnsecuredLines', 'age',
       'NumberOfTime30-59DaysPastDueNotWorse', 'DebtRatio',
       'NumberOfOpenCreditLinesAndLoans', 'NumberOfTimes90DaysLate',
       'NumberRealEstateLoansOrLines', 'NumberOfTime60-89DaysPastDueNotWorse',
       'NumberOfDependents']]
#1.1对连续值进行最优分段,不连续的值自定义分段
import numpy as np
from scipy import stats

ninf = float('-inf')
pinf = float('inf')

def optical_cut(x,n):
    cut = pd.cut(x,n)
    return cut
    
#对于连续型变量，采用均分，离散型变量，自定义分段
data1 = data.copy()
data1['cut1'] = pd.qcut(data['MonthlyIncome'],20,duplicates='drop')
data1['cut2'] = pd.qcut(data['RevolvingUtilizationOfUnsecuredLines'],20,duplicates='drop')
data1['cut3']= pd.qcut(data['age'],20,duplicates='drop')
bins4 = [ninf,0,1,2,3,5,pinf]
data1['cut4'] = pd.cut(data['NumberOfTime30-59DaysPastDueNotWorse'],bins4)
data1['cut5']= pd.qcut(data['DebtRatio'],20,duplicates='drop')
bins6 = [ninf,1,2,3,5,pinf]
data1['cut6'] = pd.cut(data['NumberOfOpenCreditLinesAndLoans'],bins6)
bins7 = [ninf,0,1,2,3,5,pinf]
data1['cut7'] = pd.cut(data['NumberOfTimes90DaysLate'],bins7)
bins8 = [ninf,0,1,2,3,pinf]
data1['cut8'] = pd.cut(data['NumberRealEstateLoansOrLines'],bins8) 
bins9 = [ninf,0,1,2,3,5,pinf]
data1['cut9']= pd.cut(data['NumberOfTime60-89DaysPastDueNotWorse'],bins9)
bins10 = [ninf,0,1,2,3,5,pinf]
data1['cut10'] = pd.cut(data['NumberOfDependents'],bins10)

#woe、IV值计算
#好坏客户比例
sp1 = data1['SeriousDlqin2yrs'].sum()
sp0 = data1['SeriousDlqin2yrs'].count()-data1['SeriousDlqin2yrs'].sum()
srate =sp1/sp0

def woe_data(cut):
    sum1 = data1['SeriousDlqin2yrs'].groupby(cut,as_index=True).sum()
#     sum1 = sum1.map(lambda x: x if x != 0 else 1) #个别区间段存在好/坏个数为0的情况，计算出的woe值会出现+无穷或者—无穷的情况，最好保证分组里面至少有1个正/负类型。
    p1 = sum1/sp1
    sum0 = (data1['SeriousDlqin2yrs'].groupby(cut,as_index=True).count()-data1['SeriousDlqin2yrs'].groupby(cut,as_index=True).sum())
#     sum0 = sum0.map(lambda x: x if x != 0 else 1)
    p0 = sum0/sp0 
    woe =np.log(p1/p0)
    iv = ((p1-p0)*woe).sum()
    return woe,iv
    
woe1,iv1 = woe_data(data1['cut1'])
woe2,iv2 = woe_data(data1['cut2'])
woe3,iv3 = woe_data(data1['cut3'])
woe4,iv4 = woe_data(data1['cut4'])
woe5,iv5 = woe_data(data1['cut5'])
woe6,iv6 = woe_data(data1['cut6'])
woe7,iv7 = woe_data(data1['cut7'])
woe8,iv8 = woe_data(data1['cut8'])
woe9,iv9 = woe_data(data1['cut9'])
woe10,iv10 = woe_data(data1['cut10'])

def woe_re(i,woe):
    cut = 'cut'+str(i)
    woes = 'woe'+str(i)
    dict_temp = {'cut':woe.index,woes:woe}
    df_temp = pd.DataFrame(dict_temp)
    data1[woes] = data1.merge(df_temp,how='left',left_on=cut,right_on='cut')[woes]
    
for i,woe in enumerate([woe1,woe2,woe3,woe4,woe5,woe6,woe7,woe8,woe9,woe10]):
    i += 1
    woe_re(i,woe)
    
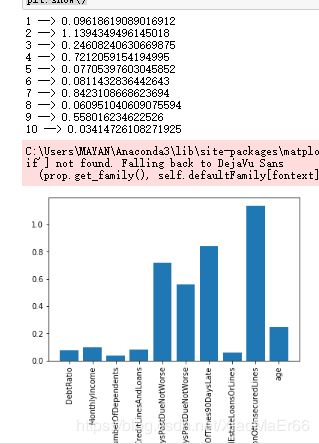
ivlist = [iv1,iv2,iv3,iv4,iv5,iv6,iv7,iv8,iv9,iv10]
for i in range(1,11):
    print(i,'-->',ivlist[i-1])
names=['MonthlyIncome',
       'RevolvingUtilizationOfUnsecuredLines', 'age',
       'NumberOfTime30-59DaysPastDueNotWorse', 'DebtRatio',
       'NumberOfOpenCreditLinesAndLoans', 'NumberOfTimes90DaysLate',
       'NumberRealEstateLoansOrLines', 'NumberOfTime60-89DaysPastDueNotWorse',
       'NumberOfDependents']
plt.bar(names,ivlist)
plt.xticks(rotation=90)
plt.show()

#根据IV值选出重要的5个特征进行建模
cols_new =[
       'RevolvingUtilizationOfUnsecuredLines', 'age',
       'NumberOfTime30-59DaysPastDueNotWorse','NumberOfTimes90DaysLate',
 'NumberOfTime60-89DaysPastDueNotWorse'
       ]
#二分类选用逻辑回归模型比较合适       
from sklearn.linear_model import LogisticRegression

X= data1[cols_new]
Y=data1['SeriousDlqin2yrs']
X_train,X_test,Y_train,Y_test = train_test_split(X,Y,test_size=0.25,
                                                 random_state=11)
lr = LogisticRegression()
clf =lr.fit(X_train,Y_train)
print(clf.score(X_test,Y_test))
Y_pre = clf.predict(X_test)
coe = clf.coef_
print(coe)

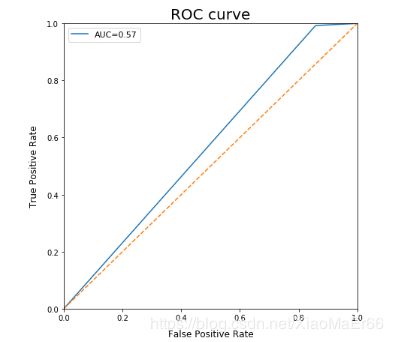
六、模型评估
ROC——AUC曲线评估，曲线越靠左越靠上，说明效果越好。本次AUC只有0.57，建模效果不好，参考文章中AUC为0.85，经过多次调试，效果依旧不好，有懂的大神欢迎指点讨论。

fpr,tpr,thresholds=roc_curve(Y_test,Y_pre)
AUC=auc(fpr,tpr)
plt.figure(figsize=(7,7))
plt.plot(fpr,tpr,label='AUC=%.2f'%AUC)
plt.plot([0,1],[0,1],'--')
plt.xlim([0,1])
plt.ylim([0,1])
plt.xlabel('False Positive Rate',fontdict={'fontsize':12},labelpad=10)
plt.ylabel('True Positive Rate',fontdict={'fontsize':12},labelpad=10)
plt.title('ROC curve',fontdict={'fontsize':20})
plt.legend(loc=0,fontsize=11)

七、分数转化
Score = offset + factor* log(odds) 在建立标准评分卡之前，需要选取几个评分卡参数：基础分值、 PDO（比率翻倍的分值）和好坏比。 这里，采用600分为基础分值，PDO为20 （每高20分好坏比翻一倍），好坏比取20。
factor 是模型系数 ，offset是偏移量 ，odds =p_good/p_bad

factor = 20/np.log(2)
offset = 600-20*np.log(20)/np.log(2)
basescore = coe[0]*factor+offset

woecols =['woe2','woe3','woe4','woe7','woe9']

df_matrix = data1[woecols].as_matrix()
coe_matrix = np.array(coe).reshape(len(coe[0]),1)
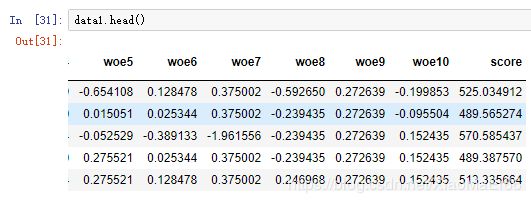
data1['score'] = np.dot(df_matrix,coe_matrix)*factor+offset

good = data1[data1['SeriousDlqin2yrs']==1]['score']
bad = data1[data1['SeriousDlqin2yrs']==0]['score']
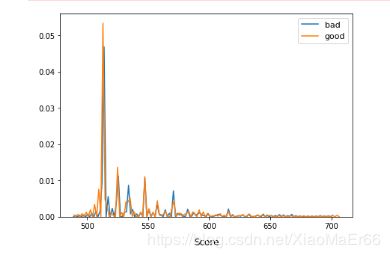
plt.figure(figsize=(7,5))
sns.distplot(bad,bins=50,hist=False,label='bad')
sns.distplot(good,bins=50,hist=False,label='good')
plt.xlabel('Score',fontdict={'fontsize':12},labelpad=10)
plt.legend(loc=0,fontsize=11)
plt.show()

总结
评分后看分数分布，分数并很好的将好坏客户明显得区分开，此次建模效果并不好，如何进一步优化，使得模型效果更好，欢迎讨论指导。

代码和原始数据如下，欢迎一起探讨：
链接：https://pan.baidu.com/s/1wz_T-ox4YqpZuNQ0dhIk3Q
提取码：167s

更新
复盘过程中，发现样本分布不均匀，偏差较大，使用过采样的方法，重新生成样本，进行重新训练和评估，准确率有所下降至83%，但AUC上升至0.75，总体来说效果比之前好很多。
在建模前，对样本进行了生成，并进行了参数调优。

from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV

X= data1[cols_new]
Y=data1['SeriousDlqin2yrs']
x_train,X_test,y_train,Y_test = train_test_split(X,Y,test_size=0.25,
                                                 random_state=11)
#样本不均衡，下采样生成样本
from imblearn.over_sampling import SMOTE

oversample = SMOTE(random_state= 0)
X_train,Y_train = oversample.fit_sample(x_train,y_train)

lr = LogisticRegression()
params = {'C':[0.001,0.01,0.1,1,10],'penalty':['l1','l2']}
gr = GridSearchCV(lr,param_grid=params,cv=5)
gr.fit(X_train,Y_train)
print(gr.score(X_test,Y_test),gr.best_params_)

从ROC_AUC曲线可以看出，模型泛化性能及稳定性能有答复提升。