【数据分析】数据预处理中的数据变换
目录
数据变换
二值化(Binarization)
离散化(Discretization)(特征分箱)
哑编码(Dummy coding)
标准化(Standardization)
规范化(Normalization)
数据变换
- 二值化(用于区分的属性)
- 连续特征离散化(特征分箱)
- 等宽法(max-min)/x组
- 等分法 (样本数)/x组
- 多变量:聚类
- 哑变量(对于定类变量)
- 标准化
- 规范化
- 属性构造(衍生变量)
- 函数变换(可用在处理异常值)
- 小波变换
二值化(Binarization)
二值化,顾名思义就是将一个字段转换为仅有两个可能值。二值化通过设定一个阈值,原字段大于阈值的被设定为1,否则为0,即转换函数为指示函数:
对于示例数据集当中的"IMEI"字段是手机串码(原本为15位),一部移动设备对应一个,是全球唯一的,这样的字段与ID字段一样无法进入模型。通过观察,发现有大量的记录IMEI为空值(现已填补为0),因此可以将有IMEI的设置为1,没有的设置为0。在scikit-learn的preprocessing中,使用Binarizer可以将字段二值化,示例如下:
除了使用Binarizer,在可以使用pandas.cut对数据进行离散化,这种方式通过传入一个用于表示阈值的"bins"参数,将数据进行分割,如下所示:
需要注意的是传入的阈值列表是包含了上下界的,切割的区间为左开右闭,即切割后的两个区间为(-∞,0]和(0,+∞)。如果要切割成多个区域,只需把所有阈值以列表形式传入"bins"参数即可。
离散化(Discretization)(特征分箱)
连续型特征经常成为模型不稳定的来源,此外,连续型特征可能与目标变量呈现复杂的相关性,而将连续型特征根据一定方法转化为离散特征后可能带来模型效果的提升。
常用的离散化方法
- 等宽离散
- 等分离散
- 人工离散等
- 二值化(Binarization)可以看做是离散化的特殊情况
离散化的基本原理是将连续数据划分至不同的区间(也称为“分箱”),使用区间的编码来代替原始数据即可。例如:等宽离散的区间是按照数据的极差进行平均划分的,其每个区间的宽度相等;等分离散化是按照数据的分位数划分的,其每个区间内的样本量相等(或接近相等);人工离散化则是根据业务理解进行区间划分的。一个针对年龄进行不同离散化的例子如下图所示:
为了演示离散化,我们将示例数据集中的“入网时间”转化为“在网时长”:
至此,我们“在网时长”属于连续型特征,我们可以对其进行离散化。
1. 等宽离散
使用Pandas进行等宽离散的例子如下:
离散化后,可以看到(1.892, 36.913] 区间内的样本量最多,(141.453, 176.3]区间内样本量最少,在不同的区间内用户离网率(mean字段)呈现有规律的变化。这里可以注意一下,pandas等宽离散的每个区间都是左开右闭的。
pandas提供的cut方法可以通过传输label参数,将每个离散化后的区间用指定的编码进行表示,并且新生成的编码是有序的。例如使用0到4的整数来表示等宽离散的每个区间如下:
可见,原始的在网时长字段可以被用0到4来替代,函数同时返回了划分区间的每个阈值。
2. 等分离散
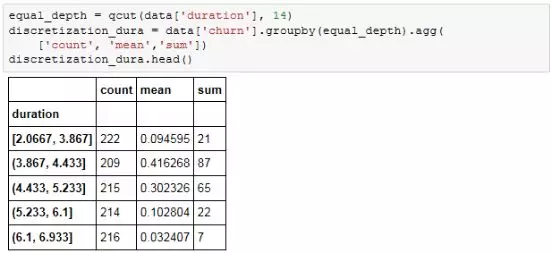
pandas提供的qcut方法可用于进行等分离散,但有bug,所以这里重新定义一个qcut函数:
该函数使用分位数确定某一列特征的划分区间,再使用pandas.cut将数据按照划分区间进行离散,这里的pandas.cut函数因为指定了区间,将不再按照默认的等宽方式离散了。
使用自定义的函数可以方便地对数据进行等分离散:
可以看到,离散化后每个区间内的样本量基本相等,各区间内的用户离网率呈现出一定的规律。也正是因为每个区间的样本量基本相等,这个离网率显得更有可信度。如果采用其他离散化方法,可能造成某些区间的样本量过少,该区间的离网率自然很难有说服力。本例中我们将离网率按等分离散的区间绘制柱状图如下:
3. 人工离散
仅需要人工指定区间划分的阈值就可以很容易地使用pandas.cut进行人工离散化,如下例:
本例中,为了保证能将所有数据都包含进来,分别使用正负无穷大作为最大与最小值。
哑编码(Dummy coding)
对于无序的分类变量,许多模型不支持其运算(在R中许多模型,例如回归模型,会自动将因子变量转换为哑变量,省去了很多麻烦),可以先生成哑变量,再进行深入分析。哑变量被认为是量化了的分类变量,因此应用非常广泛。
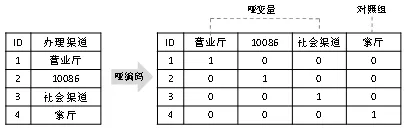
哑变量又称虚拟变量或虚设变量,一般使用0和1来表示分类变量的值是否处于某一分类水平,例如账户ID1~4的办理渠道如图18-1左图所示,进行哑编码后用0和1来表示各记录是的具体取值情况,如图18-1右图所示:
图18-1
一般有m个分类水平的变量经过哑编码之后,会生成m个哑变量,各个哑变量之间两两互斥,应用中一般仅保留其中m-1个进入模型,留下1个作为对照组,对照组可以通过其他m-1个哑变量完全还原出来。在使用哑变量建模时,一般需要保证由这m-1个哑变量都能进入模型,或者都不进入模型。
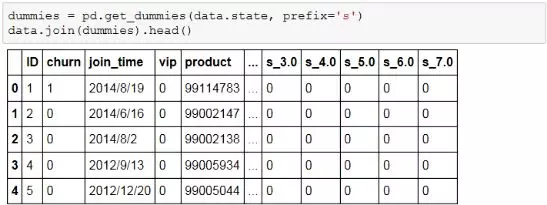
在pandas中可以使用get_dummies函数来对分类变量进行哑编码,新生成的哑变量与原变量的分类水平数相等,对照组可自行选择,get_dummies使用方法如下所示:
另外,scikit-learn的preprocessing当中,可以使用OneHotEncoder对数据进行哑编码,同样会生成与原变量水平数相等的哑变量,代码如下:
标准化(Standardization)
在商业分析中,不同的变量存在单位不同的问题,比如流量使用MB作为单位,而金额使用元作为单位,因此流量、金额无法直接进行比较;同时,单一指标采用不同单位也会无法直接比较,比如收入用元作单位和用万元作单位会在数值上相差很大。这样的差异性会强烈影响模型的结果,比如下例中的聚类方案(见图18-2)。
图18-2
同样的样本点,如果流量采用MB为单位,则A\B为一个簇,C\D为一个簇;如果使用GB为单位,则A\C一个簇,B\D一个簇。可见因为单位不同对模型的结果会产生颠覆性的影响。
为了消除字段间因为单位差异而导致模型不稳定的情况,需要将变量的单位消除,使得它们都是在一个“标准”的尺度上进行比较分析。因此需要采用标准化的技术,常用的方法包括极值标准化与学生标准化:
极差标准化
z-score标准化
极值标准化将数据映射到[0,1]之间,受极端值影响较大;学生标准化更多应用在对称分布的字段上(因为对称分布的均值有代表性),受极端值的影响较小,是多数模型的默认标准化方法。另外,这两种标准化方法都不会改变原字段分布图形的形态,仅仅是对数据进行了线性缩放而已。
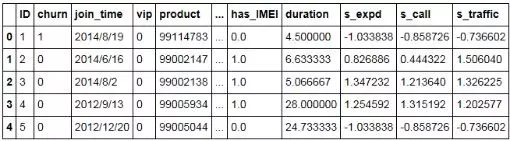
使用pandas提供的函数可以很方便地对字段进行标准化,使用scikit-learn也可以达到同样效果,而且在应用中可能更加方便,比如我们对已进行了对数转换的收入、通话时长、流量消费(接近正态分布)进行学生标准化的例子如下:
使用preprocessing.StandardScaler可以对多个字段一次性进行学生标准化,而且fit之后的转换器std_scaler可以重复使用。比如,使用训练集数据fit的转换器可以对测试集进行相同的转换(使用训练集的均值和标准差进行学生标准化)。
将标准化后的数据添加到数据集当中:
极值标准化的方法也类似:
在很多软件中,会在建模前默认对数据进行标准化,但并不是所有软件都如此,比如scikit-learn这样的开源工具。在scikit-learn中,部分模型会有用于标准化的参数选项(比如各种降维),另一些则需要手动进行标准化(例如逻辑回归、SVM等)。此外,并不是所有模型都需要预先进行数据标准化(比如决策树),而即便是同样的模型,运用在不同业务问题上也会有不同的标准化要求,这就要求我们对业务与模型都要深入了解才行。
规范化(Normalization)
标准化方法应用于列,规范化或称归一化一般应用于行。规范化是为了数据样本向量在做点乘运算或其他核函数计算相似性时,拥有统一的标准。如果将表中的每一行作为向量来看,规范化就是将其缩放成单位向量。
对于有n条记录m个字段的数据集,使用x代表行记录形成的m维向量,使用L2范数(这里L2范数就是欧几里德距离)进行规范化的公式为:
scikit-learn当中可以使用preprocessing.Normalizer对每一行进行规范化,仅仅是为了演示代码,我们将通信账单数据集的后三列提取出来,使用规范化方法进行转换如下:
可以发现转换后每个行向量都是单位长度,只是具有不同的角度。需要再次强调的是,本例仅为演示代码,因为对行执行规范化后,每列的分布形态会发生改变,因此不适用于本数据集。