图像特征描述子之ORB

原文站点：https://senitco.github.io/2017/07/09/image-feature-orb/

  ORB(Oriented FAST and Rotated BRIEF)算法是对FAST特征点检测和BRIEF特征描述子的一种结合，在原有的基础上做了改进与优化，使得ORB特征具备多种局部不变性，并为实时计算提供了可能。

特征点检测

  ORB首先利用FAST算法检测特征点，然后计算每个特征点的Harris角点响应值，从中筛选出 N 个最大的特征点，Harris角点的响应函数如下：

R=detM−α(traceM)2

相关内容已在博文 FAST角点检测和 Harris角点检测分别做了详细的介绍。
FAST检测特征点不具备尺度不变性，可以像SIFT特征一样，借助尺度空间理论构建图像高斯金字塔，然后在每一层金字塔图像上检测角点，以实现尺度不变性。对于旋转不变性，原论文中提出了一种利用图像矩(几何矩)，在半径为r的邻域内求取灰度质心的方法，从特征点到灰度质心的向量，定义为该特征点的主方向。图像矩定义如下：

mpq=Σx,yxpyqI(x,y),x,y∈[−r,r]

I(x,y) 表示像素灰度值，0阶矩 m00 即图像邻域窗口内所有像素的灰度和， m10 和 m01 分别相对 x 和相对 y 的一阶矩，因此图像局部邻域的中心矩或者质心可定义为

C=(m10m00,m01m00)

特征点与质心形成的向量与 X 轴的夹角定义为特征点的主方向

θ=arctan(m01,m10)

特征点描述

  ORB采用BRIEF作为特征描述方法，BRIEF虽然速度优势明显，但也存在一些缺陷，例如不具备尺度不变性和旋转不变性，对噪声敏感。尺度不变性的问题在利用FAST检测特征点时，通过构建高斯金字塔得以解决。BRIEF中采用 9×9 的高斯卷积核进行滤波降噪，可以在一定程度上缓解噪声敏感问题；ORB中利用积分图像，在 31×31 的Patch中选取随机点对，并以选取的随机点为中心，在 5×5 的窗口内计算灰度平均值(灰度和)，比较随机点对的邻域灰度均值，进行二进制编码，而不是仅仅由两个随机点对的像素值决定编码结果，可以有效地解决噪声问题。
  至于旋转不变性问题，可利用FAST特征点检测时求取的主方向，旋转特征点邻域，但旋转整个Patch再提取BRIEF特征描述子的计算代价较大，因此，ORB采用了一种更高效的方式，在每个特征点邻域Patch内，先选取256对随机点，将其进行旋转，然后做判决编码为二进制串。n个点对构成矩阵 S

S=[x1 y1x2y2……x2ny2n]

旋转矩阵 Rθ为

Rθ=[cosθ sinθ−sinθcosθ]

旋转后的坐标矩阵为

Sθ=RθS

描述子的区分性

  通过上述方法得到的特征描述子具有旋转不变性，称为steered BRIEF(sBRIEF)，但匹配效果却不如原始BRIEF算法，因为可区分性减弱了。特征描述子的一个要求就是要尽可能地表达特征点的独特性，便于区分不同的特征点。如下图所示，为几种特征描述子的均值分布，横轴为均值与0.5之间的距离，纵轴为相应均值下特征点的统计数量。可以看出，BRIEF描述子所有比特位的均值接近于0.5，且方差很大；方差越大表明可区分性越好。不同特征点的描述子表现出较大的差异性，不易造成无匹配。但steered BRIEF进行了坐标旋转，损失了这个特性，导致可区分性减弱，相关性变强，不利于匹配。

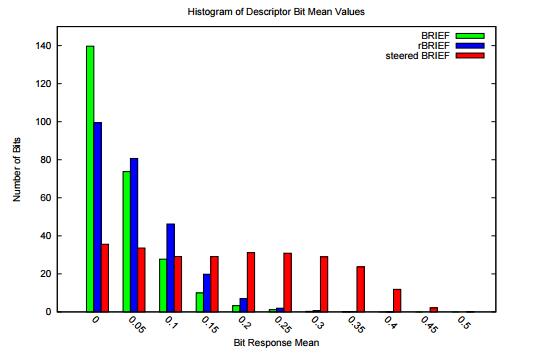
  为了解决steered BRIEF可区分性降低的问题，ORB使用了一种基于学习的方法来选择一定数量的随机点对。首先建立一个大约300k特征点的数据集(特征点来源于PASCAL2006中的图像)，对每个特征点，考虑其 31×31 的邻域Patch，为了去除噪声的干扰，选择 5×5 的子窗口的灰度均值代替单个像素的灰度，这样每个Patch内就有 N=(31−5+1)×(31−5+1)=27×27=729 个子窗口，从中随机选取2个非重复的子窗口，一共有 M=C2N 中方法。这样，每个特征点便可提取出一个长度为 M 的二进制串，所有特征点可构成一个 300k×M 的二进制矩阵 Q ，矩阵中每个元素取值为0或1。现在需要从 M 个点对中选取256个相关性最小、可区分性最大的点对，作为最终的二进制编码。筛选方法如下：
- 对矩阵 Q 的每一列求取均值，并根据均值与0.5之间的距离从小到大的顺序，依次对所有列向量进行重新排序，得到矩阵 T
- 将 T 中的第一列向量放到结果矩阵 R 中
- 取出 T 中的下一列向量，计算其与矩阵 R 中所有列向量的相关性，如果相关系数小于给定阈值，则将 T 中的该列向量移至矩阵 R 中，否则丢弃
- 循环执行上一步，直到 R 中有256个列向量；如果遍历 T 中所有列， R 中向量列数还不满256，则增大阈值，重复以上步骤。

这样，最后得到的就是相关性最小的256对随机点，该方法称为rBRIEF。

Experiment & Result

OpenCV实现ORB特征检测与描述

#include  
#include  
#include  
#include 

using namespace cv;

int main(int argc, char** argv) 
{ 
    Mat img_1 = imread("box.png"); 
    Mat img_2 = imread("box_in_scene.png");

    // -- Step 1: Detect the keypoints using STAR Detector 
    std::vector keypoints_1,keypoints_2; 
    ORB orb; 
    orb.detect(img_1, keypoints_1); 
    orb.detect(img_2, keypoints_2);

    // -- Stpe 2: Calculate descriptors (feature vectors) 
    Mat descriptors_1, descriptors_2; 
    orb.compute(img_1, keypoints_1, descriptors_1); 
    orb.compute(img_2, keypoints_2, descriptors_2);

    //-- Step 3: Matching descriptor vectors with a brute force matcher 
    BFMatcher matcher(NORM_HAMMING); 
    std::vector mathces; 
    matcher.match(descriptors_1, descriptors_2, mathces); 
    // -- dwaw matches 
    Mat img_mathes; 
    drawMatches(img_1, keypoints_1, img_2, keypoints_2, mathces, img_mathes); 
    // -- show 
    imshow("Mathces", img_mathes);

    waitKey(0); 
    return 0; 
}

OpenCV中ORB算法的部分源码实现

//计算Harris角点响应  
static void HarrisResponses(const Mat& img, vector& pts, int blockSize, float harris_k)  
{  
    CV_Assert( img.type() == CV_8UC1 && blockSize*blockSize <= 2048 );  

    size_t ptidx, ptsize = pts.size();  

    const uchar* ptr00 = img.ptr();  
    int step = (int)(img.step/img.elemSize1());  
    int r = blockSize/2;  

    float scale = (1 << 2) * blockSize * 255.0f;  
    scale = 1.0f / scale;  
    float scale_sq_sq = scale * scale * scale * scale;  

    AutoBuffer<int> ofsbuf(blockSize*blockSize);  
    int* ofs = ofsbuf;  
    for( int i = 0; i < blockSize; i++ )  
        for( int j = 0; j < blockSize; j++ )  
            ofs[i*blockSize + j] = (int)(i*step + j);  

    for( ptidx = 0; ptidx < ptsize; ptidx++ )  
    {  
        int x0 = cvRound(pts[ptidx].pt.x - r);  
        int y0 = cvRound(pts[ptidx].pt.y - r);  

        const uchar* ptr0 = ptr00 + y0*step + x0;  
        int a = 0, b = 0, c = 0;  

        for( int k = 0; k < blockSize*blockSize; k++ )  
        {  
            const uchar* ptr = ptr0 + ofs[k];  
            int Ix = (ptr[1] - ptr[-1])*2 + (ptr[-step+1] - ptr[-step-1]) + (ptr[step+1] - ptr[step-1]);  
            int Iy = (ptr[step] - ptr[-step])*2 + (ptr[step-1] - ptr[-step-1]) + (ptr[step+1] - ptr[-step+1]);  
            a += Ix*Ix;  
            b += Iy*Iy;  
            c += Ix*Iy;  
        }  
        pts[ptidx].response = ((float)a * b - (float)c * c -  harris_k * ((float)a + b) * ((float)a + b))*scale_sq_sq;  
    }  
}  

//计算FAST角点的主方向  
static float IC_Angle(const Mat& image, const int half_k, Point2f pt, const vector<int> & u_max)  
{  
    int m_01 = 0, m_10 = 0;  

    const uchar* center = &image.at (cvRound(pt.y), cvRound(pt.x));  

    // Treat the center line differently, v=0  
    for (int u = -half_k; u <= half_k; ++u)  
        m_10 += u * center[u];  

    // Go line by line in the circular patch  
    int step = (int)image.step1();  
    for (int v = 1; v <= half_k; ++v)  
    {  
        // Proceed over the two lines  
        int v_sum = 0;  
        int d = u_max[v];  
        for (int u = -d; u <= d; ++u)  
        {  
            int val_plus = center[u + v*step], val_minus = center[u - v*step];  
            v_sum += (val_plus - val_minus);  
            m_10 += u * (val_plus + val_minus);  
        }  
        m_01 += v * v_sum;  
    }  

    return fastAtan2((float)m_01, (float)m_10);  
}  


//计算ORB特征描述子
static void computeOrbDescriptor(const KeyPoint& kpt, const Mat& img, const Point* pattern, uchar* desc, int dsize, int WTA_K)  
{  
    float angle = kpt.angle;   
    //angle = cvFloor(angle/12)*12.f;  
    angle *= (float)(CV_PI/180.f);  
    float a = (float)cos(angle), b = (float)sin(angle);  

    const uchar* center = &img.at(cvRound(kpt.pt.y), cvRound(kpt.pt.x));  
    int step = (int)img.step;  

#if 1  
    #define GET_VALUE(idx) \       //取旋转后一个像素点的值  
        center[cvRound(pattern[idx].x*b + pattern[idx].y*a)*step + \  
               cvRound(pattern[idx].x*a - pattern[idx].y*b)]  
#else  
    float x, y;  
    int ix, iy;  
    #define GET_VALUE(idx) \ //取旋转后一个像素点，插值法  
        (x = pattern[idx].x*a - pattern[idx].y*b, \  
        y = pattern[idx].x*b + pattern[idx].y*a, \  
        ix = cvFloor(x), iy = cvFloor(y), \  
        x -= ix, y -= iy, \  
        cvRound(center[iy*step + ix]*(1-x)*(1-y) + center[(iy+1)*step + ix]*(1-x)*y + \  
                center[iy*step + ix+1]*x*(1-y) + center[(iy+1)*step + ix+1]*x*y))  
#endif  

    if( WTA_K == 2 )  
    {  
        for (int i = 0; i < dsize; ++i, pattern += 16)//每个特征描述子长度为32个字节  
        {  
            int t0, t1, val;  
            t0 = GET_VALUE(0); t1 = GET_VALUE(1);  
            val = t0 < t1;  
            t0 = GET_VALUE(2); t1 = GET_VALUE(3);  
            val |= (t0 < t1) << 1;  
            t0 = GET_VALUE(4); t1 = GET_VALUE(5);  
            val |= (t0 < t1) << 2;  
            t0 = GET_VALUE(6); t1 = GET_VALUE(7);  
            val |= (t0 < t1) << 3;  
            t0 = GET_VALUE(8); t1 = GET_VALUE(9);  
            val |= (t0 < t1) << 4;  
            t0 = GET_VALUE(10); t1 = GET_VALUE(11);  
            val |= (t0 < t1) << 5;  
            t0 = GET_VALUE(12); t1 = GET_VALUE(13);  
            val |= (t0 < t1) << 6;  
            t0 = GET_VALUE(14); t1 = GET_VALUE(15);  
            val |= (t0 < t1) << 7;  

            desc[i] = (uchar)val;  
        }  
    }  
    else if( WTA_K == 3 )  
    {  
        for (int i = 0; i < dsize; ++i, pattern += 12)  
        {  
            int t0, t1, t2, val;  
            t0 = GET_VALUE(0); t1 = GET_VALUE(1); t2 = GET_VALUE(2);  
            val = t2 > t1 ? (t2 > t0 ? 2 : 0) : (t1 > t0);  

            t0 = GET_VALUE(3); t1 = GET_VALUE(4); t2 = GET_VALUE(5);  
            val |= (t2 > t1 ? (t2 > t0 ? 2 : 0) : (t1 > t0)) << 2;  

            t0 = GET_VALUE(6); t1 = GET_VALUE(7); t2 = GET_VALUE(8);  
            val |= (t2 > t1 ? (t2 > t0 ? 2 : 0) : (t1 > t0)) << 4;  

            t0 = GET_VALUE(9); t1 = GET_VALUE(10); t2 = GET_VALUE(11);  
            val |= (t2 > t1 ? (t2 > t0 ? 2 : 0) : (t1 > t0)) << 6;  

            desc[i] = (uchar)val;  
        }  
    }  
    else if( WTA_K == 4 )  
    {  
        for (int i = 0; i < dsize; ++i, pattern += 16)  
        {  
            int t0, t1, t2, t3, u, v, k, val;  
            t0 = GET_VALUE(0); t1 = GET_VALUE(1);  
            t2 = GET_VALUE(2); t3 = GET_VALUE(3);  
            u = 0, v = 2;  
            if( t1 > t0 ) t0 = t1, u = 1;  
            if( t3 > t2 ) t2 = t3, v = 3;  
            k = t0 > t2 ? u : v;  
            val = k;  

            t0 = GET_VALUE(4); t1 = GET_VALUE(5);  
            t2 = GET_VALUE(6); t3 = GET_VALUE(7);  
            u = 0, v = 2;  
            if( t1 > t0 ) t0 = t1, u = 1;  
            if( t3 > t2 ) t2 = t3, v = 3;  
            k = t0 > t2 ? u : v;  
            val |= k << 2;  

            t0 = GET_VALUE(8); t1 = GET_VALUE(9);  
            t2 = GET_VALUE(10); t3 = GET_VALUE(11);  
            u = 0, v = 2;  
            if( t1 > t0 ) t0 = t1, u = 1;  
            if( t3 > t2 ) t2 = t3, v = 3;  
            k = t0 > t2 ? u : v;  
            val |= k << 4;  

            t0 = GET_VALUE(12); t1 = GET_VALUE(13);  
            t2 = GET_VALUE(14); t3 = GET_VALUE(15);  
            u = 0, v = 2;  
            if( t1 > t0 ) t0 = t1, u = 1;  
            if( t3 > t2 ) t2 = t3, v = 3;  
            k = t0 > t2 ? u : v;  
            val |= k << 6;  

            desc[i] = (uchar)val;  
        }  
    }  
    else  
        CV_Error( CV_StsBadSize, "Wrong WTA_K. It can be only 2, 3 or 4." );  

    #undef GET_VALUE  
}  

reference

• Paper: ORB: an efficient alternative to SIFT or SURF
• http://blog.csdn.net/hujingshuang/article/details/46984411
• http://blog.csdn.net/zouzoupaopao229/article/details/52625678
• https://segmentfault.com/a/1190000004200111
• http://www.cnblogs.com/ronny/p/4083537.html
• http://blog.csdn.net/luoshixian099/article/details/48523267
• http://blog.csdn.net/tiandijun/article/details/40679581