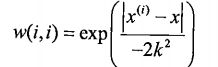《机器学习实战》学习笔记第八章 —— 线性回归、L1、L2范数正则项

 

相关笔记：

吴恩达机器学习笔记（一） —— 线性回归

吴恩达机器学习笔记（三） —— Regularization正则化

（

问题遗留：

小可只知道引入正则项能降低参数的取值，但为什么能保证 Σθ² <=λ ？

）

 

主要内容：

一.线性回归之普通最小二乘法

二.局部加权线性回归

三.岭回归（L2正则项）

四.lasso回归（L1正则项）

五.前向逐步回归

 

 

一.线性回归之普通最小二乘法

1.参数的值：（不带正则项）

2.Python代码：

def standRegres(xArr, yArr):    #普通最小二乘法（没有特征归一化），其实就是不带正则项的最小二乘法
    xMat = mat(xArr); yMat = mat(yArr).T
    xTx = xMat.T * xMat
    if linalg.det(xTx) == 0.0:      #如果方阵XTX的行列式为0，则不存在逆矩阵，所以结果不可求。
        print "This matrix is singular, cannot do inverse"
        return
    ws = xTx.I * (xMat.T * yMat)    #求出权值w，即参数
    return ws

 

 

二.局部加权线性回归

1.线性回归很容易出现欠拟合的现象，为了解决这个问题，我们可以使用局部加权线性回归。所谓“加权”，就是给每一个训练数据加上一个权值，而这个权值是根据训练数据点与测试数据点的远近而设定的。训练点离测试点越近，其权值越大；反之则反。

2.训练点 i 的权值 W(i, i) 为：

其中W为对角矩阵，对角线上的值就是数据点的权值。式子中k的值决定了测试点附近的点被赋予多大的权值，且k越小，附近点所占的权值越大，如图：

3.可求得参数的值为：

4.Python代码：

'''k决定了测试点附近的训练点被赋予多大的权值，k越小，权值越大'''
def lwlr(testPoint, xArr, yArr, k=1.0):     #局部加权线性回归（只能针对一个测试数据）
    xMat = mat(xArr); yMat = mat(yArr).T
    m = shape(xMat)[0]
    weights = mat(eye((m)))
    for j in range(m):  # next 2 lines create weights matrix
        diffMat = testPoint - xMat[j, :]  #
        weights[j, j] = exp(diffMat * diffMat.T / (-2.0 * k ** 2))
    xTx = xMat.T * (weights * xMat)
    if linalg.det(xTx) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testPoint * ws

def lwlrTest(testArr, xArr, yArr, k=1.0):  # 批量求局部加权线性回归（针对多个测试数据）
    m = shape(testArr)[0]
    yHat = zeros(m)
    for i in range(m):
        yHat[i] = lwlr(testArr[i], xArr, yArr, k)
    return yHat

5.拟合效果如图所示，可知当k越小时，对训练数据的拟合效果越好，但是“过好”的话就出现了过拟合，如第三幅图。而效果最好的当属第二幅图：

6.由上述分析以及代码可知，局部加权线性回归有个明显的弱点，那就是：对于每一个测试数据，都需要重新对训练数据集求出权值W，这个计算量应该挺大的。

 

 

三.岭回归

1.上述两种线性回归模型都是通过最小二乘法来求解参数的，但是最小二乘法要求矩阵X^TX存在逆矩阵，而这并不能保证。于是就有了“岭回归”。

2.所谓岭回归，其实就是在普通的损失函数上加上一个正则项，然而再对其用求导法，其损失函数和参数的值如下：

3.如上式子，听闻 (X^TX + λI) 的逆矩阵是必定存在的（除非λ=0），那么为什么通过引入正则项就可以使得其逆矩阵存在呢？

答：从感性上去理解，可知如果数据的特征比数据样本点还多，那么逆矩阵是求不出来的。而加入正则项之后，使得一些不重要的特征的参数接近于0或者等于0，这样就近似于把一些特征给“废掉”了。特征减少之后，可能就达到了特征数少于等于样本数的情况，从而使得逆矩阵可以被求出。

4.Python代码：

def regularize(xMat):  # 特征归一化
    inMat = xMat.copy()
    inMeans = mean(inMat, 0)  # calc mean then subtract it off
    inVar = var(inMat, 0)  # calc variance of Xi then divide by it
    inMat = (inMat - inMeans) / inVar
    return inMat

def ridgeRegres(xMat, yMat, lam=0.2):       #岭回归，其实就是加入了正则项的最小二乘法。能对XTX求逆，但还是需要进行判断。
    xTx = xMat.T * xMat
    denom = xTx + eye(shape(xMat)[1]) * lam
    if linalg.det(denom) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return
    ws = denom.I * (xMat.T * yMat)
    return ws

def ridgeTest(xArr, yArr):  #岭回归测试， 在30个不同的lambda下获得的参数
    xMat = mat(xArr); yMat = mat(yArr).T
    xMat = regularize(xMat)  # 特征归一化
    yMean = mean(yMat, 0)
    yMat = yMat - yMean  # to eliminate X0 take mean off of Y……不懂这一步的作用
    numTestPts = 30
    wMat = zeros((numTestPts, shape(xMat)[1]))
    for i in range(numTestPts): #h获取每个lambda下模型的参数
        ws = ridgeRegres(xMat, yMat, exp(i - 10))
        wMat[i, :] = ws.T
    return wMat

 

 

四.lasso回归

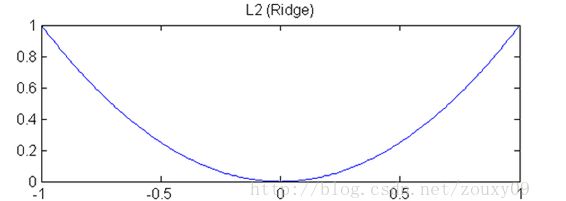
1.岭回归的正则项使用的平方项（有说法是L2范数，但L2范数不是在求完平方和之后还要开根吗？所以个人认为：岭回归的正则项是L2范数的平方），根据y=x^2的图像可知：

1）当|x|>1， 曲线的斜率很大，这就能加快梯度下降收敛的速度。

2）当|x|<=1时，斜率就变得非常小，此时正则项的作用可以说是失效的了，即不再具备惩罚参数的作用。

总和上述两点可知岭回归的特点是：能加速梯度下降的速度，且使得参数的值较小，但是不能直接把参数变成0（即使很接近0），这样岭回归的特征选取的功能就相对弱一些。

 

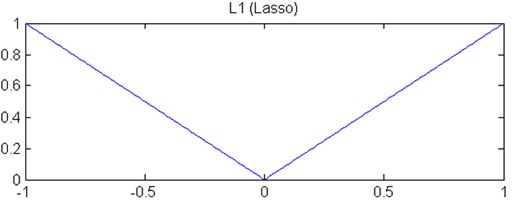
2.为了增强特征选取的功能，我们可以把岭回归的正则项换成是一次项绝对值，即L1范数：

可知y=|x|的图像如下：

1）曲线的斜率不会发生变化，也就是说正则项的乘法功效是恒定的，这也就使得梯度下降慢而稳定。

2）当|x|<=1时，相比y=x^2，y=|x|的斜率更大，这就使得把某些参数变成0成为了可能。所以lasso回归的特征选择的作用更加强大。

 

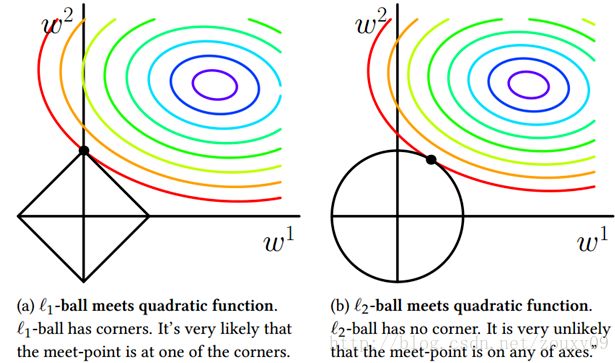
3.有一个数形结合的方法可以很好地解释为什么lasso回归比岭回归有更好的特征选取的作用。如下图：

其中左边的是lasso回归，右边的是岭回归。那一圈圈椭圆为目标函数（不知应该怎么叫，风险项？），而菱形和圆都为限制函数。其中交点就是我们最终求得的参数。

可知，椭圆与菱形的交点很容易出现在菱形的尖尖（顶点），而顶点位于坐标轴上，就是某个或者某些（多维的情况下）参数为0的情况，参数为0的那个特征就背废掉了。而圆与椭圆的交点要出现在坐标轴上的概率就没那么大了。所以lasso回归比岭回归有更好的特征选取的作用。

 

 

五.前向逐步回归

Python代码：

def regularize(xMat):  # 特征归一化
    inMat = xMat.copy()
    inMeans = mean(inMat, 0)  # calc mean then subtract it off
    inVar = var(inMat, 0)  # calc variance of Xi then divide by it
    inMat = (inMat - inMeans) / inVar
    return inMat

def rssError(yArr, yHatArr):  # 求出RSS残差平方和
    return ((yArr - yHatArr) ** 2).sum()

def stageWise(xArr, yArr, eps=0.01, numIt=100):     #前向逐步回归
    xMat = mat(xArr); yMat = mat(yArr).T
    xMat = regularize(xMat)     #归一化特征
    yMean = mean(yMat, 0)
    yMat = yMat - yMean  # can also regularize ys but will get smaller coef
    m, n = shape(xMat)
    ws = zeros((n, 1))
    for i in range(numIt):      #走numIt步，每一步从：所有的参数加一小部分或减一小部分 中选出RSS最小的那一个来更新参数
        lowestError = inf
        wsMax = ws.copy()       #用于保存当前步中RSS最小的那一组参数
        for j in range(n):      #枚举每一个参数
            for sign in [-1, 1]:    #-1为减 1为加
                wsTest = ws.copy()      #临时变量
                wsTest[j] += eps * sign
                yTest = xMat * wsTest
                rssE = rssError(yMat.A, yTest.A)
                if rssE < lowestError:      #更新当前步的最优参数组
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()   #更新最优参数组
    return ws

 

转载于:https://www.cnblogs.com/DOLFAMINGO/p/9489593.html