深度学习(二十六)——VAE
https://antkillerfarm.github.io/
VAE
变分自编码器(Variational Auto-Encoder,VAE)是Autoencoder的一种扩展。
论文:
《Auto-Encoding Variational Bayes》
以下部分主要摘自:
https://kexue.fm/archives/5253
变分自编码器(一):原来是这么一回事
分布变换
通常我们会拿VAE跟GAN比较,的确,它们两个的目标基本是一致的——希望构建一个从隐变量Z生成目标数据X的模型,但是实现上有所不同。更准确地讲,它们是假设了Z服从某些常见的分布(比如正态分布或均匀分布),然后希望训练一个模型 X = g ( Z ) X=g(Z) X=g(Z),这个模型能够将原来的概率分布映射到训练集的概率分布,也就是说,它们的目的都是进行分布之间的映射。
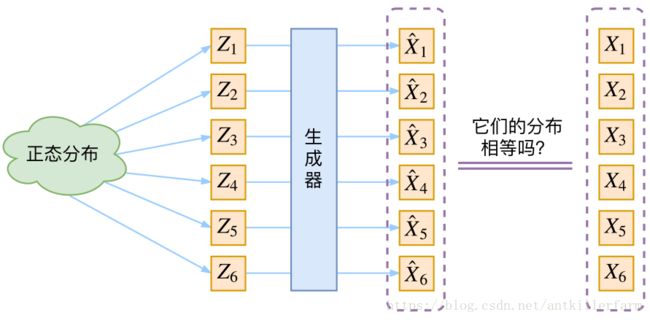
现在假设Z服从标准的正态分布,那么我就可以从中采样得到若干个 Z 1 , Z 2 , … , Z n Z_1, Z_2, \dots, Z_n Z1,Z2,…,Zn,然后对它做变换得到 X ^ 1 = g ( Z 1 ) , X ^ 2 = g ( Z 2 ) , … , X ^ n = g ( Z n ) \hat{X}_1 = g(Z_1),\hat{X}_2 = g(Z_2),\dots,\hat{X}_n = g(Z_n) X^1=g(Z1),X^2=g(Z2),…,X^n=g(Zn),我们怎么判断这个通过f构造出来的数据集,它的分布跟我们目标数据集的分布是不是一样的呢?
生成模型的难题就是判断生成分布与真实分布的相似度,因为我们只知道两者的采样结果,不知道它们的分布表达式。
有读者说不是有KL散度吗?当然不行,因为KL散度是根据两个概率分布的表达式来算它们的相似度的,然而目前我们并不知道它们的概率分布的表达式,我们只有一批从构造的分布采样而来的数据 { X ^ 1 , X ^ 2 , … , X ^ n } \{\hat{X}_1,\hat{X}_2,\dots,\hat{X}_n\} {X^1,X^2,…,X^n},还有一批从真实的分布采样而来的数据 { X 1 , X 2 , … , X n } \{X_1,X_2,\dots,X_n\} {X1,X2,…,Xn}(也就是我们希望生成的训练集)。我们只有样本本身,没有分布表达式,当然也就没有方法算KL散度。
虽然遇到困难,但还是要想办法解决的。GAN的思路很直接粗犷:既然没有合适的度量,那我干脆把这个度量也用神经网络训练出来吧。而VAE则使用了一个精致迂回的技巧。
VAE的传统理解
首先我们有一批数据样本 { X 1 , … , X n } \{X_1,\dots,X_n\} {X1,…,Xn},其整体用X来描述,我们本想根据 { X 1 , … , X n } \{X_1,\dots,X_n\} {X1,…,Xn}得到X的分布p(X),如果能得到的话,那我直接根据p(X)来采样,就可以得到所有可能的X了(包括 { X 1 , … , X n } \{X_1,\dots,X_n\} {X1,…,Xn}以外的),这是一个终极理想的生成模型了。当然,这个理想很难实现,于是我们将分布改一改:
p ( X ) = ∑ Z p ( X ∣ Z ) p ( Z ) p(X)=\sum_Z p(X|Z)p(Z) p(X)=Z∑p(X∣Z)p(Z)
此时 p ( X ∣ Z ) p(X\mid Z) p(X∣Z)就描述了一个由Z来生成X的模型,而我们假设Z服从标准正态分布,也就是 p ( Z ) = N ( 0 , I ) p(Z)=\mathcal{N}(0,I) p(Z)=N(0,I)。如果这个理想能实现,那么我们就可以先从标准正态分布中采样一个Z,然后根据Z来算一个X,也是一个很棒的生成模型。接下来就是结合自编码器来实现重构,保证有效信息没有丢失,再加上一系列的推导,最后把模型实现。框架的示意图如下:
看出了什么问题了吗?如果像这个图的话,我们其实完全不清楚:究竟经过重新采样出来的 Z k Z_k Zk,是不是还对应着原来的 X k X_k Xk,所以我们如果直接最小化 D ( X ^ k , X k ) 2 \mathcal{D}(\hat{X}_k,X_k)^2 D(X^k,Xk)2(这里D代表某种距离函数)是很不科学的,而事实上你看代码也会发现根本不是这样实现的。
VAE初现
其实,在整个VAE模型中,我们并没有去使用p(Z)(先验分布)是正态分布的假设,我们用的是假设 p ( Z ∣ X ) p(Z\mid X) p(Z∣X)(后验分布)是正态分布!!
具体来说,给定一个真实样本 X k X_k Xk,我们假设存在一个专属于 X k X_k Xk的分布 p ( Z ∣ X k ) p(Z\mid X_k) p(Z∣Xk)(学名叫后验分布),并进一步假设这个分布是(独立的、多元的)正态分布。为什么要强调“专属”呢?因为我们后面要训练一个生成器 X = g ( Z ) X=g(Z) X=g(Z),希望能够把从分布 p ( Z ∣ X k ) p(Z\mid X_k) p(Z∣Xk)采样出来的一个 Z k Z_k Zk还原为 X k X_k Xk。如果假设p(Z)是正态分布,然后从p(Z)中采样一个Z,那么我们怎么知道这个Z对应于哪个真实的X呢?现在 p ( Z ∣ X k ) p(Z\mid X_k) p(Z∣Xk)专属于 X k X_k Xk,我们有理由说从这个分布采样出来的Z应该要还原到 X k X_k Xk中去。
这样有多少个X就有多少个正态分布了。我们知道正态分布有两组参数:均值 μ \mu μ和方差 σ 2 \sigma^2 σ2(多元的话,它们都是向量),那我怎么找出专属于 X k X_k Xk的正态分布 p ( Z ∣ X k ) p(Z\mid X_k) p(Z∣Xk)的均值和方差呢?好像并没有什么直接的思路。那好吧,就用神经网络拟合出来吧!
于是我们构建两个神经网络 μ k = f 1 ( X k ) , log σ 2 = f 2 ( X k ) \mu_k = f_1(X_k),\log \sigma^2 = f_2(X_k) μk=f1(Xk),logσ2=f2(Xk)来算它们了。我们选择拟合 log σ 2 \log \sigma^2 logσ2而不是直接拟合 σ 2 \sigma^2 σ2,是因为 σ 2 \sigma^2 σ2总是非负的,需要加激活函数处理,而拟合 log σ 2 \log \sigma^2 logσ2不需要加激活函数,因为它可正可负。到这里,知道专属于 X k X_k Xk的均值和方差,也就知道它的正态分布长什么样了,然后从这个专属分布中采样一个 Z k Z_k Zk出来,经过一个生成器得到 X ^ k = g ( Z k ) \hat{X}_k=g(Z_k) X^k=g(Zk),现在我们可以放心地最小化 D ( X ^ k , X k ) 2 \mathcal{D}(\hat{X}_k,X_k)^2 D(X^k,Xk)2,因为 Z k Z_k Zk是从专属 X k X_k Xk的分布中采样出来的,这个生成器应该要把开始的 X k X_k Xk还原回来。
分布标准化
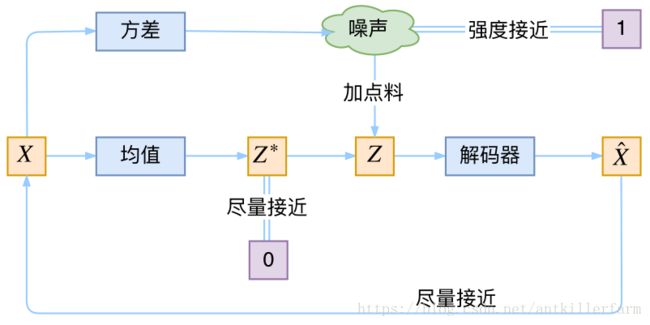
让我们来思考一下,根据上图的训练过程,最终会得到什么结果。
首先,我们希望重构X,也就是最小化 D ( X ^ k , X k ) 2 \mathcal{D}(\hat{X}_k,X_k)^2 D(X^k,Xk)2,但是这个重构过程受到噪声的影响,因为 Z k Z_k Zk是通过重新采样过的,不是直接由encoder算出来的。显然噪声会增加重构的难度,不过好在这个噪声强度(也就是方差)通过一个神经网络算出来的,所以最终模型为了重构得更好,肯定会想尽办法让方差为0。而方差为0的话,也就没有随机性了,所以不管怎么采样其实都只是得到确定的结果(也就是均值)。说白了,模型会慢慢退化成普通的AutoEncoder,噪声不再起作用。
为了使模型具有生成能力,VAE决定让所有的 p ( Z ∣ X ) p(Z\mid X) p(Z∣X)都向标准正态分布看齐。如果所有的 p ( Z ∣ X ) p(Z\mid X) p(Z∣X)都很接近标准正态分布 N ( 0 , I ) \mathcal{N}(0,I) N(0,I),那么根据定义:
p ( Z ) = ∑ X p ( Z ∣ X ) p ( X ) = ∑ X N ( 0 , I ) p ( X ) = N ( 0 , I ) ∑ X p ( X ) = N ( 0 , I ) p(Z)=\sum_X p(Z|X)p(X)=\sum_X \mathcal{N}(0,I)p(X)=\mathcal{N}(0,I) \sum_X p(X) = \mathcal{N}(0,I) p(Z)=X∑p(Z∣X)p(X)=X∑N(0,I)p(X)=N(0,I)X∑p(X)=N(0,I)
这样我们就能达到我们的先验假设:p(Z)是标准正态分布。然后我们就可以放心地从 N ( 0 , I ) \mathcal{N}(0,I) N(0,I)中采样来生成图像了。
那怎么让所有的 p ( Z ∣ X ) p(Z\mid X) p(Z∣X)都向 N ( 0 , I ) \mathcal{N}(0,I) N(0,I)看齐呢?如果没有外部知识的话,其实最直接的方法应该是在重构误差的基础上中加入额外的loss:
L μ = ∥ f 1 ( X k ) ∥ 2 , L σ 2 = ∥ f 2 ( X k ) ∥ 2 \mathcal{L}_{\mu}=\Vert f_1(X_k)\Vert^2,\mathcal{L}_{\sigma^2}=\Vert f_2(X_k)\Vert^2 Lμ=∥f1(Xk)∥2,Lσ2=∥f2(Xk)∥2
因为它们分别代表了均值 μ k \mu_k μk和方差的对数 log σ 2 \log \sigma^2 logσ2,达到 N ( 0 , I ) \mathcal{N}(0,I) N(0,I)就是希望二者尽量接近于0了。不过,这又会面临着这两个损失的比例要怎么选取的问题,选取得不好,生成的图像会比较模糊。所以,原论文直接算了一般(各分量独立的)正态分布与标准正态分布的KL散度 K L ( N ( μ , σ 2 ) ∥ N ( 0 , I ) ) KL\Big(N(\mu,\sigma^2)\Big\Vert N(0,I)\Big) KL(N(μ,σ2)∥∥∥N(0,I))作为这个额外的loss,计算结果为:
L μ , σ 2 = 1 2 ∑ i = 1 d ( μ ( i ) 2 + σ ( i ) 2 − log σ ( i ) 2 − 1 ) \mathcal{L}_{\mu,\sigma^2}=\frac{1}{2} \sum_{i=1}^d \Big(\mu_{(i)}^2 + \sigma_{(i)}^2 - \log \sigma_{(i)}^2 - 1\Big) Lμ,σ2=21i=1∑d(μ(i)2+σ(i)2−logσ(i)2−1)
这里的d是隐变量Z的维度,而 μ ( i ) \mu_{(i)} μ(i)和 σ ( i ) 2 \sigma_{(i)}^2 σ(i)2分别代表一般正态分布的均值向量和方差向量的第i个分量。直接用这个式子做补充loss,就不用考虑均值损失和方差损失的相对比例问题了。显然,这个loss也可以分两部分理解:
L μ , σ 2 = L μ + L σ 2 L μ = 1 2 ∑ i = 1 d μ ( i ) 2 = 1 2 ∥ f 1 ( X ) ∥ 2 L σ 2 = 1 2 ∑ i = 1 d ( σ ( i ) 2 − log σ ( i ) 2 − 1 ) \begin{aligned}&\mathcal{L}_{\mu,\sigma^2}=\mathcal{L}_{\mu} + \mathcal{L}_{\sigma^2}\\ &\mathcal{L}_{\mu}=\frac{1}{2} \sum_{i=1}^d \mu_{(i)}^2=\frac{1}{2}\Vert f_1(X)\Vert^2\\ &\mathcal{L}_{\sigma^2}=\frac{1}{2} \sum_{i=1}^d\Big(\sigma_{(i)}^2 - \log \sigma_{(i)}^2 - 1\Big)\end{aligned} Lμ,σ2=Lμ+Lσ2Lμ=21i=1∑dμ(i)2=21∥f1(X)∥2Lσ2=21i=1∑d(σ(i)2−logσ(i)2−1)
Reparameterization Trick
这是实现模型的一个技巧。我们要从 p ( Z ∣ X k ) p(Z\mid X_k) p(Z∣Xk)中采样一个 Z k Z_k Zk出来,尽管我们知道了 p ( Z ∣ X k ) p(Z\mid X_k) p(Z∣Xk)是正态分布,但是均值方差都是靠模型算出来的,我们要靠这个过程反过来优化均值方差的模型,但是“采样”这个操作是不可导的,而采样的结果是可导的,于是我们利用了一个事实:
从 N ( μ , σ 2 ) \mathcal{N}(\mu,\sigma^2) N(μ,σ2)中采样一个Z,相当于从 N ( 0 , I ) \mathcal{N}(0,I) N(0,I)中采样一个 ε \varepsilon ε,然后让 Z = μ + ε × σ Z=\mu + \varepsilon \times \sigma Z=μ+ε×σ。
于是,我们将从 N ( μ , σ 2 ) \mathcal{N}(\mu,\sigma^2) N(μ,σ2)采样变成了从 N ( 0 , I ) \mathcal{N}(0,I) N(0,I)中采样,然后通过参数变换得到从 N ( μ , σ 2 ) \mathcal{N}(\mu,\sigma^2) N(μ,σ2)中采样的结果。这样一来,“采样”这个操作就不用参与梯度下降了,改为采样的结果参与,使得整个模型可训练了。
VAE本质
VAE本质上就是在我们常规的自编码器的基础上,对encoder的结果(在VAE中对应着计算均值的网络)加上了“高斯噪声”,使得结果decoder能够对噪声有鲁棒性;而那个额外的KL loss(目的是让均值为0,方差为1),事实上就是相当于对encoder的一个正则项,希望encoder出来的东西均有零均值。
那另外一个encoder(对应着计算方差的网络)的作用呢?它是用来动态调节噪声的强度的。直觉上来想,当decoder还没有训练好时(重构误差远大于KL loss),就会适当降低噪声(KL loss增加),使得拟合起来容易一些(重构误差开始下降);反之,如果decoder训练得还不错时(重构误差小于KL loss),这时候噪声就会增加(KL loss减少),使得拟合更加困难了(重构误差又开始增加),这时候decoder就要想办法提高它的生成能力了。
简言之,重构的过程是希望没噪声的,而KL loss则希望有高斯噪声的,两者是对立的。所以,VAE跟GAN一样,内部其实是包含了一个对抗的过程,只不过它们两者是混合起来,共同进化的。
VAE vs AE
VAE和AE的差异在于:
1.两者虽然都是X->Z->X’的结构,但是AE寻找的是单值映射关系,即: z = f ( x ) z=f(x) z=f(x)。
2.而VAE寻找的是分布的映射关系,即: D X → D Z D_X\to D_Z DX→DZ。
为什么会有这个差别呢?我们不妨从生成模型的角度考虑一下。既然AE的decoder做的是Z->X’的变换,那么理论上它也可以作为生成器使用。但这里有个问题,显然不是所有的 R Z R^Z RZ都是有效的Z,或者可以说Z只占了高维空间 R Z R^Z RZ的一部分。Z的边界在哪里?如何得到有效的z,从而生成x?这些都不是AE能解决的。
VAE映射的是分布,而分布可以通过采样得到有效的z,从而生成相应的x。