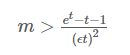大数据下的基数估计(Linear Counting,LogLog Counting,HyperLogLog Counting,Adaptive Counting)

基数估计

缘起

项目中遇到的问题，考虑如下场景：

A,B,C,…..N个集合，这里的集合不是严格意义上的集合，只是指一个list，里面有重复元素。

然后我要统计这些集合的交集，并集的集合（这里的交集并集为严格意义上的集合，无重复元素）的数量，即先做 inner join 后，再 count(distinct())。

这些集合的大小从十万到十亿不等，大概有几百个这样的集合。

目前是通过mapreduce来进行计算。

下一个任务，又会重复计算这些交集

问题

1.内存资源紧张，磁盘IO消耗主要时间。
2.重复计算某些集合之间的join。

改进

1.避免大集合之间做join
2.避免重复任务

新方法

1.对每个集合进行基数统计。
2.保存各个集合的基数统计的中间结果，每个大概为几k到几十k。
3.对中间结果进行交集和并集的计算，估计基数值。

基本的概念我就不写了，基本上这篇博客介绍的很清楚：

http://blog.codinglabs.org/tag.html#基数估计

另外原作者的论文我觉得写得非常好，谷歌的改进算法原论文也写得很好

从简单到复杂

Linear Counting

Linear Counting（简称LC）是最基本的概率模型的基数统计方法，之后的LogLogCounting（简称LLC）和HyperLogLog Counting（HLLC）的统计思想都是来源于这个统计方法进行的改进。

以下直接摘自上面说的那篇博客：

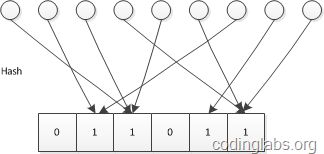
LC的基本思路是：设有一哈希函数H，其哈希结果空间有m个值（最小值0，最大值m-1），并且哈希结果服从均匀分布。使用一个长度为m的bitmap，每个bit为一个桶，均初始化为0，设一个集合的基数为n，此集合所有元素通过H哈希到bitmap中，如果某一个元素被哈希到第k个比特并且第k个比特为0，则将其置为1。当集合所有元素哈希完成后，设bitmap中还有u个bit为0。则：
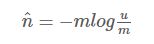
为n的一个估计，且为最大似然估计（MLE）。
误差分析：

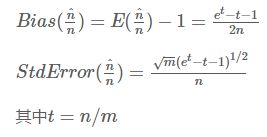
LC原理图：

具体推导就不写了，感兴趣参见原博客。

下面分析复杂度：

其实LC算法和bitmap算法很相似，都是一个bit存储一个信息，故空间复杂度为O(Nmax）

误差控制：

从上面那个公式可以反推出：

LogLog Counting

LogLogCounting ,顾名思义，空间复杂度只有O(loglogN)了，这也太牛了吧。

公式，推导，还在整理，目前我只整理了测试报告，包含实现基本步骤，和性能测试结果。

算法基本说明：
设：

元素名称	说明
N	基数上限值
a	A集合中某一元素
b	B集合中某一元素
Hash()	某种hash函数
L	某BitMap
E	估计的基数值
m	BitMap的长度
u	Bitmap中0的数量
f(L)	Bitmap中，从左到右第一个1出现的位置

BitMap：非概率算法。

算法步骤：
1.生成长度为N的BitMap:L。
2.hash（a）到L中某一位，并置为1.
3.将输入集合重复第2步。
4.估计值E 等于L中1的个数。

LinearCounting：概率算法。

算法步骤：
生成长度为m的BitMap：L。
hash(a)到L中某一位，并置为1.
将输入集合重复第2步.
统计BitMap中0的数量为u，则估计值E = -mlog(u/m)

LogLogCounting: 概率算法。

算法步骤：
生成长度为m的BitMap：L。其中m=32，并生成2^k个寄存器M，k

AdaptiveCounting: 概率算法。

算法步骤：
采用LogLogCounting 计算，然后计算空桶率b.
如果b<0.051，则采用LogLogCounting估计公式,否则采用LinearCounting估计公式.

HyperLogLogCounting: 概率算法。

算法步骤：
前四步和LogLogCounting前四步相同。
估计值变为E =  ，其中 ，即将算数平均替换为调和平均。
分段偏差修正：

E ≤ 5/2 m ,                使用LC估计.
5/2 m < E ≤1/30 2^32 ,        使用E估计.
E > 1/30 2^32  ,              使用 E = -2^32 log⁡(1-E/2^32 ) 估计.

HyperLogLog++: 概率算法。

算法步骤：

    将HyperLogLog中32位bitmap变为64位。
    增加M的稀疏表示，用键值对替代M。
    分段偏差修正：
        E ≤ 5m ,                E’=(E-bias(E,p)).
        E > 5m ,                  E’ = E 
        V ≠0,                   使用LC估计,H = LC(m,V)
        V = 0,                  H = E’
        H ≤Threshold(p)     return H
        H >Threshold(p)     return E’

MinHash: 概率算法。

算法步骤：
将Hash(A),hash(B),最小的k个值分别放入集合S1，S2。
求Jaccard Index : J = y/k, 其中，y= |S1∩S2|

HyperLogLog++&Inclusion-exculsion principle: 概率算法。

算法步骤：
利用HyperLogLog++分别计算|A|,|B|, |A∪B| 的基数
利用 Inclusion-exculsion principle ： |A∩B| = |A| + |B| - |A∪B|

HyperLogLog++&MinHash: 概率算法。

算法步骤：
利用HyperLogLog++计算两个集合并集的基数x=|A∪B|
利用MinHash计算 Jaccard Index：J
由J=(|A∩B|)/(|A∪B|) , 得到实际基数y = |A∩B|= J * x