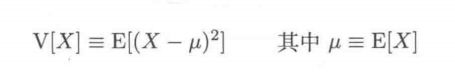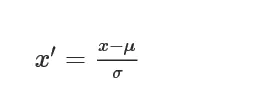期望、方差、标准差、标准化、归一化
序
我在看关于KNN的算法介绍里面的时候，提到欧氏距离的时候，说它的缺点的时候，提到了方差，提到了归一化、标准化。如果你也没明白，希望通过本文能理解这个含义。我对上来就直接贴一个数学公式感到头大。
一 期望值
这都是概率论的知识点，不是数学专业，所以侧重于理解，没有公理来证明。目的为了把抽象的概念转换为集合、数字、函数等已知的数学概念，便于理解问题。
一些基础的概念如：样本空间Ω、事件、随机变量、概率、联合概率、条件概率等，请参照百科的《概率论》。
一个练习题 ：
一副扑克牌，除掉大小王外还有52张。重新洗牌后，随机抽取一张，颜色记为X，再抽取一张，颜色记为Y，问X\Y相同的概率有多大？
p(X,Y同一种颜色)=P(X=红，Y=红色)+P(X=黑，Y=黑)
= P(Y=红|X=红)*P(X=红)+P(Y=黑|X=黑)*P(X=黑)
= 25/51*1/2+25/51*1/2=25/51
下面从期望值开始：
数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。需要注意的是，期望值并不一定等同于常识中的“期望”——“期望值”也许与每一个结果都不相等。期望值是该变量输出值的平均数。期望值并不一定包含于变量的输出值集合里。
对于离散型：
离散型随机变量的一切可能的取值 与对应的概率 乘积之和称为该离散型随机变量的数学期望 [2] (若该求和绝对收敛），记为 。它是简单算术平均的一种推广，类似加权平均。
离散型随机变量X的取值为 
， 
为X对应取值的概率，可理解为数据 出现的频率 ，则：
举个例子：例如，美国赌场中经常用的轮盘上有38个数字，每一个数字被选中的几率都是相等的。赌注一般压在其中某一个数字上，如果轮盘的输出值和这个数字相等，那么下赌者可以将相当于赌注35倍的奖金和原赌注拿回（总共是原赌注的36倍），若输出值和下压数字不同，则赌注就输掉了。因此，如果赌注是1美元的话，这场赌博的期望值是：
, 结果是 1-2/38= 0.947也就是说，平均起来每赌一次就会输掉5.3美分。
对于连续型
如果X是连续的随机变量，存在一个相应的概率密度函数 ，若积分
绝对收敛，那么 的期望值可以计算为：
是针对于连续的随机变量的，与离散随机变量的期望值的算法同出一辙，由于输出值是连续的，所以把求和改成了积分。
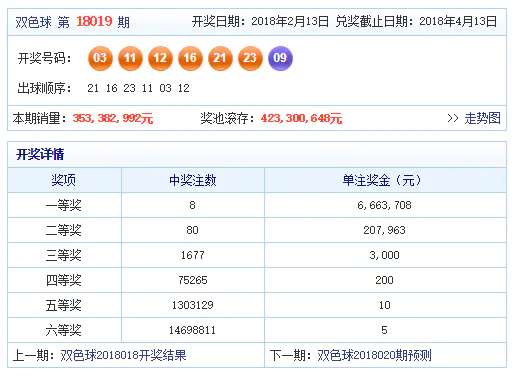
做个练习：国内彩票对于双色球可能大家都不陌生，那么根据公开资料可以计算下它的期望值。
如果你算完了，也就深刻理解了它为啥叫做智商税了。
二 方差
即使上面引入了期望值，它用于描述分布性质的主要特征，还是无法判断数据的离散的情况，又引入方差的指标，方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。
离散型
在概率分布中，设X是一个离散型随机变量，若E{[X-E（X）]^2}存在，则称E{[X-E（X）]^2}为X的方差，记为D（X），Var（X）或V（X），其中E（X）是X的期望值，X是变量值 [1] ，公式中的E是期望值expected value的缩写，意为“变量值与其期望值之差的平方和”的期望值。 [2] 离散型随机变量方差计算公式：
V（X）=E{[X-E（X）]^2}=E（X^2） - [ E（X）]^2
设E[X]的期望值E[X]=μ.根据定义方差必然为非负。
连续型：
todo.
三 标准差
由于方差是数据的平方，与检测值本身相差太大，人们难以直观的衡量。举个例子，假设X标识飞行距离m，而方差V[X]就是距离之差的平方
,如果表示长度，则方差是长度的平方，无法直接比较。所以通过平方根运算把它还原为![\sqrt[m^{2}]{}](http://img.e-com-net.com/image/info8/9010ed33e1db46698c4deb9463318036.gif){kind=small}
.这就是我们要说的标准差。
在统计学中样本的均差多是除以自由度（n-1），它是意思是样本能自由选择的程度。当选到只剩一个时，它不可能再有自由了，所以自由度是n-1。
另外，常见的说法是记方差为
σ平方
。
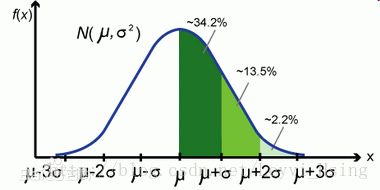
举个例子：一个班级里有60个学生，平均成绩是70分，标准差是9，方差是81，成绩服从正态分布，那么我们通过方差不能直观的确定班级学生与均值到底偏离了多少分，通过标准差我们就很直观的得到学生成绩分布在[61,79]范围的概率为0.6826，即约等于下图中的34.2%*2
四 归一化与标准化
我们在对于收集到的数据进行处理之前，通常进行一些标准化处理，比如处理不同的难度考试成绩一如偏差值，处理奥运比赛奖牌数引入权重数处理金银铜牌的权重，本质上也是一种标准化。
如果是转化为图表的表示，计算图表的欧式距离来计算相似性。这里就用到了特征缩放（Feature scaling），特征缩放（Feature Scaling）是将不同特征的值量化到同一区间的方法。
归一化(Normalization)
常用的方法是通过对原始数据进行线性变换把数据映射到[0,1]之间。
min-max normalization：
其中minmin是样本中最小值，maxmax是样本中最大值，注意在数据流场景下最大值与最小值是变化的。另外，最大值与最小值非常容易受异常点影响，所以这种方法鲁棒性较差，只适合传统精确小数据场景。
其他的还有：
2. 对数函数转换
y=log10(x)
3.反余切函数转换
y=atan(x)*2/PI
标准化(Standardization)：
将数据标准化处理之后，均值变为0，方差变为1，即服从标准正态分布。
常用z-score标准化：
y=(x-μ)/σ 
一般来说z-score不是归一化，而是标准化，归一化只是标准化的一种。
其中μ是样本的均值，σ是样本的标准差，它们可以通过现有样本进行估计。在已有样本足够多的情况下比较稳定，适合现代嘈杂大数据场景。特别适用于数据的最大值和最小值未知，或存在孤立点。
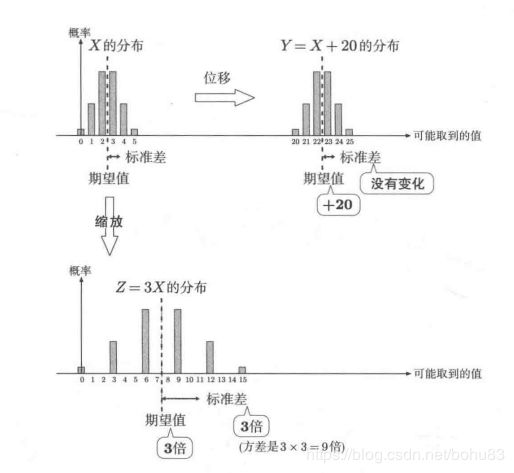
为什么z-score 标准化后的数据标准差为1?
这里涉及标准差的计算，
增加常量c之后,标准差不变。
乘以常量c之后，标准差变为|c|倍。
怎么选择？
归一化是为了消除不同数据之间的量纲，方便数据比较和共同处理。标准化是为了方便数据的下一步处理，而进行的数据缩放等变换，把所有维度的变量一视同仁，在最后计算距离中发挥相同的作用。这里只是参考别人的意见，没有实地动手处理过真正的项目数据，仅供参考。以实地效果为准。
- 如果对输出结果范围有要求，用归一化。
- 如果数据较为稳定，不存在极端的最大最小值，用归一化。
- 如果数据存在异常值和较多噪音，用标准化，可以间接通过中心化避免异常值和极端值的影响。
其他 常用公式
V[X]= ![E[X^{2}]](http://img.e-com-net.com/image/info8/bf8080bb10114356bc84d4db91b679b8.gif){kind=small}
- ![E[X]^{2}](http://img.e-com-net.com/image/info8/ab9bc1f84f3f4f618fb7dc5b8c582875.gif){kind=small}
或者 =
其中μ=E[X],
=V[X].
就是说X平方的期望值=X期望值的平方+X的方差。
参考：
http://dengxinbo.cn/2019/01/07/%E5%BD%92%E4%B8%80%E5%8C%96%E5%92%8C%E6%A0%87%E5%87%86%E5%8C%96%E4%BB%A5%E5%8F%8A%E6%AC%A7%E6%B0%8F%E8%B7%9D%E7%A6%BB/
https://blog.csdn.net/pipisorry/article/details/52247379