R语言 一元线性回归、多元线性、多项式回归

关注微信号：小程在线

关注CSDN博客：程志伟的博客

R版本：3.6.1

本节主要介绍了一元线性回归、多元线性、多项式回归。

重点介绍了summary里面每个参数的意义；

创建训练集、测试集；

多项式poly()函数以及I()函数的使用。

###########一元线性回归#############

> library(MASS)
> data(Boston)    # 506 obs and 14 variables
> names(Boston)
 [1] "crim"    "zn"      "indus"   "chas"    "nox"     "rm"      "age"    
 [8] "dis"     "rad"     "tax"     "ptratio" "black"   "lstat"   "medv"   

使用 lm()来拟合数据模型

> lm1 <- lm(medv ~ rm, data=Boston)
> lm1

Call:
lm(formula = medv ~ rm, data = Boston)

Coefficients:
(Intercept)           rm  
    -34.671        9.102  

> summary(lm1)

Call:
lm(formula = medv ~ rm, data = Boston)

Residuals:
    Min      1Q  Median      3Q     Max 
-23.346  -2.547   0.090   2.986  39.433 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -34.671      2.650  -13.08   <2e-16 ***
rm             9.102      0.419   21.72   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 6.616 on 504 degrees of freedom
Multiple R-squared:  0.4835,    Adjusted R-squared:  0.4825 
F-statistic: 471.8 on 1 and 504 DF,  p-value: < 2.2e-16

#Estimate 表示估计系数
# Std. Error表示估计系数的差异性，这个值要比估计系数小一个数量级
#t value 表示用于变量的回归系数是否对模型有帮助
#Pr(>|t|)  变量之间不相关的概率，这个值越小越好
# **** 表示显著性，*越多越显著

> summary(lm1)$coefficients
              Estimate Std. Error   t value     Pr(>|t|)
(Intercept) -34.670621  2.6498030 -13.08423 6.950229e-34
rm            9.102109  0.4190266  21.72203 2.487229e-74

#残差是正态分布的，意味着预测值和实际值之间的差异接近 0

> summary(lm1)$residuals[1:20]
         1          2          3          4          5          6          7 
-1.1757458 -2.1740210  3.9719677  4.3740621  5.8178479  4.8440600  2.8487416 
         8          9         10         11         12         13         14 
 5.5924041 -0.0833549 -1.0784415 -8.3735282 -1.1239521  2.7683010  0.9221744 
        15         16         17         18         19         20 
-2.6158356  1.4689170  3.7496040 -2.3510120  5.2095142  0.7428426 

#评估模型拟合得好不好的标准,决定系数为 1 时，拟合程度最好

> summary(lm1)$r.squared
[1] 0.4835255

#如果值超过 1，意味着它们之间有关联

> summary(lm1)$fstatistic
   value    numdf    dendf 
471.8467   1.0000 504.0000 

#线性模型 lm1 使用 predict()函数

> newdata <- data.frame(rm=6)
> predict(lm1, newdata)
       1 
19.94203 

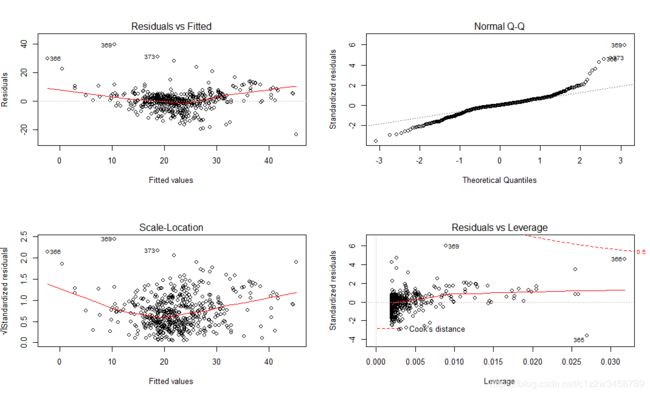
#第一张图是标准的残差曲线图，展示了拟合值下的残差。一些趋于异常值的点在图中标注了出来
#第二张图是残差的正态百分位数图,残差是正态分布的
#最后一张图展示了残差 vs.杠杆比率。在这张图中有标记的点表示我们可能想要审查的可疑情况

> par(mfrow=c(2,2))
> plot(lm1)

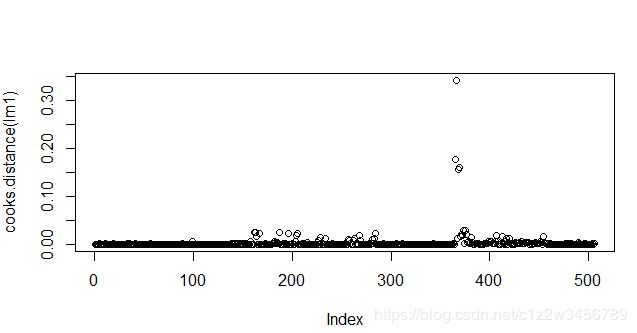
#cook距离可以看出数据点的异常值
> par(mfrow=c(1,1))
> plot(cooks.distance(lm1))

> ###########多元线性回归#################
> library(car)
> data(Prestige)
> summary(Prestige)
   education          income          women           prestige    
 Min.   : 6.380   Min.   :  611   Min.   : 0.000   Min.   :14.80  
 1st Qu.: 8.445   1st Qu.: 4106   1st Qu.: 3.592   1st Qu.:35.23  
 Median :10.540   Median : 5930   Median :13.600   Median :43.60  
 Mean   :10.738   Mean   : 6798   Mean   :28.979   Mean   :46.83  
 3rd Qu.:12.648   3rd Qu.: 8187   3rd Qu.:52.203   3rd Qu.:59.27  
 Max.   :15.970   Max.   :25879   Max.   :97.510   Max.   :87.20  
     census       type   
 Min.   :1113   bc  :44  
 1st Qu.:3120   prof:31  
 Median :5135   wc  :23  
 Mean   :5402   NA's: 4  
 3rd Qu.:8312            
 Max.   :9517            
> head(Prestige)
                    education income women prestige census type
gov.administrators      13.11  12351 11.16     68.8   1113 prof
general.managers        12.26  25879  4.02     69.1   1130 prof
accountants             12.77   9271 15.70     63.4   1171 prof
purchasing.officers     11.42   8865  9.11     56.8   1175 prof
chemists                14.62   8403 11.68     73.5   2111 prof
physicists              15.64  11030  5.13     77.6   2113 prof
> #c创建新的数据集
> Prestige_noNA <- na.omit(Prestige)
> n <- nrow(Prestige_noNA)  # Number of observations = 102
> ntrain <- round(n*0.6)    # 60% for training set
> set.seed(333)             # Set seed for reproducible results
> tindex <- sample(n, ntrain) # Create an index
> trainPrestige <- Prestige_noNA[tindex,]  # Create training set
> testPrestige <- Prestige_noNA[-tindex,]  # Create test set

> #查看变量与因变量的关系
> plot(trainPrestige$prestige, trainPrestige$education) #Trend
> plot(trainPrestige$prestige, trainPrestige$income) #No trend
> plot(trainPrestige$prestige, trainPrestige$women) #No trend
> #线性回归
> lm2 <- lm(prestige～., data=trainPrestige)
Error: unexpected input in "lm2 <- lm(prestige?
> #线性回归
> lm2 <- lm(prestige ~., data=trainPrestige)
> summary(lm2)

Call:
lm(formula = prestige ~ ., data = trainPrestige)

Residuals:
     Min       1Q   Median       3Q      Max 
-13.7864  -4.0290   0.8807   4.5369  16.9482 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.544e+01  9.901e+00  -1.560  0.12492    
education    4.562e+00  8.320e-01   5.483 1.24e-06 ***
income       9.607e-04  3.204e-04   2.999  0.00415 ** 
women        7.252e-03  4.543e-02   0.160  0.87379    
census       1.031e-03  7.390e-04   1.396  0.16876    
typeprof     5.981e+00  5.773e+00   1.036  0.30495    
typewc      -1.137e+00  3.962e+00  -0.287  0.77531    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 7.145 on 52 degrees of freedom
Multiple R-squared:  0.8406,    Adjusted R-squared:  0.8222 
F-statistic: 45.71 on 6 and 52 DF,  p-value: < 2.2e-16

> plot(lm2$fitted, lm2$residuals)
> #预测
> predict2 <- predict(lm2, newdata=testPrestige)
> #相关性
> cor(predict2, testPrestige$prestige)
[1] 0.9151361
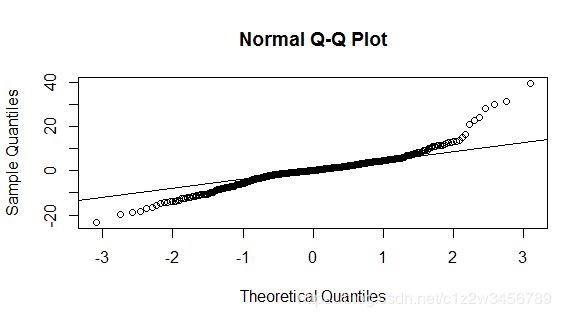
> rs <- residuals(lm1)
> qqnorm(rs)
> qqline(rs)

> library(MASS)
> data(Boston)
> names(Boston)
 [1] "crim"    "zn"      "indus"   "chas"    "nox"     "rm"     
 [7] "age"     "dis"     "rad"     "tax"     "ptratio" "black"  
[13] "lstat"   "medv"   
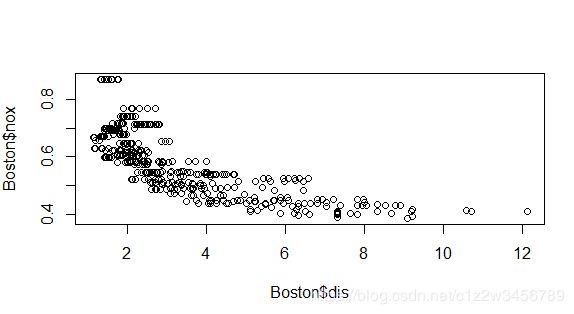
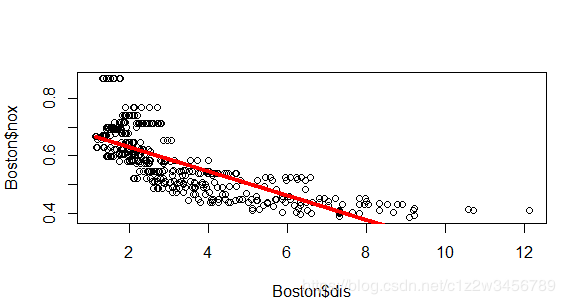
> # Scatterplot to show curvilinearity of data
> plot(Boston$dis, Boston$nox)

> # Fit simple model first
> fit_d1 <- lm(nox ~ dis, data=Boston)
> summary(fit_d1)

Call:
lm(formula = nox ~ dis, data = Boston)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.12239 -0.05212 -0.01257  0.04391  0.23041 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.715343   0.006796  105.26   <2e-16 ***
dis         -0.042331   0.001566  -27.03   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.07412 on 504 degrees of freedom
Multiple R-squared:  0.5917,    Adjusted R-squared:  0.5909 
F-statistic: 730.4 on 1 and 504 DF,  p-value: < 2.2e-16

> plot(Boston$dis, Boston$nox)
> lines(Boston$dis, fit_d1$fitted.values, col=2, lwd=3)

> # Fit model to predict nox (nitrogen oxides concentration)
> # using polynomial degree 2 with dis (distances to emp centers)
> fit_d2 <- lm(nox ~ poly(dis, 2, raw=TRUE), data=Boston)
> summary(fit_d2)

Call:
lm(formula = nox ~ poly(dis, 2, raw = TRUE), data = Boston)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.129559 -0.044514 -0.007753  0.025778  0.201882 

Coefficients:
                           Estimate Std. Error t value Pr(>|t|)    
(Intercept)                0.843991   0.011196   75.39   <2e-16 ***
poly(dis, 2, raw = TRUE)1 -0.111628   0.005320  -20.98   <2e-16 ***
poly(dis, 2, raw = TRUE)2  0.007135   0.000530   13.46   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.06361 on 503 degrees of freedom
Multiple R-squared:  0.6999,    Adjusted R-squared:  0.6987 
F-statistic: 586.4 on 2 and 503 DF,  p-value: < 2.2e-16

> plot(Boston$dis, Boston$nox)
> lines(sort(Boston$dis), fit_d2$fitted.values[order(Boston$dis)], col = 2, lwd = 3)

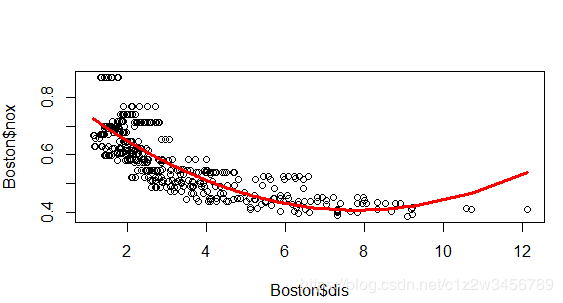
> # Fit model to predict nox (nitrogen oxides concentration)
> # using polynomial degree 3 with dis (distances to emp centers)
> fit_d3 <- lm(nox ~ poly(dis, 3, raw=TRUE), data=Boston)
> summary(fit_d3)

Call:
lm(formula = nox ~ poly(dis, 3, raw = TRUE), data = Boston)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.121130 -0.040619 -0.009738  0.023385  0.194904 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept)                0.9341281  0.0207076  45.110  < 2e-16 ***
poly(dis, 3, raw = TRUE)1 -0.1820817  0.0146973 -12.389  < 2e-16 ***
poly(dis, 3, raw = TRUE)2  0.0219277  0.0029329   7.476 3.43e-13 ***
poly(dis, 3, raw = TRUE)3 -0.0008850  0.0001727  -5.124 4.27e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.06207 on 502 degrees of freedom
Multiple R-squared:  0.7148,    Adjusted R-squared:  0.7131 
F-statistic: 419.3 on 3 and 502 DF,  p-value: < 2.2e-16

> coef(summary(fit_d3))
                               Estimate   Std. Error    t value      Pr(>|t|)
(Intercept)                0.9341280720 0.0207076150  45.110365 9.853624e-179
poly(dis, 3, raw = TRUE)1 -0.1820816950 0.0146973264 -12.388763  6.078843e-31
poly(dis, 3, raw = TRUE)2  0.0219276580 0.0029329119   7.476412  3.428917e-13
poly(dis, 3, raw = TRUE)3 -0.0008849957 0.0001727172  -5.123959  4.274950e-07
> plot(Boston$dis, Boston$nox)
> lines(sort(Boston$dis), fit_d3$fitted.values[order(Boston$dis)], col = 2, lwd = 3)