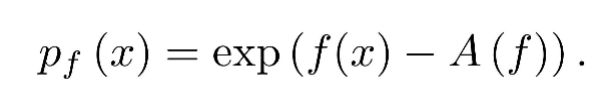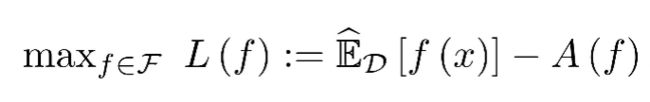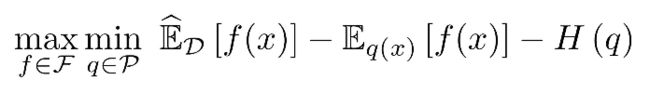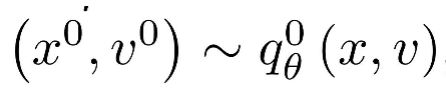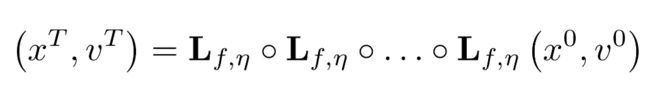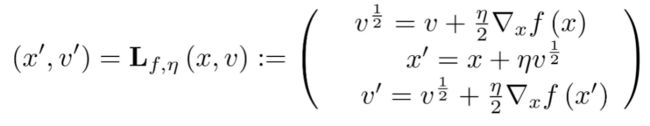蚂蚁金服：如何训练可自动调整负样本采样器？｜NIPS 2019
作者 | 蚂蚁金服
编辑 | Jane
出品 | AI科技大本营（ID：rgznai100）
【导读】一年一度的国际顶级学术会议NeurIPS2019将于12月8日至14日在加拿大温哥华举行。作为人工智能和机器学习领域最顶级的盛会之一，NeurIPS每年都会吸引来自全世界的AI大牛、学者、技术爱好者参会。本文是蚂蚁金服的技术专家对入选论文《使用对抗式动态系统嵌入的深度指数族分布估计》做出的深度解读。
前言
指数分布族 （exponential family），同时又被称为能量模型（energy-based model），是一类广泛应用的生成式概率模型。通过和深度模型结合，指数分布族能够灵活的拟合各种数据分布。由于指数分布族的灵活性，目前已经有越来越多的研究者利用指数分布族对各种结构数据进行建模。例如，[1] 将能量模型用于对蛋白质结构预测，从而更好的指导药物设计和材料科学；[2] 将能量模型用于语言模型及句子生成；[3] 将能量模型用于基于模型的强化学习；等等。这些都展示了指数族分布能量模型作为有别于变分自编码器（variational autoencoder）和对抗式生成模型（generative adversarial network）之外，另一种截然不同的生成式模型的能力和潜在应用。但是，如何有效的求解通用指数分布族的最大似然估计（MLE）以及如何高效的进行推断仍然是一个亟待解决的问题。
摘要
针对通用深度指数分布族有效求解最大似然估计这一问题，我们利用最大似然的primal-dual reformulation，将原始MLE中不可解的log-partition 函数重写成能量函数（potential function）针对对一个可学习的负样本采样器（negative sampler）的期望。通过这样的形式，我们可以同时学习能量函数以及负样本采样器。相比现存的方法，使用手工设计的固定的，我们的算法可以根据训练样本自动调整负样本采样器，以便更好的学习模型。与此同时，学习得到的负样本采样器可以用来平摊统计推断（amortized inference）。
基于这样的框架，我们进一步模仿哈密尔动态系统顿蒙特卡洛采样器（Hamiltonian Monte-Carlo （HMC）），并加入可学习模块来设计HMC负样本神经网络采样器。这样的采样器有一下两个优点：
1. 可以使得负样本神经网络采样器也采用了能量函数中的参数；
2. 设计得到的HMC负样本神经网络采样器有可计算的熵函数表示，从而可以带入到我们的primal-dual form of MLE中。
这一框架同时将现存的各种能量模型学习算法统一在一个清晰的观点下。我们严格证明了对照散度（contrasitive divergence），伪最大似然（pseudo/composite-likelihood）, 分数匹配（score matching）, 最小化Stein差异（minimum Stein discrepancy estimator）, 非局部对照目标（non-local contrastive objectives）, 噪声对照估计（noise-contrastive estimation）, 以及最小化概率流（ minimum probability flow）等等能量模型估计方法都是我们框架下的特例：在学习中使用了某种手工设计的固定负样本采样器。
对抗式动态系统嵌入（Adversarial Dynamics Embedding ）简介
1、最大似然的 Primal-Dual 表示
深度指数分布族（能量模型）表示为
其中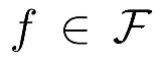
为神经网络，叫做能量函数；而 
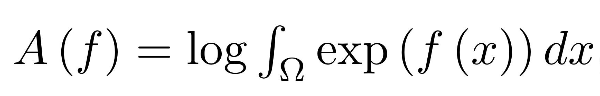叫做log-partition function。使用这样的符号，能量模型的MLE可以写成：
注意到log-partition function 不可计算，直接求解MLE非常困难。我们利用Fenchel 对偶函数，我们可以将MLE重新写成
引入学习负样本采样器q(x)，从而避免到直接计算log-partition function。
2、动态系统采样器设计
在MLE的primal-dual 表示中，我们引入负样本采样器避免不可计算的部分。学习到的potential function的实际表现依赖于负样本采样的灵活性。于此同时，primal-dual 表示也要求负样本的熵可计算。我们知道动态系统采样器HMC可以近似任意的能量模型，而且HMC的argumented 熵是可计算的。因此，我们推广了HMC采样器，将每个HMC step当作一个cell来组成神经网络。
具体来说，当初始
，我们设计T层HMC神经网络为
其中
同理，我们可以设计Langevin神经网络以及广义HMC神经网络。这样的负样本采样器
将这样的负样本采样器带入MLE的primal-dual 形式，我们得到了最终的优化目标：
这样以来，我们可以使用随即梯度优化（stochastic gradient descent）来对目标函数进行优化。其中f 是原始potential function，
表示负样本采样器中的参数，包括初始分布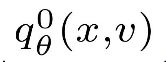
中的参数，以及HMC step cell 中的参数
。
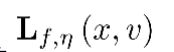实验结果
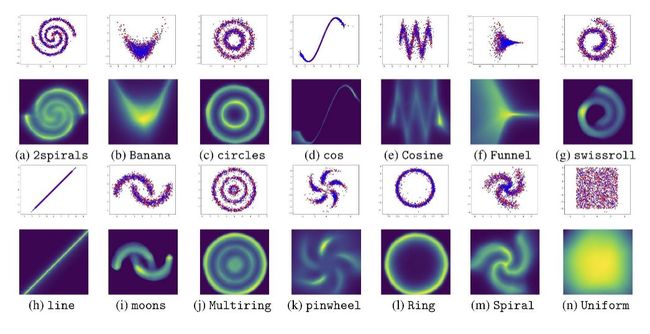
上图展示了我们提出的ADE算法在synthetic 数据上的结果。其中奇数列展示学到的negative sampler：其中红色样本点是训练数据，蓝色是学习到的采样器生成的样本。可以看到我们学习到的采样器能够很好的复原训练数据分布。图中的偶数列表示学习到的potential function。可以看到通过ADE学习到的potential function 符合训练数据中密度高的地方。
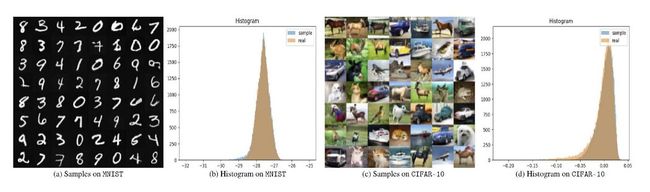
我们将ADE应用到训练real-world image上的深度能量模型并在MNIST和CIFAR-10进行测试。图1和图3展示了从学习到的采样器中抽样得到的样本。可以看到学习到的采样器能够生成非常逼真的图像样本。图2和图4展示了学习得到potential function在训练数据（橙色）以及生成数据（蓝色）上的直方图对比。学习得到的potential function 在生成数据和训练数据上匹配的非常好。
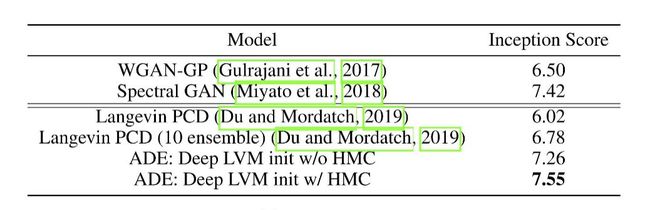
我们还提供了数量性质的比较。因为我们学习到的采样器可以用来生成图片，我们和已有的生成模型进行了比较，包括WGAN-GP，Spectral-GAN，以及使用固定Langevin sampler 作为负样本采样器学习得到的能量模型。ADE得到的模型能够在Inception Score下生成更好的样本。除此之外，我们还验证了learnable HMC的效果。相比ADE without HMC，在ADE中使用数据自动调整过的HMC能够提升IS。
[1] Ingraham, John, Adam Riesselman, Chris Sander, and Debora Marks. "Learning protein structure with a differentiable simulator." (2018).
[2] Du, Yilun, Toru Lin, and Igor Mordatch. "Model based planning with energy based models." arXiv preprint arXiv:1909.06878 (2019).
[3] Bakhtin, Anton, Sam Gross, Myle Ott, Yuntian Deng, Marc'Aurelio Ranzato, and Arthur Szlam. "Real or Fake? Learning to Discriminate Machine from Human Generated Text." arXiv preprint arXiv:1906.03351 (2019).
（*本文为AI科技大本营投稿文章，转载请微信联系 1092722531）
◆
精彩公开课
◆
推荐阅读
大四学生发明文言文编程语言，设计思路清奇
芬兰开放“线上AI速成班”课程，全球网民均可免费观看
超模脸、网红脸、萌娃脸...换头像不重样？我开源了5款人脸生成器
解读 | 2019年10篇计算机视觉精选论文（上）
高通：2 亿像素手机 2020 年诞生！
英特尔首推异构编程神器 oneAPI，可让程序员少加班！
VS Code 成主宰、Vue 备受热捧！2019 前端开发趋势必读
我在华为做外包的真实经历
2019 区块链大事记 | Libra 横空出世，莱特币减产，美国放行 Bakkt……这一年太精彩！
互联网诞生记: 浪成于微澜之间
你点的每个“在看”，我都认真当成了AI