一元线性回归及非线性回归(学习笔记)
回归(Regression)
”回归到中等“
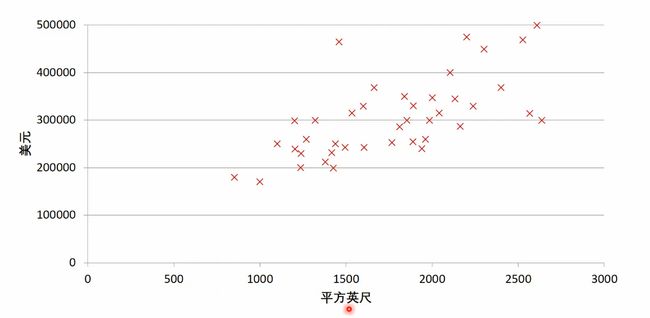
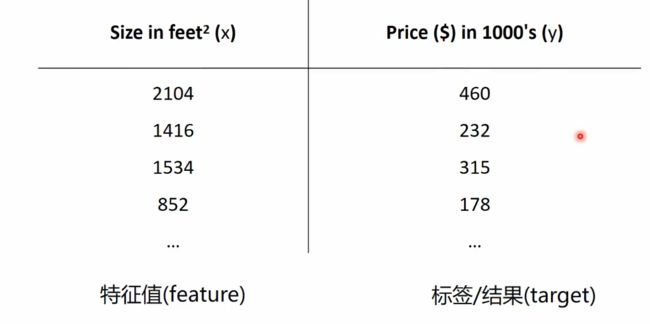
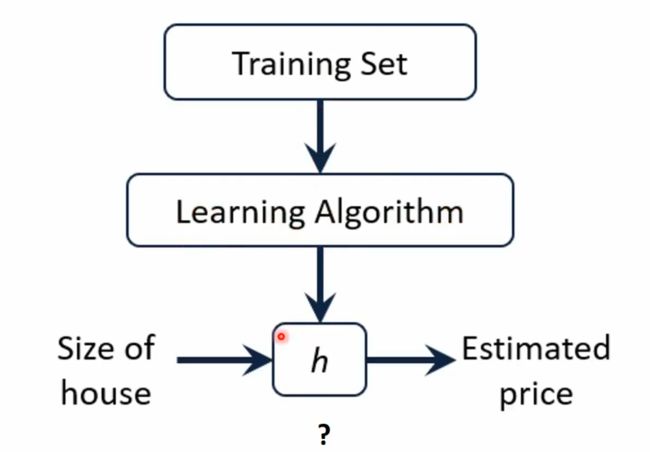
房价预测:- 回归分析(regression analysis)用来建立方程模拟两个或者多个变量之间如何关联
- 被预测的变量叫做:因变量(dependent variable),输出(output)
- 被用来进行预测的变量叫做:自变量(independent variable),输入(input)
- 一元线性回归包含一个自变量和一个因变量
- 以上两个变量的关系用一条直线来模拟
- 如果包含两个以上的自变量,则称作多元回归分析(multiple regression)
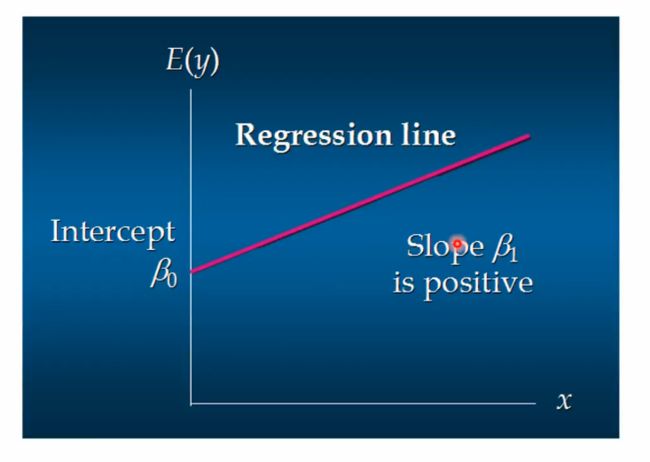
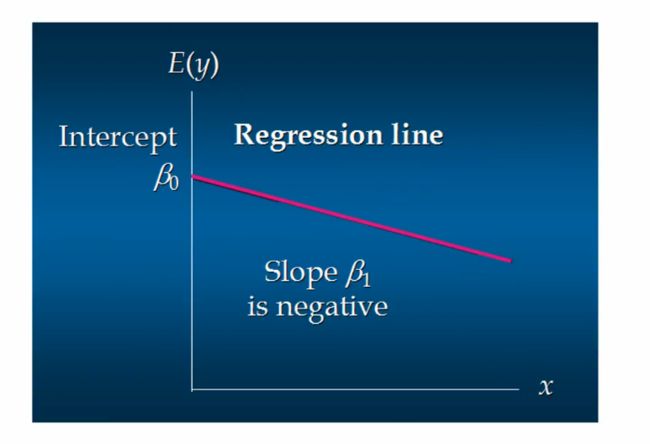
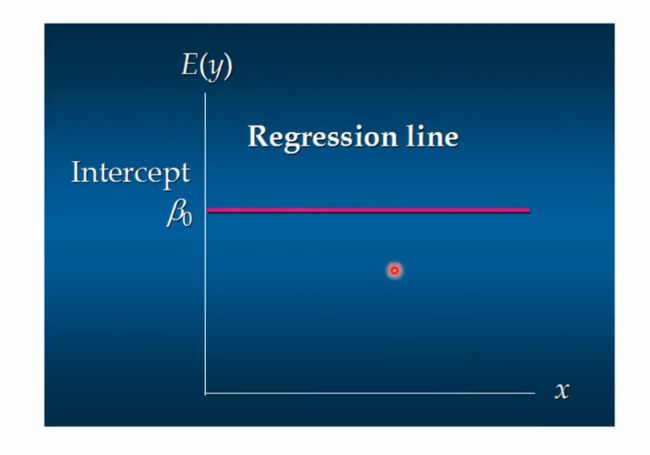
a θ ( x ) = θ 0 + θ 1 x a_\theta(x) = \theta_0 + \theta_1x aθ(x)=θ0+θ1x
这个方程对应的图像是一条直线,称作回归线。其中, θ 1 \theta_1 θ1为回归线的斜率, θ 0 \theta_0 θ0为回归线的截距. x x x是因为只有一个自变量。
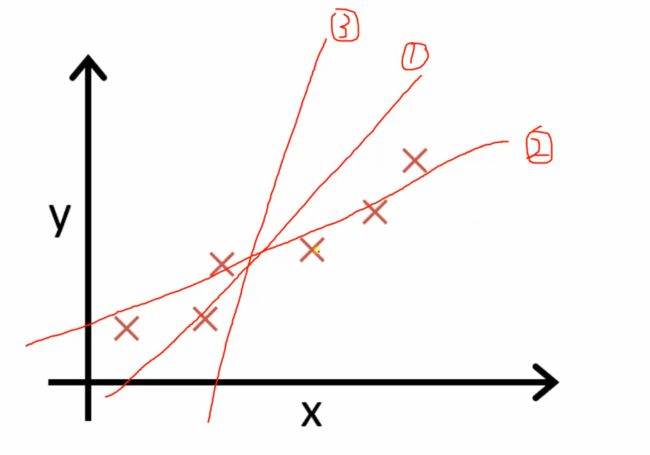
求解方程系数:
判断哪一条线最好:
代价函数(Cost Function)
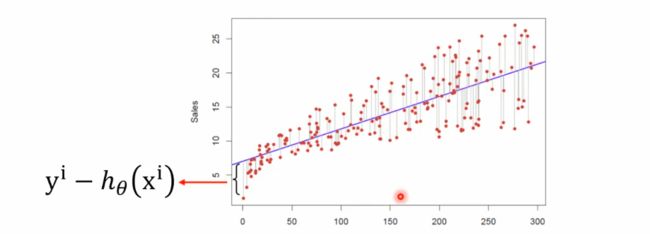
- 最小二乘法
- 真实值y,预测值 h θ ( x ) h_\theta(x) hθ(x),则误差平方为 ( y − h θ ( x ) ) 2 (y -h_\theta(x))^2 (y−hθ(x))2
- 找到核视的参数,使的误差平方和:
j ( θ 0 , θ 1 ) = 1 2 m ∑ ( i = 1 ) m ( y i − h θ ( x i ) ) 2 最 小 j(\theta_0,\theta_1) = \frac{1}{2m}\sum_(i = 1)^m(y^i - h_\theta(x^i))^2 最小 j(θ0,θ1)=2m1(∑i=1)m(yi−hθ(xi))2最小
假设的目标一元线性回归方程:
a θ ( x ) = θ 0 + θ 1 x a_\theta(x) = \theta_0 + \theta_1x aθ(x)=θ0+θ1x
该方程的参数有两个分别为:
θ 0 , θ 1 \theta_0,\theta_1 θ0,θ1
该方程的代价函数为:
j ( θ 0 , θ 1 ) = 1 2 m ( ∑ i = 0 m ( y i − h θ ( x i ) ) 2 j(\theta_0,\theta_1) = \frac{1}{2m}(\sum_{i=0}^m(y^i - h_\theta(x^i))^2 j(θ0,θ1)=2m1(i=0∑m(yi−hθ(xi))2
预期的目标是:
a r g m i n j ( θ 0 , θ 1 ) arg~min~j(\theta_0,\theta_1) arg min j(θ0,θ1)
即
a r g m i n ( θ 0 , θ 1 ) 1 2 m ( ∑ i = 0 m ( y i − h θ ( x i ) ) 2 arg~min_{(\theta_0,\theta_1)}~~\frac{1}{2m}(\sum_{i=0}^m(y^i - h_\theta(x^i))^2 arg min(θ0,θ1) 2m1(i=0∑m(yi−hθ(xi))2
为了研究简化以上步骤,先只对 θ 1 \theta_1 θ1进行研究,截距 θ 0 = 0 \theta_0 = 0 θ0=0
得到的方程如下:
a θ ( x ) = θ 1 x a_\theta(x) = \theta_1x aθ(x)=θ1x
该方程的代价函数为:
j ( θ 1 ) = 1 2 m ( ∑ i = 0 m ( y i − h θ ( x i ) ) 2 j(\theta_1) = \frac{1}{2m}(\sum_{i=0}^m(y^i - h_\theta(x^i))^2 j(θ1)=2m1(i=0∑m(yi−hθ(xi))2
预期目标变为:
a r g m i n j ( θ 1 ) a r g m i n ( θ 1 ) 1 2 m ( ∑ i = 0 m ( y i − h θ ( x i ) ) 2 arg~min~j(\theta_1) arg~min_{(\theta_1)}~~\frac{1}{2m}(\sum_{i=0}^m(y^i - h_\theta(x^i))^2 arg min j(θ1)arg min(θ1) 2m1(i=0∑m(yi−hθ(xi))2
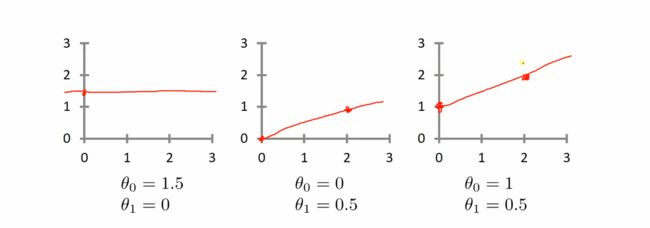
举例:这里令 θ 0 = 0 \theta_0 = 0 θ0=0,改变 θ 1 \theta_1 θ1的值,观察costFunction的变化情况:
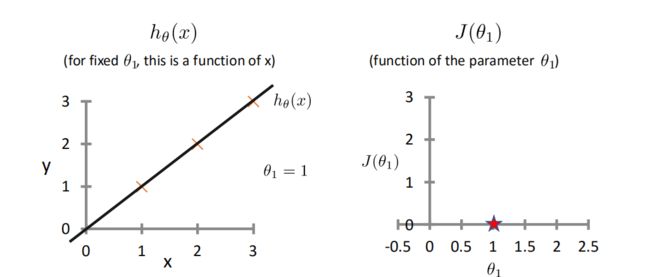
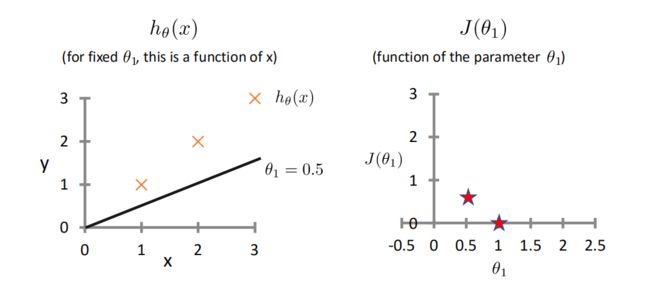
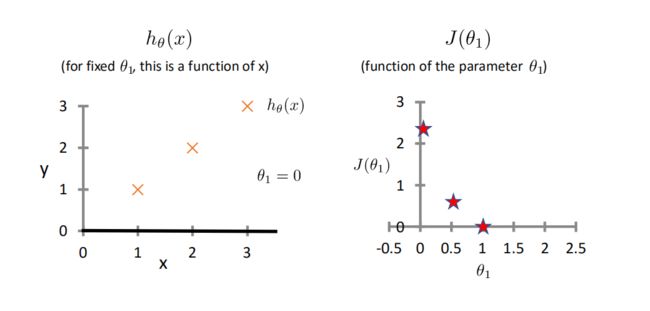
将大量 θ 1 \theta_1 θ1带入运算,最终得到关于 θ 1 \theta_1 θ1的costfunction的图像:
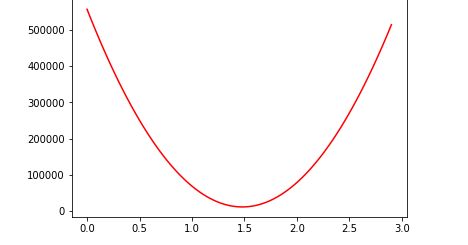
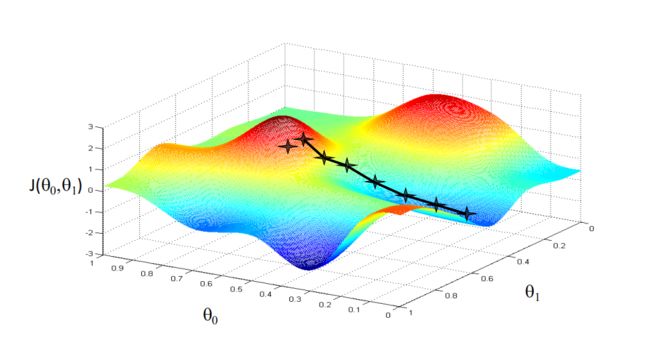
而若同时考虑 θ 0 \theta_0 θ0与 θ 1 \theta_1 θ1时,图像如下:
这便是代价函数(cost function)
代价函数其实也是均方误差,而均方误差有非常好的几何意义,它对应了常用的欧几里得距离或简称“欧氏距离”(Euclidean distance)。基于均方误差最小化来进行模型求解的方法称为“最小二乘法”(least square method),在线性回归中,最小二乘法就是试图找到一条直线,使所有样本到直线上的欧式距离最小。
梯度下降法(Gradient Descent)
当我们有了一个代价函数 j ( θ 0 , θ 1 ) j(\theta_0,\theta_1) j(θ0,θ1)后,如何去寻找 m i n ( θ 0 , θ 1 ) j ( θ 0 , θ 1 ) min_{(\theta_0,\theta_1)}j(\theta_0,\theta_1) min(θ0,θ1)j(θ0,θ1)呢?
我们需要:
- 初始化 θ 0 , θ 1 \theta_0,\theta_1 θ0,θ1
- 不断改变 θ 0 , θ 1 \theta_0,\theta_1 θ0,θ1,直到 j ( θ 0 , θ 1 ) j(\theta_0,\theta_1) j(θ0,θ1)达到一个全局最小值,或者局部极小值。(不断迭代,优化函数模型)
此时我们便需要梯度下降函数来帮助我们寻找极小值(最小值)
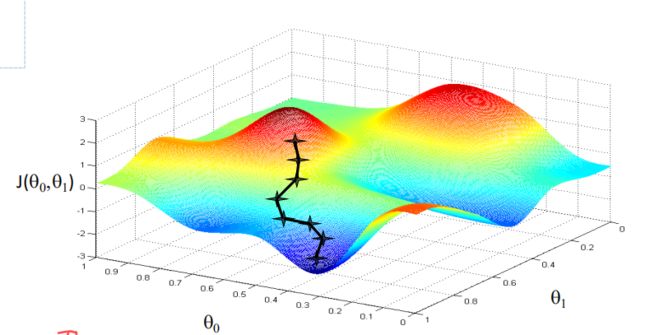
在图像上任取一点,在对这个点求导,这个导数,便是这个点的梯度,我们沿着这个梯度不断下降,便可以成功的到达最低点,也就是 a r g m i n j ( θ 0 , θ 1 ) arg~min~j(\theta_0,\theta_1) arg min j(θ0,θ1)。当然如果我们初始点选的位置不好,那便会下降到局部的极小值点处,而非全局最小值点。如图:
这个迭代方法,称为梯度下降法,用函数表示成:
梯度下降函数(gradient-decent)
r e p e a t u n t i l c o n v e r g e n c e θ j = θ j − α ∂ ∂ θ j ( f o r j = 0 a n d j = 1 ) repeat~until~convergence\\ \theta_j = \theta_j - \alpha\frac{\partial}{\partial\theta_j}(for~j = 0~and~j = 1) repeat until convergenceθj=θj−α∂θj∂(for j=0 and j=1)
其中 α \alpha α称为学习率(learning rate)
注:
在对 j ( θ 0 , θ 1 ) j(\theta_0,\theta_1) j(θ0,θ1)更新时,我们需要的是同步更新,即:
t e m p 0 : = θ 0 − α ∂ ∂ θ 0 j ( θ 0 , θ 1 ) t e m p 1 : = θ 1 − α ∂ ∂ θ 1 j ( θ 0 , θ 1 ) θ 0 : = t e m p 0 θ 1 : = t e m p 1 temp0 := \theta_0 - \alpha\frac{\partial}{\partial\theta_0}j(\theta_0,\theta_1)\\ temp1 := \theta_1 - \alpha\frac{\partial}{\partial\theta_1}j(\theta_0,\theta_1)\\ \theta_0 :=temp0\\ \theta_1 :=temp1\\ temp0:=θ0−α∂θ0∂j(θ0,θ1)temp1:=θ1−α∂θ1∂j(θ0,θ1)θ0:=temp0θ1:=temp1
而不是以下这种异步更新:
t e m p 0 : = θ 0 − α ∂ ∂ θ 0 j ( θ 0 , θ 1 ) θ 0 : = t e m p 0 t e m p 1 : = θ 1 − α ∂ ∂ θ 1 j ( θ 0 , θ 1 ) θ 1 : = t e m p 1 temp0 := \theta_0 - \alpha\frac{\partial}{\partial\theta_0}j(\theta_0,\theta_1)\\ \theta_0 :=temp0\\ temp1 := \theta_1 - \alpha\frac{\partial}{\partial\theta_1}j(\theta_0,\theta_1)\\ \theta_1 :=temp1\\ temp0:=θ0−α∂θ0∂j(θ0,θ1)θ0:=temp0temp1:=θ1−α∂θ1∂j(θ0,θ1)θ1:=temp1
这种方法有可能会得到正确的答案,但异步更新并不是梯度下降函数所定义的跟新方法。
学习率
关于学习率,它是用来调节每次函数梯度下降时,下降的高度。用图说话:
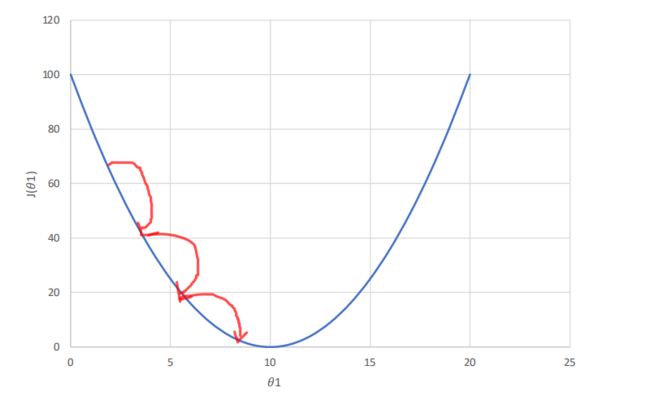
下图是关于 θ 1 \theta_1 θ1的costfunction
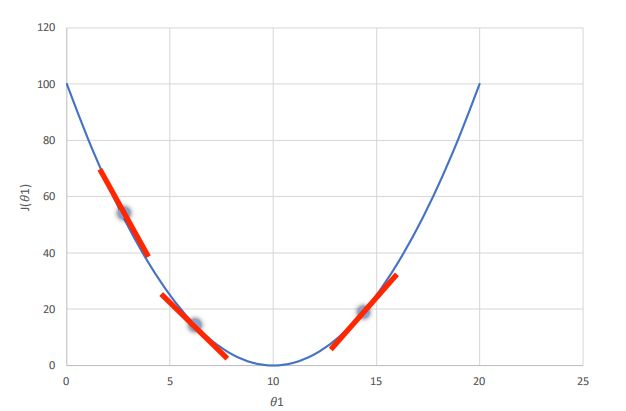
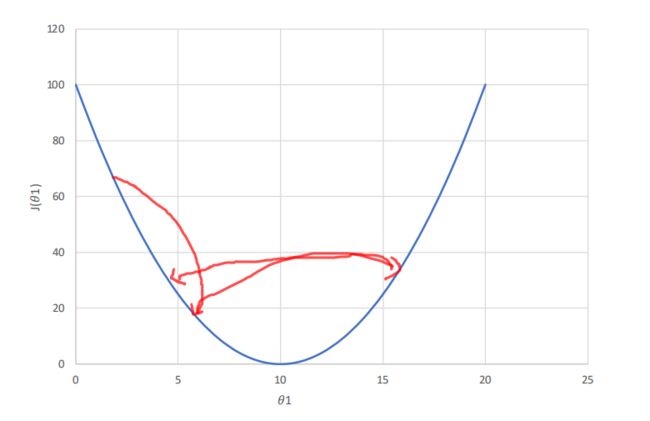
但是学习率也不能设置过小,设置过小,会导致函数迭代次数过多,消耗大量资源,时间消耗较大:
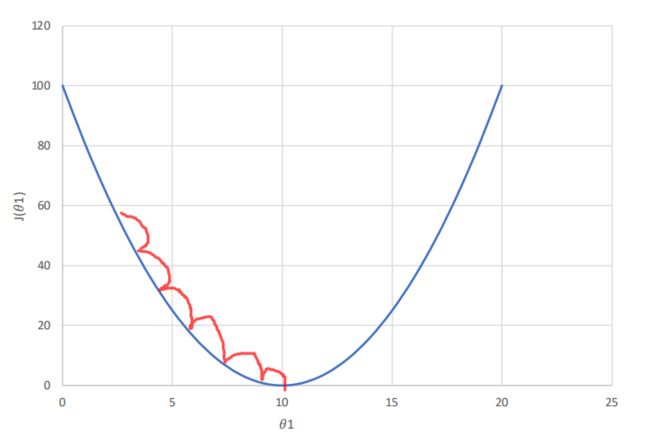
梯度下降法的缺点也很明显,不同的起点选择,有可能会下降到局部极小值,而不能正确的取到全局最小值,如图:
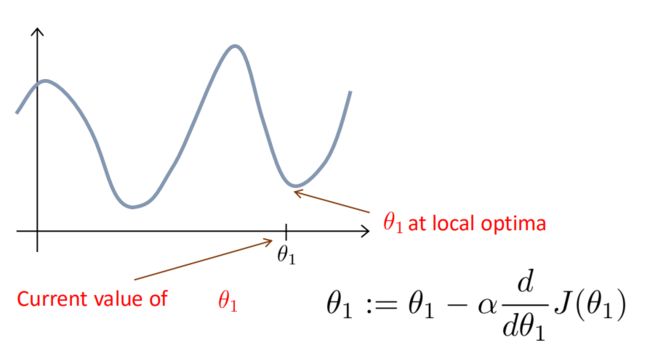
可见学习率不能太小,也不能太大,可以多尝试一些值(0.1.0.001,0.003,0.002,。。。)
用梯度下降法来求解线性回归
梯度下降法:
r e p e a t u n t i l c o n v e r g e n c e θ j = θ j − α ∂ ∂ θ j ( f o r j = 0 a n d j = 1 ) repeat~until~convergence\\ \theta_j = \theta_j - \alpha\frac{\partial}{\partial\theta_j}(for~j = 0~and~j = 1) repeat until convergenceθj=θj−α∂θj∂(for j=0 and j=1)
线性回归的模型和代价函数:
a θ ( x ) = θ 0 + θ 1 x j ( θ 0 , θ 1 ) = 1 2 m ( ∑ i = 0 m ( y i − h θ ( x i ) ) 2 a_\theta(x) = \theta_0 + \theta_1x \\ j(\theta_0,\theta_1) = \frac{1}{2m}(\sum_{i=0}^m(y^i - h_\theta(x^i))^2 aθ(x)=θ0+θ1xj(θ0,θ1)=2m1(i=0∑m(yi−hθ(xi))2
对上式分别求偏导得:
r e p e a t u n t i l c o n v e r g e n c e θ 0 = θ 0 − α 1 m ( ∑ i = 0 m ( y i − h θ ( x i ) ) θ 1 = θ 1 − α 1 m ( ∑ i = 0 m ( y i − h θ ( x i ) ) ⋅ x ( i ) repeat~until~convergence \\ \theta_0 = \theta_0 - \alpha\frac{1}{m}(\sum_{i=0}^m(y^i - h_\theta(x^i)) \\ \theta_1 = \theta_1 - \alpha\frac{1}{m}(\sum_{i=0}^m(y^i - h_\theta(x^i)) · x^{(i)} repeat until convergenceθ0=θ0−αm1(i=0∑m(yi−hθ(xi))θ1=θ1−αm1(i=0∑m(yi−hθ(xi))⋅x(i)
用以上方法,便可对简单的线性模型进行线性回归
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#载入数据
data = pd.read_csv("data.csv",encoding="gbk",header=None)
#数据切割
x_data = data.iloc[:,0]
y_data = data.iloc[:,1]
#设置图像大小
plt.xlim(20,80)
plt.ylim(20,120)
#显示散点图
plt.scatter(x_data,y_data,c = 'r')
plt.show()
#设置学习率
lr = 0.0001
#截距theta1
theta1 = 0
#斜率theta0
theta0 = 0
#样本总个数
m = len(x_data)
#最大迭代次数
epochs = 50
#代价函数
def CostFunction(theta0, theta1, x_data, y_data, m):
totalError = 0
for i in range(m):
totalError += ((theta0 + theta1 * x_data[i]) - y_data[i])**2
return totalError / float(( 2 * m))
a = np.ones(50)
b = np.ones(50)
ans = np.ones(50)
#梯度下降函数
def gradient_decent(theta0, theta1, lr, m, x_data, y_data , epochs):
for i in range(epochs):
theta0_grad = 0
theta1_grad = 0
for j in range(m):
theta0_grad += (theta0 + theta1 * x_data[j]) - y_data[j]
theta1_grad += ((theta0 + theta1 * x_data[j]) - y_data[j]) * x_data[j]
theta0 = theta0 - lr * (1 / m) * theta0_grad
theta1 = theta1 - lr * (1 / m) * theta1_grad
a[i] = theta0;
b[i] = theta1;
ans[i] = CostFunction(theta0,theta1,x_data,y_data,m)
##每迭代5次,输出一次图像
#if i % 5 == 0:
# print("epochs:",i)
# plt.plot(x_data,y_data,'b.')
# plt.plot(x_data,theta1 * x_data + theta0,'r')
# plt.show()
return theta0,theta1
theta0,theta1 = gradient_decent(theta0, theta1, lr, m, x_data, y_data , epochs)
plt.scatter(x_data,y_data,c = 'r')
plt.plot(x_data,theta0 + theta1 * x_data,'b')
plt.show()
print(theta0,theta1,CostFunction(theta0,theta1,x_data ,y_data , m))
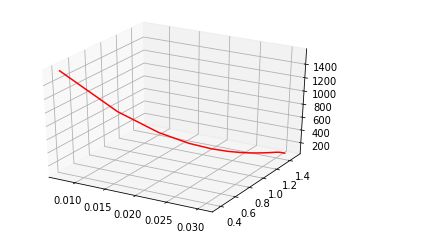
#3D梯度下降
ax = plt.axes(projection='3d')
ax.plot3D(a,b,ans,'red')
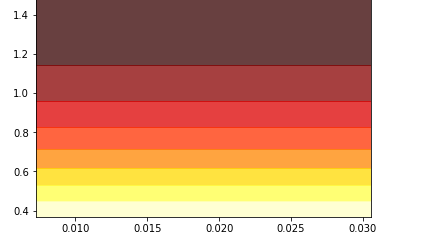
#3d等高线梯度下降
A,B = np.meshgrid(a,b)
ans = CostFunction(A,B,x_data,y_data,m)
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(A,B,ans,rstride = 1,cstride = 1,cmap = plt.get_cmap('rainbow'))
#2d等高线
plt.contourf(A,B,ans,7,alpha = 0.75,cmap = plt.cm.hot)
plt.show()
凸函数(convex)
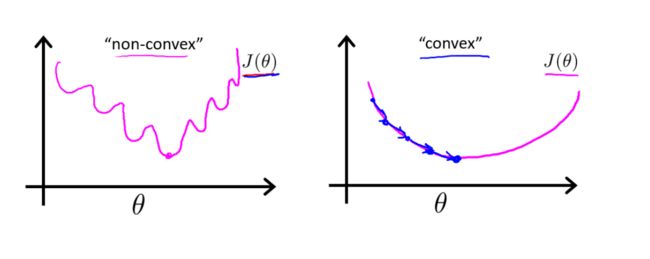
在处理线性回归问题时,若采用梯度下降的方法,我们理想的代价函数函数便是上图右侧的凸函数(convex),而左侧的非凸函数(non-convex)很容易取到局部极小值,对线性回归有很大的干扰,往往得不到正确的结果。