上一节我们实现了编译原理中语法解析入门,能够解析简单的由let关键字开头的变量定义语句,现在我们再接再厉,实现解析由return 开头的返回值语句。由于return 后面可以跟着一个变量,一个数值,一个函数调用,以及一个带有操作符的计算式,这几种情况,我们统一用算术表达式来归纳。因此对应于return 语句的语法解析表达式是:
ReturnStatement := return Expression
为了简单起见,我们代码实现时,任然假设return 后面跟着一个数字字符串,后面我们会深入探讨如何解析异常复杂的算术表达式。在MonkeyCompilerParser.js中添加如下代码:
parseStatement() {
switch (this.curToken.getType()) {
case this.lexer.LET:
return this.parseLetStatement()
//change here
case this.lexer.RETURN:
return this.parseReturnStatement()
...
}
}
上面代码表明,如果解析器读取token 序列时,如果遇到关键字return,那么就调用parseReturnStatement来解析接下来的代码,我们看看它的实现:
parseReturnStatement() {
var props = {}
props.token = this.curToken
//change later
if (!this.expectPeek(this.lexer.INTEGER)) {
return null
}
var exprProps = {}
exprProps.token = this.curToken;
props.expression = new Expression(exprProps)
if (!this.expectPeek(this.lexer.SEMICOLON)) {
return null
}
return new ReturnStatement(props)
}
在上面代码的实现中,它检测跟着return关键字后面的是否是数字字符串,如果不是,那表示语法出错,如果是,那么再判断数字后面是否以分号结尾,如果这些条件都满足的话,那表明当前解析到的代码语句确实符合return语句的语法规定,于是就构建一个ReturnStatement对象返回,该对象与我们上一节实现的LetStatement类几乎一致,代码如下:
class ReturnStatement extends Statement{
constructor(props) {
super(props)
this.token = props.token
this.expression = props.expression
var s = "return with " + this.expression.getLiteral()
this.tokenLiteral = s
}
}
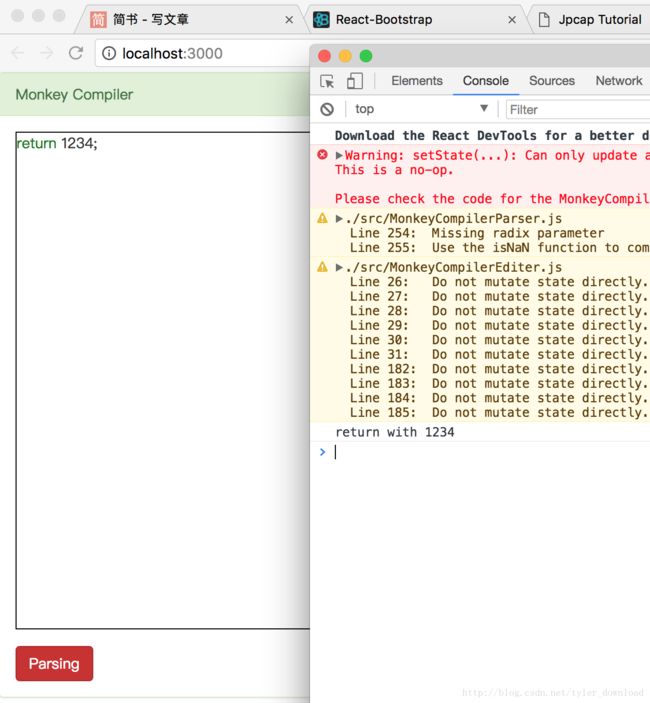
上面代码完成后,我们在编辑框输入return 语句,点击下面红色的解析按钮后,结果如下:
可以看到,点击按钮后,在控制台上显示了“return with 1234"的语句,这表明我们的语法解析器能够识别return语句。接下来我们进入到复杂算术表达式的解析阶段,这里是编译原理算法的一大难点所在。
算术表达式的解析之所以困难,主要在于表达式类型多样,并且需要考虑运算符的优先级,例如 5 * 5 + 10 , 语法解析器就得明白,需要先做乘法,然后再做加法,因为乘法的优先级要高于加法。对于算术表达式:(5+5)*10,则要先做加法,再做乘法,因为括号的优先级要高于乘号。
解析器还得考虑不同操作符产生不同含义的表达式,例如 -5 表示的是一个数值也就是负五,而--5 表示的是一次算术操作,意思是计算5-1所得的值,也就是4.
同时,解析器还得考虑符号的次序,操作符在操作数的前面则称为前序操作符,例如-5, --5, !true 等,这些运算符都叫前序操作符;5-1, 2*3 这些表达式的符号夹在两个操作数中间,所以叫中序操作符;而5--, 5++ 这些表达式中,符号在操作数的后面,因此叫后续操作符。
此外,表达式还可以是异常复杂的形式表现,例如:5 * add(5,6) + 3, add(add(5,3), add(6,7)), 前面表达式在运算中包含函数调用,后面表达式是函数调用中又包含着函数调用,由于算术表达式展现形式多种多样,要通过它光怪陆离的表象识别它的本质是一件很困难的事情,因此,语法解析器对算术表达式解析算法的发明和实现是计算机科学发展史上光辉的一页。
计算机科学家,斯坦福大学教授,梵高.普拉特(Vaughan Pratt)发明了一种非常聪明且优雅的解析算法,但一直不被学界所认识,后来由大牛Douglas Crockford,也就是写了“JavaScript: The Good Parts" 这本书的作者大力举荐,并通过展示该算法能快速有效的解析javascript语法。同时依靠该算法开发出了JS语言的静态检测器JSLint后,该算法才被业界所熟知。我们这里就采用Pratt发明的算法,名为“自顶向下的操作符优先级解析法”来解析Monkey语言的算术表达式,以下是该算法的描述链接,大家可以点击阅读:
http://crockford.com/javascript/tdop/tdop.html
道可道,非常道。有些原理是很难通过语言描述出来的,对他的理解,你只能去感知,而不能简单的去阅读,编译原理就属于这类型理论,在大学里,编译原理之所以被大家视若危途,就是因为理论讲起来晦涩难懂,其实只要有代码让学生亲手尝试一下,要掌握理论其实根本不难,我们采用的就是第二种办法,通过代码的编写和调试来讲解理论,而不是用嘴巴说话来讲解理论,抽象的原理就像“爱”,说没用,做才有用!
我们现在代码中增加一个类,用来表示算术表达式:
class ExpressionStatement extends Statement {
constructor(props) {
super(props)
this.token = props.token
this.expression = props.expression
var s = "expression: " + this.expression.getLiteral()
this.tokenLiteral = s
}
}
代码原来跟以前的LetStatement, ReturnStatement一样,没有独特之处。接下来我们设计一个解析函数表,当解析器遇到某种类型的token时,它就根据token在表里拿出一个解析函数,执行这个函数就能实现对当前token的解析,因此代码如下:
class MonkeyCompilerParser {
constructor(lexer) {
....
//change here
this.LOWEST = 0
this.EQUALS = 1 // ==
this.LESSGREATER = 2 // < or >
this.SUM = 3
this.PRODUCT = 4
this.PREFIX = 5 //-X or !X
this.CALL = 6 //myFunction(X)
this.prefixParseFns = {}
this.prefixParseFns[this.lexer.IDENTIFIER] =
this.parseIdentifier
this.prefixParseFns[this.lexer.INTEGER] =
this.parseIntegerLiteral
}
}
我们提到的函数表就是prefixParseFns, 从代码可以看成,如果解析器当前遇到的token类型是变量字符串,也就是lexer.IDENTIFIER,时,解析器就从该表中拿出parseIdentifier这个函数来执行,如果解析器当前遇到的token类型是数组字符串,那么它便从该表中拿出函数parseIntegerLiteral来执行。于是我们的解析主函数及上面函数表中对应的两个函数实现如下:
parseStatement() {
switch (this.curToken.getType()) {
case this.lexer.LET:
return this.parseLetStatement()
//change here
case this.lexer.RETURN:
return this.parseReturnStatement()
default:
//change here
return this.parseExpressionStatement()
}
}
....
//change here
parseExpressionStatement() {
var props = {}
props.token = this.curToken
props.expression = this.parseExpression(this.LOWEST)
var stmt = new ExpressionStatement(props)
if (this.peekTokenIs(this.lexer.SEMICOLON)) {
this.nextToken()
}
return stmt
}
createIdentifier() {
var identProps = {}
identProps.token = this.curToken
identProps.value = this.curToken.getLiteral()
return new Identifier(identProps)
}
//change here
parseExpression(precedence) {
var prefix = this.prefixParseFns[this.curToken.getType()]
if (prefix === null) {
return null
}
return prefix(this)
}
//change here
parseIdentifier(caller) {
return caller.createIdentifier()
}
//change here
parseIntegerLiteral(caller) {
var intProps = {}
intProps.token = caller.curToken
intProps.value = parseInt(caller.curToken.getLiteral())
if (intProps.value === NaN) {
console.log("could not parse token as integer")
return null
}
return new IntegerLiteral(intProps)
}
在函数parseStatement中,如果解析器当前遇到的token不是关键字let 或者return,那么他就调用parseExpressionStatement来进行算术表达式的解析。在该函数里,它调用parseExpression来做解析,在后者的实现中,它就是非常简单的拿着当前token到函数表里去查询,拿到对应的解析函数后直接执行就可以了,调用这个函数时传入了一个参数叫precedence,它是用来表示解析优先级的,这点我们在后面再进行探讨。
如果当前对应的token是变量字符串,也就是IDENTIFIER,那么函数parseIdentifier就会被调用,它直接调用createIdentifier,后者则是用当前token构建一个Identifier类的实例即可。如果当前解析器读取到的是数字字符串,那么它会从表中找到函数parseIntegerLiteral来执行,该函数根据当前token,把它的内容解析成整形数值后,创建一个IntegerLiteral的类实例。IntegerLiteral的定义如下:
class IntegerLiteral extends Expression {
constructor(props) {
super(props)
this.token = props.token
this.value = props.value
var s = "Integer value is: " + this.token.getLiteral()
this.tokenLiteral = s
}
}
上面的代码完成后,解析器就可以解析算术表达式的两种特殊情况,也就是变量和数字。从这里我们可以看到,Pratt解析法的精髓就是通过建立一张表,把不同类型token的解析对应到不同的函数,解析器只需机械的根据当前token对象查表并执行就可以了,于是解析器的设计逻辑得以大大简化。
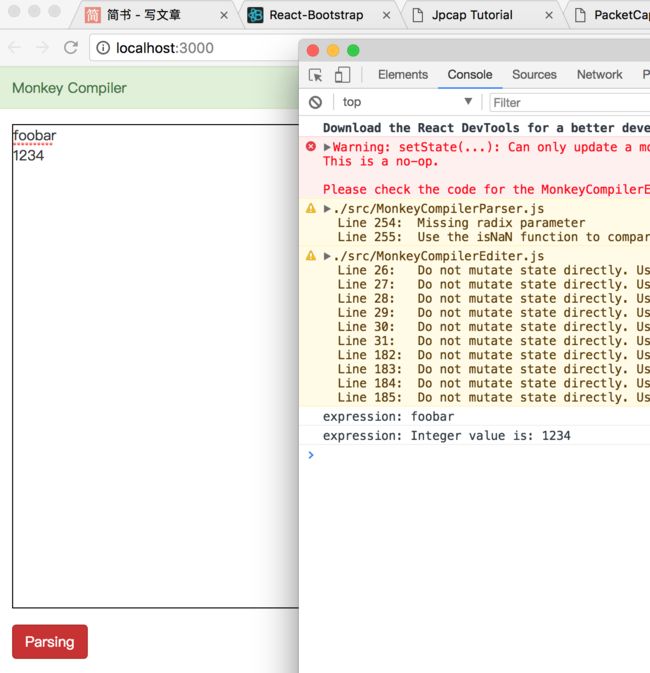
上面代码完成后,我们在编辑框中输入变量和数字字符串,点击解析按钮后,解析结果如下:
从上图所示结果来看,我们的解析器已经能轻松的处理算术表达式中的两种简单情况,也就是变量和数字,当然算术表达式最复杂的还是带有运算符和函数调用的情况,接下来我们会就这些复杂情况的处理做深入探讨。
普拉特解析法的特点是通过查表来获得对当前token的解析函数,程序事先配置好各种情况下的解析方式,运行时就可以根据具体遇到的token迅速从表中获得解析函数去执行即可。从这一节看来,普拉特解析法似乎只处理了两种非常简单的算术表达式情况,在后面的章节中,我们会看到该方法在解析非常复杂的表达式,例如含有多层括号,函数间套调用,运算符的优先级和前缀中序变化等棘手情况时,普拉特分析法将产生巨大的解析威力。
更多技术信息,包括操作系统,编译器,面试算法,机器学习,人工智能,请关照我的公众号: