R语言采用多元回归建模的基本步骤
前言:本次建模过程是基于RedHat6.8或者CentOS6.8,R3.1.2,Rstudio-server
关于R3.1.2,Rstudio-server的整个配置,原始数据(已经脱敏处理,不涉及泄密,如有侵权,请随时联系)以及本分析的源码均放置在GitHub上,通过click here访问
数据导入:
#install essential packages
install.packages("rJava",dependencies=TRUE)
install.packages("xlsx",dependencies=TRUE)
install.packages("corrplot",dependencies=TRUE)
install.packages("leaps",dependencies=TRUE)
install.packages("lmtest",dependencies=TRUE)
library(rJava)
#setting workstation
setwd("/home/steven/workstation")
#source data loaded
library(xlsx)
src <- read.xlsx("/usr/local/workstation/test.xls",1,encoding="UTF-8")数据处理:
#drop columns that is useless
src <- src[,-c(1)]
src <- src[,c(1:6,8:10,7)]
#1、description statistic
attach(src)
names(src)
mean=sapply(src,mean)
max=sapply(src,max)
min=sapply(src,min)
median=sapply(src,median)
sd=sapply(src,sd)
cbind(mean,max,min,median,sd)建立回归模型步骤:
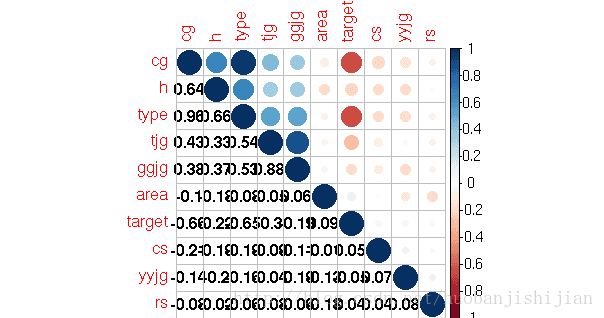
#1、参数全部默认情况下的相关系数图
#混合方法之上三角为圆形,下三角为黑色数字
library(corrplot)
corr <- cor(src[,1:10])
corrplot(corr = corr,order="AOE",type="upper",tl.pos="tp")
corrplot(corr = corr,add=TRUE, type="lower",
method="number",order="AOE", col="black",
diag=FALSE,tl.pos="n", cl.pos="n")输出结果如下:
1. mean max min median sd
rs 1211.924227 14000.0000 10.0000 980.00000 1.595892e+03
cs 1.168495 6.0000 0.0000 1.00000 1.471799e+00
area 7.045862 11.0000 1.0000 7.00000 3.168251e+00
type 1.588235 2.0000 1.0000 2.00000 4.923985e-01
cg 2.251246 3.0000 1.0000 3.00000 9.289564e-01
h 1.395813 2.0000 1.0000 1.00000 4.892685e-01
tjg 7843.554775 8454.1182 6909.4630 8092.36154 3.942006e+02
ggjg 14147.557328 16600.0000 11700.0000 14600.00000 1.015608e+03
yyjg 94.608809 106.6788 86.6484 95.00923 3.467941e+00
target 29893.998495 145085.0000 4.9000 27700.00000 1.939754e+04#1、参数全部默认情况下的相关系数图
#混合方法之上三角为圆形,下三角为黑色数字
library(corrplot)
corr <- cor(src[,1:10])
corrplot(corr = corr,order="AOE",type="upper",tl.pos="tp")
corrplot(corr = corr,add=TRUE, type="lower",
method="number",order="AOE", col="black",
diag=FALSE,tl.pos="n", cl.pos="n")#2.画相关图选择回归方程的形式
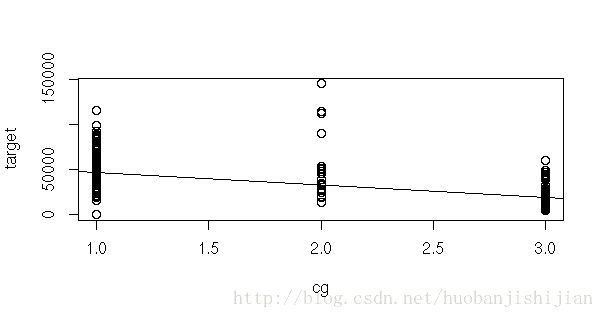
plot(target~cg);abline(lm(target~cg))
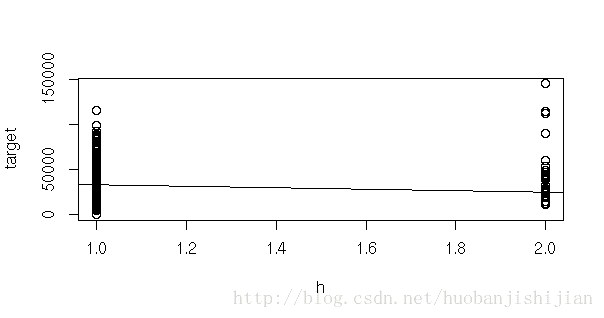
plot(target~h);abline(lm(target~h))
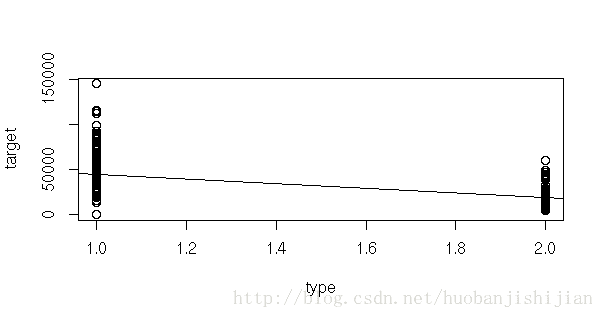
plot(target~type);abline(lm(target~type))
plot(target~tjg);abline(lm(target~tjg))
plot(target~ggjg);abline(lm(target~ggjg))
plot(target~area);abline(lm(target~area))
plot(target~cs);abline(lm(target~cs))
plot(target~yyjg);abline(lm(target~yyjg))
plot(target~rs);abline(lm(target~rs))#3.do regression and check results
dim(src)[1]
lm.test<-lm(target~rs+cs+area+type+cg+h+tjg+ggjg+yyjg,data=src)
summary(lm.test)结果如下:
Residuals:
Min 1Q Median 3Q Max
-45689 -8172 -999 5979 90290
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.678e+04 1.487e+04 6.507 1.22e-10 ***
rs 9.556e-02 2.643e-01 0.362 0.71777
cs -5.617e+02 2.887e+02 -1.946 0.05195 .
area 2.137e+02 1.390e+02 1.537 0.12463
type -3.414e+04 4.309e+03 -7.923 6.20e-15 ***
cg -1.846e+03 2.136e+03 -0.864 0.38776
h 1.336e+04 1.158e+03 11.535 < 2e-16 ***
tjg -1.198e+01 2.460e+00 -4.868 1.31e-06 ***
ggjg 7.148e+00 1.079e+00 6.625 5.66e-11 ***
yyjg -3.731e+02 1.280e+02 -2.916 0.00363 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 12980 on 993 degrees of freedom
Multiple R-squared: 0.5564, Adjusted R-squared: 0.5523
F-statistic: 138.4 on 9 and 993 DF, p-value: < 2.2e-16
#4.delete variable which is not significant(rs,area)
lm.test<-lm(target~cs+type+cg+h+tjg+ggjg+yyjg,data=src)
summary(lm.test)Residuals:
Min 1Q Median 3Q Max
-46131 -8655 -1038 5716 91466
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 101636.162 14537.438 6.991 4.99e-12 ***
cs -572.037 288.600 -1.982 0.04774 *
type -34143.617 4296.236 -7.947 5.14e-15 ***
cg -1815.420 2127.549 -0.853 0.39370
h 12995.825 1132.191 11.478 < 2e-16 ***
tjg -12.728 2.411 -5.279 1.59e-07 ***
ggjg 7.474 1.058 7.068 2.96e-12 ***
yyjg -389.096 127.090 -3.062 0.00226 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 12980 on 995 degrees of freedom
Multiple R-squared: 0.5553, Adjusted R-squared: 0.5522
F-statistic: 177.5 on 7 and 995 DF, p-value: < 2.2e-16#4.1.use residual analysis delete outlier points
plot(lm.test,which=1:4)
src = src[-c(12,765,788,790),]
dim(src)[1]得到的四个图依次为:
4.1普通残差与拟合值的残差图
4.2正态QQ的残差图(若残差是来自正态总体分布的样本,则QQ图中的点应该在一条直线上)
4.3标准化残差开方与拟合值的残差图(对于近似服从正态分布的标准化残差,应该有95%的样本点落在[-2,2]的区间内。这也是判断异常点的直观方法)
4.4cook统计量的残差图(cook统计量值越大的点越可能是异常值,但具体阀值是多少较难判别)
从图中可见,12,765,788,790三个样本存在异常,需要剔除。
Residuals:
Min 1Q Median 3Q Max
-46131 -8655 -1038 5716 91466
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 101636.162 14537.438 6.991 4.99e-12 ***
cs -572.037 288.600 -1.982 0.04774 *
type -34143.617 4296.236 -7.947 5.14e-15 ***
cg -1815.420 2127.549 -0.853 0.39370
h 12995.825 1132.191 11.478 < 2e-16 ***
tjg -12.728 2.411 -5.279 1.59e-07 ***
ggjg 7.474 1.058 7.068 2.96e-12 ***
yyjg -389.096 127.090 -3.062 0.00226 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 12980 on 995 degrees of freedom
Multiple R-squared: 0.5553, Adjusted R-squared: 0.5522
F-statistic: 177.5 on 7 and 995 DF, p-value: < 2.2e-16#5.异方差检验
#5.1GQtest,H0(误差平方与自变量,自变量的平方和其交叉相都不相关),
#p值很小时拒绝H0,认为上诉公式有相关性,存在异方差
src.test<-residuals(lm.test)
library(lmtest)
gqtest(lm.test)
#5.2BPtest,H0(同方差),p值很小时认为存在异方差
bptest(lm.test)结果如下:
Goldfeld-Quandt test
data: lm.test
GQ = 1.841, df1 = 494, df2 = 493, p-value = 8.865e-12
---------
studentized Breusch-Pagan test
data: lm.test
BP = 93.9696, df = 7, p-value < 2.2e-16两个检验的p值都很小时认为存在异方差,需要修正异方差
#6.修正异方差
#修正的方法选择FGLS即可行广义最小二乘
#6.1修正步骤
#6.1.1将y对xi求回归,算出res--u
#6.1.2计算log(u^2)
#6.1.3做log(u^2)对xi的辅助回归 log(u^2),得到拟合函数g=b0+b1x1+..+b2x2
#6.1.4计算拟合权数1/h=1/exp(g),并以此做wls估计
lm.test2<-lm(log(resid(lm.test)^2)~cs+type+cg+h+tjg+ggjg+yyjg,data=src)
lm.test3<-lm(target~cs+type+cg+h+tjg+ggjg+yyjg,weights=1/exp(fitted(lm.test2)),data=src)
summary(lm.test3)结果如下:
Weighted Residuals:
Min 1Q Median 3Q Max
-5.0707 -1.3281 -0.2952 1.0471 9.3937
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 61648.563 13382.003 4.607 4.62e-06 ***
cs -320.525 153.174 -2.093 0.0366 *
type -26556.135 4766.749 -5.571 3.26e-08 ***
cg -4653.887 2430.178 -1.915 0.0558 .
h 11107.677 692.499 16.040 < 2e-16 ***
tjg -14.767 2.224 -6.638 5.20e-11 ***
ggjg 7.919 1.049 7.548 9.96e-14 ***
yyjg 97.193 133.864 0.726 0.4680
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.868 on 995 degrees of freedom
Multiple R-squared: 0.7178, Adjusted R-squared: 0.7159
F-statistic: 361.6 on 7 and 995 DF, p-value: < 2.2e-16#7.1计算解释变量相关稀疏矩阵的条件数k,k<100多重共线性程度很小,100<k<1000较强,>1000严重
src[1:9]
XX<-cor(src[1:9])
kappa(XX)结果如下:
[1] 160.9175K>100 and K<1000,说明共线性较强,接下来找出共线性强的变量
$values
[1] 3.4192494 1.3030312 1.1563047 0.9199288 0.9041041 0.7562702 0.4205589 0.1011783
[9] 0.0193744
$vectors
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] -0.05733512 -0.501899822 0.2026552 -0.50588080 0.52056535 -0.417997886
[2,] -0.14763837 0.007109461 0.4116265 -0.46530338 -0.75069812 -0.163284493
[3,] -0.05138859 0.665302345 -0.1293286 -0.01422961 0.11408507 -0.699971313
[4,] 0.49655847 -0.112090220 -0.1278988 0.02167963 -0.16337262 -0.239671005
[5,] 0.46448785 -0.167719865 -0.2352263 0.06705893 -0.20715145 -0.265202906
[6,] 0.40186335 -0.218262940 -0.2471633 -0.09210826 -0.11794142 0.001433268
[7,] 0.40615453 0.174700538 0.5215318 0.06040287 0.12878909 0.132238544
[8,] 0.40635458 0.274603051 0.4469450 -0.07777933 0.20683789 0.127659436
[9,] -0.13555751 -0.333404886 0.4101634 0.71008868 -0.09781406 -0.383530067
[,7] [,8] [,9]
[1,] -0.02888533 0.034061964 -0.010937600
[2,] 0.03865752 -0.008224625 -0.020908812
[3,] 0.16651561 0.084133996 0.004735702
[4,] -0.30629410 -0.209415519 0.708684433
[5,] -0.36523446 0.094446587 -0.663876582
[6,] 0.83587224 0.093172922 0.004206256
[7,] -0.04882043 0.695383719 0.094120334
[8,] 0.10362759 -0.660605287 -0.217813589
[9,] 0.17586069 -0.101388052 -0.011659019#8.修正多重共线性---逐步回归法
#ps2:step中可进行参数设置:
#direction=c("both","forward","backward")来选择逐步回归
#的方向,默认both,forward时逐渐增加解释变两个数,backward则相反。
step(lm.test)结果如下:
Start: AIC=19007.25
target ~ cs + type + cg + h + tjg + ggjg + yyjg
Df Sum of Sq RSS AIC
- cg 1 1.2269e+08 1.6778e+11 19006
1.6766e+11 19007
- cs 1 6.6200e+08 1.6832e+11 19009
- yyjg 1 1.5794e+09 1.6924e+11 19015
- tjg 1 4.6960e+09 1.7235e+11 19033
- ggjg 1 8.4171e+09 1.7608e+11 19054
- type 1 1.0643e+10 1.7830e+11 19067
- h 1 2.2201e+10 1.8986e+11 19130
Step: AIC=19005.98
target ~ cs + type + h + tjg + ggjg + yyjg
Df Sum of Sq RSS AIC
1.6778e+11 19006
- cs 1 5.9084e+08 1.6837e+11 19008
- yyjg 1 1.5277e+09 1.6931e+11 19013
- tjg 1 5.3779e+09 1.7316e+11 19036
- ggjg 1 1.2972e+10 1.8075e+11 19079
- h 1 2.2083e+10 1.8986e+11 19128
- type 1 1.5438e+11 3.2216e+11 19658
Call:
lm(formula = target ~ cs + type + h + tjg + ggjg + yyjg, data = src)
Coefficients:
(Intercept) cs type h tjg ggjg
99781.026 -533.902 -37652.525 12909.485 -13.222 7.941
yyjg
-381.819 所以最终入选的变量是:formula = target ~ cs + type + h + tjg + ggjg + yyjg