数据科学 案例13 聚类与K-mean聚类（代码）

15 聚类与K-mean聚类

import os
# import numpy as np
import pandas as pd
# import matplotlib.pyplot as plt

15.1 层次聚类

1、手动测试主成分数量

# 1、引入数据
model_data = pd.read_csv(r'.\data\cities_10.csv',encoding='gbk')
model_data.head()

	AREA	X1	X2	X3	X4	X5	X6	X7	X8	X9
0	辽宁	5458.2	13000	1376.2	2258.4	1315.9	529.0	2258.4	123.7	399.7
1	山东	10550.0	11643	3502.5	3851.0	2288.7	1070.7	3181.9	211.1	610.2
2	河北	6076.6	9047	1406.7	2092.6	1161.6	597.1	1968.3	45.9	302.3
3	天津	2022.6	22068	822.8	960.0	703.7	361.9	941.4	115.7	171.8
4	江苏	10636.3	14397	3536.3	3967.2	2320.0	1141.3	3215.8	384.7	643.7

data = model_data.loc[ :,'X1':]
data.head()

	X1	X2	X3	X4	X5	X6	X7	X8	X9
0	5458.2	13000	1376.2	2258.4	1315.9	529.0	2258.4	123.7	399.7
1	10550.0	11643	3502.5	3851.0	2288.7	1070.7	3181.9	211.1	610.2
2	6076.6	9047	1406.7	2092.6	1161.6	597.1	1968.3	45.9	302.3
3	2022.6	22068	822.8	960.0	703.7	361.9	941.4	115.7	171.8
4	10636.3	14397	3536.3	3967.2	2320.0	1141.3	3215.8	384.7	643.7

#2、查看相关系数矩阵，判定做变量降维的必要性（非必须）
corr_matrix = data.corr(method='pearson')
#corr_matrix = corr_matrix.abs()
corr_matrix

	X1	X2	X3	X4	X5	X6	X7	X8	X9
X1	1.000000	-0.094292	0.966506	0.979238	0.922984	0.921680	0.941148	0.637458	0.825568
X2	-0.094292	1.000000	0.112726	0.074167	0.214052	0.093483	-0.042776	0.081195	0.273145
X3	0.966506	0.112726	1.000000	0.985373	0.963159	0.939194	0.935196	0.704714	0.898016
X4	0.979238	0.074167	0.985373	1.000000	0.972862	0.939720	0.962267	0.713890	0.913364
X5	0.922984	0.214052	0.963159	0.972862	1.000000	0.971337	0.937109	0.716722	0.934549
X6	0.921680	0.093483	0.939194	0.939720	0.971337	1.000000	0.897127	0.624294	0.848004
X7	0.941148	-0.042776	0.935196	0.962267	0.937109	0.897127	1.000000	0.836272	0.928692
X8	0.637458	0.081195	0.704714	0.713890	0.716722	0.624294	0.836272	1.000000	0.881528
X9	0.825568	0.273145	0.898016	0.913364	0.934549	0.848004	0.928692	0.881528	1.000000

# 3、做主成分之前，进行中心标准化
from sklearn import preprocessing
data = preprocessing.scale(data)

# 4、使用sklearn的主成分分析，用于判断保留主成分的数量
from sklearn.decomposition import PCA
'''说明：1、第一次的n_components参数应该设的大一点
   说明：2、观察explained_variance_ratio_和explained_variance_的取值变化，建议explained_variance_ratio_累积大于0.85，explained_variance_需要保留的最后一个主成分大于0.8，
'''
pca=PCA(n_components=3)
newData=pca.fit(data)
print(pca.explained_variance_)
print(pca.explained_variance_ratio_)

[8.01129553 1.22149318 0.60792399]
[0.80112955 0.12214932 0.0607924 ]

2、根据主成分分析确定需要保留的主成分数量，进行因子分析

#1、导入包，并对输入的数据进行主成分提取。为保险起见，data需要进行中心标准化
from fa_kit import FactorAnalysis
from fa_kit import plotting as fa_plotting
fa = FactorAnalysis.load_data_samples(
        data,
        preproc_demean=True,
        preproc_scale=True
        )
fa.extract_components()

# 2、设定提取主成分的方式。默认为“broken_stick”方法，建议使用“top_n”法
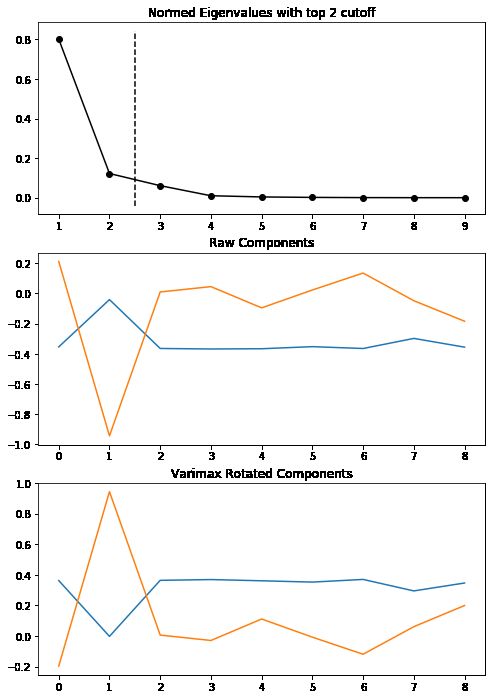
fa.find_comps_to_retain(method='top_n',num_keep=2)

array([0, 1], dtype=int64)

# 3、通过最大方差法进行因子旋转
fa.rotate_components(method='varimax')
fa_plotting.graph_summary(fa)
# 说明：可以通过第三张图观看每个因子在每个变量上的权重，权重越高，代表性越强

# 4、获取因子得分
pd.DataFrame(fa.comps["rot"])

	0	1
0	0.362880	-0.196047
1	-0.001947	0.943648
2	0.364222	0.006565
3	0.369255	-0.028775
4	0.361258	0.111596
5	0.352799	-0.007144
6	0.370140	-0.118691
7	0.295099	0.061400
8	0.346765	0.199650

import numpy as np
fas = pd.DataFrame(fa.comps["rot"])
data = pd.DataFrame(data)
score = pd.DataFrame(np.dot(data, fas))
score

	0	1
0	-1.174241	-0.364178
1	2.095775	-0.654819
2	-1.399899	-0.870629
3	-3.265185	0.698849
4	2.386557	-0.337666
5	0.163901	2.802894
6	1.209012	0.048116
7	-2.084500	-0.322173
8	5.501759	0.105138
9	-3.433179	-1.105531

3、根据因子得分进行数据分析

a=score.rename(columns={0: "Gross", 1: "Avg"})
citi10_fa=model_data.join(a)
citi10_fa

	AREA	X1	X2	X3	X4	X5	X6	X7	X8	X9	Gross	Avg
0	辽宁	5458.2	13000	1376.2	2258.4	1315.9	529.0	2258.4	123.7	399.7	-1.174241	-0.364178
1	山东	10550.0	11643	3502.5	3851.0	2288.7	1070.7	3181.9	211.1	610.2	2.095775	-0.654819
2	河北	6076.6	9047	1406.7	2092.6	1161.6	597.1	1968.3	45.9	302.3	-1.399899	-0.870629
3	天津	2022.6	22068	822.8	960.0	703.7	361.9	941.4	115.7	171.8	-3.265185	0.698849
4	江苏	10636.3	14397	3536.3	3967.2	2320.0	1141.3	3215.8	384.7	643.7	2.386557	-0.337666
5	上海	5408.8	40627	2196.2	2755.8	1970.2	779.3	2035.2	320.5	709.0	0.163901	2.802894
6	浙江	7670.0	16570	2356.5	3065.0	2296.6	1180.6	2877.5	294.2	566.9	1.209012	0.048116
7	福建	4682.0	13510	1047.1	1859.0	964.5	397.9	1663.3	173.7	272.9	-2.084500	-0.322173
8	广东	11769.7	15030	4224.6	4793.6	3022.9	1275.5	5013.6	1843.7	1201.6	5.501759	0.105138
9	广西	2455.4	5062	367.0	995.7	542.2	352.7	1025.5	15.1	186.7	-3.433179	-1.105531

citi10_fa.to_csv("citi10_fa.csv")

#如遇中文显示问题可加入以下代码
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题

import matplotlib.pyplot as plt
x=citi10_fa['Gross']   #总的
y=citi10_fa['Avg']     #人均的
label=citi10_fa['AREA']
plt.scatter(x, y)
for a,b,l in zip(x,y,label):
    plt.text(a, b+0.1, '%s.' % l, ha='center', va= 'bottom',fontsize=14)

plt.show()

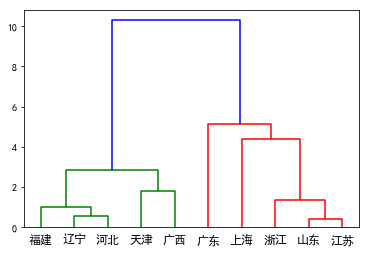
import scipy.cluster.hierarchy as sch
#1. 层次聚类
#生成点与点之间的距离矩阵,这里用的欧氏距离:
disMat = sch.distance.pdist(citi10_fa[['Gross','Avg']],'euclidean') 
#进行层次聚类:
Z=sch.linkage(disMat,method='ward') 
#将层级聚类结果以树状图表示出来并保存为plot_dendrogram.png
P=sch.dendrogram(Z,labels=['辽宁','山东','河北','天津','江苏','上海','浙江','福建','广东','广西'])#label的顺序要注意
plt.savefig('plot_dendrogram1.png')

15.2 K-means聚类分析

15.2.1 测试主成分数量、因子分析

# ### 第一步：手动测试主成分数量
# - 1、引入数据
import pandas as pd
model_data = pd.read_csv(r".\data\profile_bank.csv")
data = model_data.loc[ :,'CNT_TBM':'CNT_CSC']
data.head()

	CNT_TBM	CNT_ATM	CNT_POS	CNT_CSC
0	34	3	3	9
1	44	17	5	18
2	122	26	32	36
3	42	3	6	1
4	20	15	2	2

# - 2、查看相关系数矩阵，判定做变量降维的必要性（非必须）

corr_matrix = data.corr(method='pearson')
#corr_matrix = corr_matrix.abs()
corr_matrix

	CNT_TBM	CNT_ATM	CNT_POS	CNT_CSC
CNT_TBM	1.000000	0.055648	0.083624	0.198835
CNT_ATM	0.055648	1.000000	0.341161	0.242106
CNT_POS	0.083624	0.341161	1.000000	0.234055
CNT_CSC	0.198835	0.242106	0.234055	1.000000

# - 3、做主成分之前，进行中心标准化

from sklearn import preprocessing
data = preprocessing.scale(data)

# - 4、使用sklearn的主成分分析，用于判断保留主成分的数量

from sklearn.decomposition import PCA
'''说明：1、第一次的n_components参数应该设的大一点
   说明：2、观察explained_variance_ratio_和explained_variance_的取值变化，建议explained_variance_ratio_累积大于0.85，explained_variance_需要保留的最后一个主成分大于0.8，
'''
pca=PCA(n_components=4)
newData=pca.fit(data)
print(pca.explained_variance_)
print(pca.explained_variance_ratio_)

[1.60786876 1.00252275 0.7339482  0.65570029]
[0.40196317 0.25062818 0.18348521 0.16392343]

'''通过主成分在每个变量上的权重的绝对值大小，确定每个主成分的代表性
'''
pd.DataFrame(pca.components_).T

	0	1	2	3
0	0.303020	0.834245	0.445132	0.118622
1	0.555131	-0.377566	0.135542	0.728630
2	0.559520	-0.315486	0.386716	-0.661708
3	0.535673	0.248894	-0.796201	-0.131035

# ### 第二步：根据主成分分析确定需要保留的主成分数量，进行因子分析

# - 1、导入包，并对输入的数据进行主成分提取。为保险起见，data需要进行中心标准化

from fa_kit import FactorAnalysis
from fa_kit import plotting as fa_plotting
fa = FactorAnalysis.load_data_samples(
        data,
        preproc_demean=True,
        preproc_scale=True
        )
fa.extract_components()

# - 2、设定提取主成分的方式。默认为“broken_stick”方法，建议使用“top_n”法

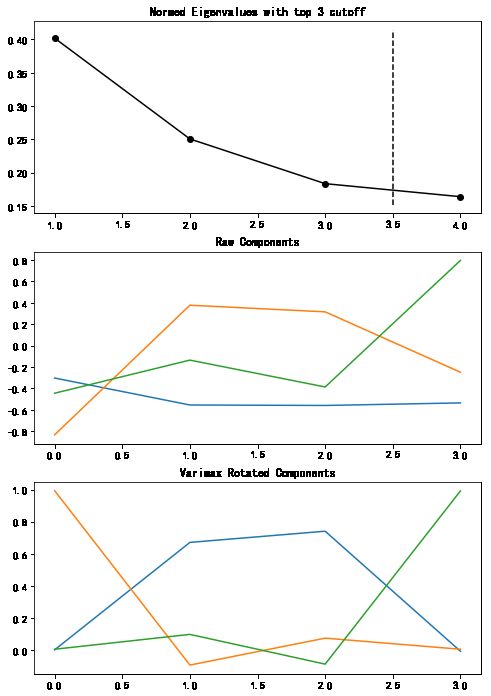
fa.find_comps_to_retain(method='top_n',num_keep=3)

array([0, 1, 2], dtype=int64)

# - 3、通过最大方差法进行因子旋转

fa.rotate_components(method='varimax')
fa_plotting.graph_summary(fa)
# - 说明：可以通过第三张图观看每个因子在每个变量上的权重，权重越高，代表性越强

# - 4、获取因子得分

pd.DataFrame(fa.comps["rot"])

import numpy as np
fas = pd.DataFrame(fa.comps["rot"])
data = pd.DataFrame(data)
score = pd.DataFrame(np.dot(data, fas))

# ### 第三步：根据因子得分进行数据分析

fa_scores=score.rename(columns={0: "ATM_POS", 1: "TBM", 2: "CSC"})
fa_scores.head()

	ATM_POS	TBM	CSC
0	-0.852354	-0.294938	0.143935
1	-0.333078	-0.244334	0.939343
2	0.918067	0.593787	2.349496
3	-0.741847	-0.210507	-0.521592
4	-0.499703	-0.492714	-0.367629

15.2.1、使用因子得分进行k-means聚类

1、k-means聚类的第一种方式：不进行变量分布的正态转换–用于寻找异常值

# - 1、查看变量的偏度

var = ["ATM_POS","TBM","CSC"]
skew_var = {}
for i in var:
    skew_var[i]=abs(fa_scores[i].skew())
    skew=pd.Series(skew_var).sort_values(ascending=False)
skew

TBM        51.881233
CSC         6.093417
ATM_POS     2.097633
dtype: float64

# - 2、进行k-means聚类

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3) #MiniBatchKMeans()分批处理
#kmeans = cluster.KMeans(n_clusters=3, init='random', n_init=1)
result=kmeans.fit(fa_scores)
#print(result)
result

KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
       n_clusters=3, n_init=10, n_jobs=None, precompute_distances='auto',
       random_state=None, tol=0.0001, verbose=0)

# - 3、对分类结果进行解读

model_data_l=model_data.join(pd.DataFrame(result.labels_))
model_data_l=model_data_l.rename(columns={0: "clustor"})
model_data_l.head()

	ID	CNT_TBM	CNT_ATM	CNT_POS	CNT_CSC	CNT_TOT	clustor
0	41360	34	3	3	9	49	0
1	52094	44	17	5	18	84	0
2	57340	122	26	32	36	216	1
3	76885	42	3	6	1	52	0
4	89150	20	15	2	2	39	0

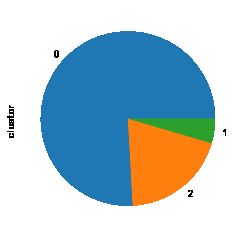
import matplotlib
get_ipython().magic('matplotlib inline')
model_data_l.clustor.value_counts().plot(kind = 'pie') 

2、k-means聚类的第二种方式：进行变量分布的正态转换–用于客户细分

# - 1、进行变量分布的正态转换

import numpy as np
from sklearn import preprocessing
quantile_transformer = preprocessing.QuantileTransformer(output_distribution='normal', random_state=0)
fa_scores_trans=quantile_transformer.fit_transform(fa_scores)
fa_scores_trans=pd.DataFrame(fa_scores_trans)
fa_scores_trans=fa_scores_trans.rename(columns={0: "ATM_POS", 1: "TBM", 2: "CSC"})
fa_scores_trans.head()

	ATM_POS	TBM	CSC
0	-0.501859	-0.265036	0.770485
1	0.097673	-0.154031	1.316637
2	0.952085	1.168354	1.845934
3	-0.333179	-0.084688	-1.780166
4	-0.071278	-0.888898	-0.066404

var = ["ATM_POS","TBM","CSC"]
skew_var = {}
for i in var:
    skew_var[i]=abs(fa_scores_trans[i].skew())
    skew=pd.Series(skew_var).sort_values(ascending=False)
skew

CSC        5.400815e-04
ATM_POS    4.822917e-04
TBM        2.196784e-07
dtype: float64

# - 2、进行k-means聚类

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=4) #MiniBatchKMeans()分批处理
#kmeans = cluster.KMeans(n_clusters=3, init='random', n_init=1)
result=kmeans.fit(fa_scores_trans)
print(result)

KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
       n_clusters=4, n_init=10, n_jobs=None, precompute_distances='auto',
       random_state=None, tol=0.0001, verbose=0)

# - 3、对分类结果进行解读

model_data_l=model_data.join(pd.DataFrame(result.labels_))
model_data_l=model_data_l.rename(columns={0: "clustor"})
model_data_l.head()

	ID	CNT_TBM	CNT_ATM	CNT_POS	CNT_CSC	CNT_TOT	clustor
0	41360	34	3	3	9	49	3
1	52094	44	17	5	18	84	0
2	57340	122	26	32	36	216	0
3	76885	42	3	6	1	52	1
4	89150	20	15	2	2	39	3

import matplotlib
get_ipython().magic('matplotlib inline')
model_data_l.clustor.value_counts().plot(kind = 'pie') 

data1 = model_data.loc[ :,'CNT_TBM':'CNT_CSC']

from sklearn import tree

clf = tree.DecisionTreeClassifier(criterion='gini', max_depth=2, min_samples_split=100, min_samples_leaf=100, random_state=12345)  # 当前支持计算信息增益和GINI
clf.fit(data1, result.labels_)
# print(result.labels_ == model_data_l.clustor )

DecisionTreeClassifier(ccp_alpha=0.0, class_weight=None, criterion='gini',
                       max_depth=2, max_features=None, max_leaf_nodes=None,
                       min_impurity_decrease=0.0, min_impurity_split=None,
                       min_samples_leaf=100, min_samples_split=100,
                       min_weight_fraction_leaf=0.0, presort='deprecated',
                       random_state=12345, splitter='best')

import pydotplus
from IPython.display import Image
import sklearn.tree as tree

dot_data = tree.export_graphviz(clf, 
                                out_file=None, 
                                feature_names=data1.columns,  
                                class_names=['0','1','2','3'],
                                filled=True) 

graph = pydotplus.graph_from_dot_data(dot_data)  
Image(graph.create_png())