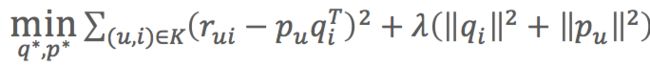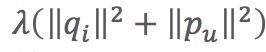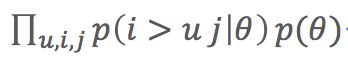推荐系统三十六式：矩阵分解 学习总结

• 作者：jliang

  https://blog.csdn.net/jliang3

 

1.重点归纳

1）评分预测问题只是很典型，其实并不大众，毕竟在实际的应用中，评分数据很难收集到；与之相对的另一类问题是行为预测才是平民级推荐问题。在真正的推荐系统的实际应用中，评分预测实际上场景很少，而且数据很少，相比预测评分，预测“用户会对物品干出什么事”会更加有效。

2）矩阵分解

（1）矩阵分解常用的方法是SVD（奇异值分解）把用户和物品都映射到一个k维空间中，分解后的矩阵实质上就是得到了每个用户和每个物品的隐因子向量，拿着物品和用户两个向量计算点积就是推荐分数了。

（2）为了解决不同用户的评分标准不一样，以及某些物品存在一些铁粉这样的问题，引入了偏置信息，包括：全局评分、物品评分偏置、用户评分偏置：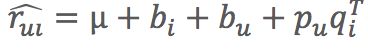

（3）为了解决用户显式反馈比较少，引入用户隐式反馈以及用户属性等信息，SVD中结合用户隐式反馈行为和属性的模型叫SVD++。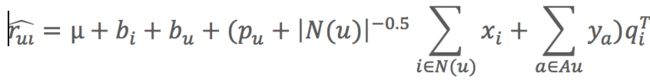

（4）考虑时间因素

• 对评分按照时间加权，让久远的评分更趋近平均值
• 对评分时间划分区间，不同时间区间内分别学习隐因子向量，使用时按照区间使用对应的因因子向量来计算
• 对特殊的期间，如节日、周末等训练对应的隐因子向量

3）矩阵分解要将用户物品评分矩阵分解成两个小矩阵，一个代表用户偏好的用户隐因子向量组成，另一个矩阵代表物品语义主题的隐因子向量组成，两者是一一对应的，用户的兴趣就表现在物品的语义维度上。

（1）矩阵分解时经常使用交替最小二乘进行求解，先固定其中一个矩阵，利用线性代数对另外一个矩阵进行求解；然后再反过来另一个矩阵，再对第一个矩阵求解；反复求解直至误差很小。

（2）在对隐式反馈进行预测时，只有明确的某类已经干过的正类（One-Class问题），负类数据靠采样获取（随机均匀采样或按照热门程度采样），使用加权交替最小二乘（Weighted-ALS）进行求解

• 如果用户对物品无隐式反馈则认为评分是0
• 如果用户对物品有至少一次隐式反馈则认为评分为1，次数作为该评分的置信度
• 目标函数：
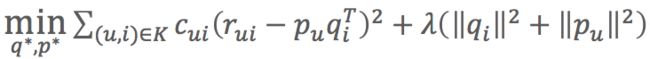
  • 相对原来的目标函数多了cui参数
  • cui=1+αC，超参数α默认值为40可以得到差不多的效果，C就是次数

（3）让用户和物品的隐因子向量两两相乘，计算点积就可以得到所有推荐的结果。但是在数据量巨大时实际复杂度很高，一般采取以下两种方式来解决

• 利用一些专门设计的数据结构存储所有物品的隐因子向量，从而实现通过一个用户向量可以反馈最相似的K个物品。
• 拿物品的隐因子向量做聚类，海量的物品会减少为少量的聚类。然后再逐一计算用户和每个聚类中心的推荐分数，给用户推荐物品就变成了给用户推荐聚类。

4）贝叶斯个性化排序（Bayesian Personalized Ranking，BPR）直接预测物品两两之间的相对顺序（pair-wise问题）

（1）BPR构造样本

         BPR提出要关心物品之间对于用户的相对顺序，构造的样本是：用户、物品1、物品2、两个物品相对顺序

• 如果物品1消费过的，而物品不是，那么相对顺序取值1，是正样本
• 如果物品1和物品2刚好相反，则是负样本
• 样本中不包含其他情况：物品1和物品2都是消费过的，或者都是没消费过的

（2）最大化交叉熵就是BPR目标函数，最大化目标函数就能得到分解后的矩阵参数。

（3）训练方法

         BPR使用了一个介于批量下降法和随机梯度下降法的训练方法，结合重复抽样的梯度下降：

• 从全量样本中有放回地随机一部分样本
• 用这部分样本，采用随机梯度下降优化目标函数，更新模型参数
• 重复步骤，直到满足停止条件

 

2.那些在Netflix Prize中大放异彩的推荐算法

1）近邻模型的问题

（1）物品之间存在相关性，信息量并不随着向量维度增加而线性增加。

（2）矩阵元素系数，计算结果不稳定，增减一个向量维度，导致近邻结果差异很大的情况存在。

矩阵分解可以解决这两个问题。矩阵分解就是把原来的大矩阵，近似分解成两个小矩阵的乘积，在实际推荐计算时直接使用两个小矩阵。

2）基础的SVD算法

（1）矩阵分解常用的方法是SVD（奇异值分解），由于向量是稀疏的，无法直接进行奇异值分解，在推荐算法中使用的并不是正统的奇异值分解，而是一个伪奇异值分解。

（2）矩阵分解就是把用户和物品都映射到一个k维空间中，这个k维空间不是我们直接看到的，也不具有很好的解释性，每个维度也没有名字，所以常常称为隐因子，代表隐藏在直观的矩阵数据下面。

（3）损失函数：

• 控制模型的偏差。用分解后的矩阵预测分数，要和实际的用户评分之间误差越小越好。
• 控制模型的方差。得到的隐因子向量要越简单越好，以控制模型的方差。

（4）得到分解后的矩阵实质上就是得到了每个用户和每个物品的隐因子向量，拿着物品和用户两个向量计算点积就是推荐分数了。

3）SVD算法增加偏置信息

（1）原因：有一些用户给出偏高的评分（比如标准宽松的用户），有些物品也会收到偏高的评分（如目标观众为铁粉的电影），甚至有可能整个平台的全局评分就偏高。

（2）增加偏置：一个用户给一个物品的评分由四部分相加

• 
• μ：全局平均分
• bi：物品评分偏置，即：物品的评分-全局评分
• bu：用户评分偏置，即：用户平均评分-全局评分
• ：用户和物品之间的兴趣偏好

（3）损失函数：

• 与基本的SVD相比，增加了两个参数要学习：用户偏置和物品偏置

4）SVD算法增加历史行为

（1）原因：用户评分比较少，显示反馈比隐式反馈少，使用隐式反馈弥补这个问题；另外再考虑一些用户的个人属性（如性别等）加入模型来弥补冷启动的不足。SVD中结合用户隐式反馈行为和属性的模型叫SVD++。

（2）隐式反馈加入

• 除了加速评分矩阵中的物品有一个隐因子向量外，用户有过行为的物品集合也都有一个隐因子向量，维度时一样的。
• 用户操作过的物品隐因子向量加起来，用来表达用户的兴趣偏好。

（3）用户属性加入

• 全都转成0-1型的特征后，对每个特征也假设都存在一个同样维度的隐因子向量。
• 一个用户的所有属性对应的隐因子向量相加，也代表了他的一些偏好。

（4）用户向量：

• 与之前的SVD相比，只是增加了两个学习参数:x和y。一个是隐式反馈的物品向量，另外一个用户属性的向量。

5）考虑时间因素

（1）对评分按照时间加权，让久远的评分更趋近平均值

（2）对评分时间划分区间，不同时间区间内分别学习隐因子向量，使用时按照区间使用对应的因因子向量来计算

（3）对特殊的期间，如节日、周末等训练对应的隐因子向量

3.Facebook是怎么为十亿人互相推荐好友的

1）矩阵分解要将用户物品评分矩阵分解成两个小矩阵，一个代表用户偏好的用户隐因子向量组成，另一个矩阵代表物品语义主题的隐因子向量组成，两者是一一对应的，用户的兴趣就表现在物品的语义维度上。两个小矩阵相乘得到的矩阵的维度与用户物品评分矩阵一模一样。

（1）这两个矩阵的特点：

• 每个用户对应一个k维向量，每个物品也对应一个k维向量
• 两个矩阵相乘后，就得到了任何一个用户对任何一个物品的预测评分

（2）目标函数的优化方法常用有两个：随机梯度下降（SGD）和交替最小二乘法（ALS）。实际应用中交替最小二乘法更常用一些。

2）交替最小二乘原理

（1）我们的任务是找到两个矩阵P和Q，让它们相乘后约等于原矩阵R：

（2）最小二乘的步骤：

• 初始化随机矩阵Q里面的所有元素
• 把Q矩阵当做已知，直接用线性代数的方法求得矩阵P
• 得到矩阵P后，把P当做已知，求解矩阵Q
• 上面两个步骤交替进行，一直到误差可以接受为止

（3）ALS好处

• 在假设已知其中一个矩阵求解另一个时，要优化的参数很容易并行化
• 在不那么稀疏的数据集合上，ALS通常比随机梯度下降更快

3）隐式反馈

（1）矩阵分解算法是为解决评分预测问题而生的，然而实际应用中用户的隐式反馈数据更多。

One-Class问题：如果把预测用户行为看成二分类问题，猜用户会不会做某件事实际上收集到的数据只有明确的一类（用户干了某事），而用户“不干”某件事的数据没有明确表达。

（2）交替最小二乘法改进版：加权交替最小二乘（Weighted-ALS）

行为的次数是对行为的置信度反应，也就是所谓的加权。

（3）加权交替最小二乘法对待隐式反馈的方式

• 如果用户对物品无隐式反馈则认为评分是0
• 如果用户对物品有至少一次隐式反馈则认为评分为1，次数作为该评分的置信度
• 目标函数：
  • 相对原来的目标函数多了cui参数
  • cui=1+αC，超参数α默认值为40可以得到差不多的效果，C就是次数

（4）取值为0的数据非常多，不能一股脑使用所有缺失值（评分为0的数据）作为负类，矩阵分解的初心是要填充这些值。解决这个问题的方法是负样本采样，挑一部分缺失值作为负类样本。挑选方法：

• 随机均匀采样和正类别一样多（不是很靠谱）
• 按照物品的热门程度采样（在实践中经过了检验），一个越热门的物品，用户越可能知道它的存在，这时候还没有反馈，可能它才是真正的负样本。

4）推荐计算

让用户和物品的隐因子向量两两相乘，计算点积就可以得到所有推荐的结果。但是在数据量巨大时实际复杂度很高，Fackbook提出两个办法来得到真正的推荐结果：

• 利用一些专门设计的数据结构存储所有物品的隐因子向量，从而实现通过一个用户向量可以反馈最相似的K个物品。
  • Facebook开源的Faiss，类似开源实现还有Annoy、KGraph、NMSLIB。
  • 如果需要动态增加新的物品向量到索引中，推荐使用Faiss，否则推荐使用KGraph或NMSLIB
• 拿物品的隐因子向量做聚类，海量的物品会减少为少量的聚类。然后再逐一计算用户和每个聚类中心的推荐分数，给用户推荐物品就变成了给用户推荐聚类。

4.如果关注排序效果，那么这个模型可以帮到你

1）矩阵分解本质上是在预测用户对一个物品的偏好程度。针对单个用户对单个物品的偏好程度进行预测，得到结果后再排序的问题叫point-wise。直接预测物品两两之间的相对顺序问题叫pair-wise。

（1）point-wise模型的问题：只能收集到正样本，没有负样本，于是认为缺失值就是负样本，再以预测误差为评判标准去逼近这些样本。

（2）更直接的推荐模型是能够较好地为用户排列出更好的物品相对顺序，而非精确评分。

2）贝叶斯个性化排序（Bayesian Personalized Ranking，BPR）

（1）评价模型预测精准程度可以使用AUC，ACU这个值在数学上等价于：模型把关心的那一类样本排在其他样本前面的概率。最大是1，0.5就是随机排序，0就是全部排错。

（2）AUC计算

• 用模型给样本计算推荐分数。样本都是用户和物品的一对一，同时还包含了有无反馈的标识
• 得到打过分的样本，每条样本保留两个信息：分数和是否消费过（1为消费过的正样本，0为没有消费过的负样本）
• 按照分数对样本重新排序，降序排序
• 给每一个样本赋一个排序值，第一位r1=n，第二位r2=n-1；如果几个样本分数一样，需要将其排序值调整为他们的平均值
• 按照下面公式计算得到的AUC值

• 正样本M个，其他样本N个，M×N为两类样本相对排序总的组合可能性
• 分子：第一名排序值r1，它在排序上不但比过了所有负样本，而且比过了自己以外的正样本。

3）BPR做法

（1）样本构造方法

（2）模型目标函数

（3）模型学习框架

4）BPR构造样本

（1）BPR提出要关心物品之间对于用户的相对顺序，构造的样本是：用户、物品1、物品2、两个物品相对顺序

（2）两个物品的相对顺序

• 如果物品1消费过的，而物品不是，那么相对顺序取值1，是正样本
• 如果物品1和物品2刚好相反，则是负样本
• 样本中不包含其他情况：物品1和物品2都是消费过的，或者都是没消费过的

5）BPR目标函数

（1）物品1和物品2的似然概率是最大化交叉熵：

         Xu12表示用户u，物品1和物品2的矩阵分解预测分数差，然后再用sigmoid把分数压缩到0-1之间。

（2）通常还要加入L2正则项，正则项其实认为模型参数还有个先验概率，所以BPR名字中的贝叶斯的由来。BPR认为模型的先验概率符合正态分布。

（3）目标函数：

• 最大化目标函数就能得到分解后的矩阵参数，其中θ是分解后的矩阵参数
• 这个目标函数化简和变形后就和AUC当初目标函数非常相似了，所以BPR模型作者宣称该模型是为AUC而生的。

6）训练方法

（1）BPR使用了一个介于批量下降法和随机梯度下降法的训练方法，结合重复抽样的梯度下降：

• 从全量样本中有放回地随机一部分样本
• 用这部分样本，采用随机梯度下降优化目标函数，更新模型参数
• 重复步骤，直到满足停止条件